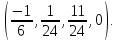а₁₁α₁+а₁₂ α ₂+…+а_1nα_n=b₁

а₂₁α₁+а₂₁ α ₂+…+а_2nα_n=b₂

_{. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .}

а_ί1α₁+а_ί2 α ₂+…+а_ίnα_n=b_ί (3.5)

_{. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .}

а_k1α₁+а_k2 α ₂+…+а_knα_n=b_k

_{. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .}

a_m1α₁+а_m2 α ₂+…+а_mnα_n=b_m

Совершим элементарное преобразование III типа системой (3.I).т. е. прибавим к ί-ому уравнению k-ое, умноженное на число . Мы получаемсистему:

а₁₁x₁+a₁₂x₂+ . . .+a_1nx_n=b₁

. . . . . . . . . . . . . . . . . . . . .

(a_ί1+ca_k1)x+. . .+(a_ίn+ca_kn)x_n=b_ί+cb_k

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (3.6)

a_k1x₁+a_k2x₂+ . . .+a_knx_n=b_k

. . . . . . . . . . . . . . . . . . . . . .

a_m1x₁+a_m2x₂+ . . . +a_mnx_n=b_m

Подставляя набор чисел (α₁, α₂, . . .,α_n) в систему (3.6) получаем:

a₁₁α₁ +. . . + a_1nα_n = b₁

.. . . . . . . . . . . . . . . . . . . . . .

(a_ί1+ca_k1)α+ . . . +(a_ίn+ca_kn)α_n = пока не знаем что

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (3.7)

a_k1α₁ + . . . + a_knα_n = b_k

. . . . . . . . . . . . . . . . . . . . . . . .

a_m1α₁ + . . . + a_mnα_n = b_m

ибо все остальные уравнения кроме ί –ого в системе (3.6) совпадают с уравнениями системы (3.І). Левую же часть ί-ого уравнения системы (3.6) после подстановки в нее набора (α₁, . . . ,α_n) можно записать как:

(a_ί1α₁+ . . . +a_ίnα_n)+ca_k1α₁+ . . .+ca_knα_n=(a_ί1α₁+ . . .+a_ίnα₁)+c(a_k1α₁+ . . .+a_knα_n)=b_ί+cb_k

Значит (α₁, α₂, . . . ,α_n) является решениеми ί –ого уравнения системы (3.6).

Таким образом мы показали, что всякое решение системы (3.І) является решением системы (3.6). Покажем , что имеет место и обратное: Пусть (β₁, β₂, . . . ,β_n) – произвольное решение системы(3.6). Значит, имеет место набор верных числовых равенств:

а₁₁β₁+a₁₂β₂+ . . .+a_1nβ_n=b₁

. . . . . . . . . . . . . . . . . . . . .

(a_ί1+ca_k1)β₁+. . .+(a_ίn+ca_kn)β_n=b_ί+cb_k

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . (3.8)

a_k1β₁+a_k2β₂+ . . .+a_knβ_n=b_k

. . . . . . . . . . . . . . . . . . . . . .

a_m1β₁+a_m2β₂+ . . . +a_mnβ_n=b_m

Так как (3.8) совокупность верных числовых равенств, то вычтем из ί-ого равенства k-ое, умноженное на с. Получим :

а₁₁β₁ +. . .+ a_1nβ_n = b₁

. . . . . . . . . . . . . . . .

aί1β1 +. . .+ a_ίnβn = b_ί

. . . . . . . . . . . . . . . . . . (3.9)

a_k1β₁ +. . .+ a_knβ_n = b_k

. . . . . . . . . . . . . . . . . . .

a_m1β₁ +. . . + a_mnβ_n = b_m

а это и означает, что всякое решение системы (3.6) является решением системы (3.І).

Итак, мы уже знаем те преобразования системы линейных уравнений, которые приводят ее к системе, эквивалентной исходной. Наша задача описать, как путем последовательного применения элементарных преобразований можно перейти от заданной системы к системе более простого вида. Эту задачу решил Гаусс и мы переходим к изложению метода Гаусса.

§4. Метод гаусса последовательного исключения неизвестных

Пусть нам дана произвольная система линейных уравнений:

a₁₁x₁+a₁₂x₂ + . . .+ a_1nx_n = b₁

a₂₁x₁+a₂₂x₂ + . . . + a_2nx_n = b₂

. . . . . . . . . . . . . . . . . . . . . . . . (4.I)

a_m1x₁+a_m2x₂+ . . . +a_mnx_n = b_m

где а_ij, b_k (i=1,2,....,n; j=1,2,...,m; k=1,2,…,m) принадлежат некоторому числовому полю.

Без ограничения общности можем предложить, что а₁₁0, ибо если а₁₁ = 0, то применив элементарное преобразование І типа, поменяем местами первое уравнение с таким j –м что а_j10. Если все а_k1 = 0 (k=1,2, …,m) то просто нет смысла говорить о переменной х₁ . Нам нужно из 2-го, 3-го и т. д. m-го уравнения исключить переменную х₁. Повторим процесс исключения переменной х₁ в случае системы 2-х линейных уравнений с двумя неизвестными, рассмотренный ранее. Для этого умножим первое уравнение на –и прибавим его ко второму, умножим первое уравнение на –и прибавим к 3-му уравнению и т. Д. – умножим первое уравнение на –и прибавим к последнему. Мы совершилиm-1 элементарное преобразование третьего типа и пришли к системе, эквивалентной исходной:

a₁₁x₁+a₁₂x₂ + . . .+ a_1nx_n = b₁

a’₂₂x₂ + . . . + a’_2nx_n = b’₂

. . . . . . . . . . . . . . . . . . . (4.2)

a’_m2x₂+ . . . +a’_mnx_n = b’_m

В (4.2) х_k – неизвестное с наименьшим номером, которое входит в какое-нибудь уравнение, не считая первого. k может быть больше двух, т. к. может оказаться, что в процессе исключения х₁исключилась и переменная х₂,…,х_к-1 . Оставив I уравнение без изменения, ко всем остальным применим те же рассуждения, что и ранее и исключаем из 3-го, 4-го,. . . ,m-го уравнений переменную х_к . Будем применять этот процесс до тих пор, пока возможно. В конце концов система примет вид:

+ . . . +

. . . . . . . . . . . . . . . . . . . . . . . (4.3)

. . . . . . . . .

Здесь (что можно записать одним условием , ибо в поле нет делителей нуля ( см. [2], стр. 185, [I], стр.279), Может оказатися, что и поэтому уравнений вида в системе (4.3) не будет. Систему вида (4.3) называют системой ступенчатого ( или трапецеидального) вида.

Так мы показали, что всякая система линейных уравнений (4.I) эквивалентна системе ступенчатого вида. Так как мы пришли к системе, эквивалентной исходной, то достаточно вопрос о совместности системы (4.I) и вопрос о числе решений системы (4.I) исследовать для систем ступенчатого вида.

1. СОВМЕСТНОСТЬ СИСТЕМЫ (4.3).

Если система (4.3) содержит уравнение виде , где, то эта система несовместна, т.к. уравнениенельзя удовлетворить никаким значениям для переменных. Если таких уравнений в системе (4.3) нет, то система совместна. В самом деле, объявимглавными неизвестными ( мы это делаем потому, что коэффициентыотличны от нуля). Остальные переменные назовем свободными. Придавая свободным переменным произвольные значения и подставляем их в систему (4.3) снизу вверх, найдем наконец. Таким образом значения для главных неизвестных определяются однозначно при любых значениях для свободных неизвестных, ибо нам приходится каждый разрешить уравнениеI степени вида .

Значит, для совместной системы линейных уравнений необходимо и достаточно, чтобы после приведения ее к ступенчатому виду в ней не оказалось уравнений вида .

2. Если в совместной системе есть свободные переменные (), то система неопределенная и имеет, как нетрудно видеть, безконечно много решений, ибо мы бесконечным числом способов можем составлять из элементов числового поля (содержащем бесконечно много элементов) числовые наборы для свободных переменных.

Если же у совместной системе свободных неизвестных нет и все неизвестные главные, то система линейных уравнений является определенной. Это имеет место тогда , когда в ступенчатом виде . Болем подробно метод Гаусса см. [I], стр. 15 – 23,( [2], стр. 23-33).

Отметим одно наблюдение. Каждой системе линейных уравнений ( 4.I) соответствует таблица коэффициентов этой системы вида:

(4.4)

називаемая матрицей. Здесь . Вообще как вы знаете, матрицы изучаются и отдельно, независимо от систем линейных уравнений. Матрица вида (4.4) называется матрицей коэффициентов системы (4.I). В этой матрице есть строки:

(4.5)

- первая строка матрицы

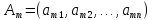- вторая строка матрицы

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

- m-ая строка матрицы

и есть столбцы

(4.6)

Если мы к матрице А припишем -ым столбе свободных членовсистемы ( 4.I), то получим так называемую расширенную матрицу системы ( 4.I):

(4.7)

Над строчками и столбцами матрицы А вводим элементарные преобразования типов I, II и III точно так же, как и в определенных 3.3, 3.4 и 3,5 с заменой слова «уравнение» словом «строка» («столбец»). Приводя систему (4.I) к ступенчатому виду (4.3) ми одновременно получаем такой факт:

Всякую матрицу с помощью элементарных преобразований можно привести к ступенчатому виду.

Рассмотрим ряд примеров на примере метода Гаусса.

ПРИМЕР 4.1. Выяснить, совместна ли система линейных уравнений и если да, то найти все ее решения.

(4.8)

РЕШЕНИЕ. Как мы ранее отмечали, всякой системе линейных уравнений соответствует расширенная матрица вида ( 4.7). Так вот при практическом решении системы линейных уравнений методом Гаусса удобнее выписать расширенную матрицу системы, опустив неизвестные , и выполнить элементарные преобразования только строк расширенной матрицы. Мы имеем из (4.8)

(4.9)

Первое уравнение :строку матрицы (4.9) умножим на -2 и прибавим ко второму, умножим на -3 и прибавим к третьему. Такой процедурой исключим и придем к расширенной матрице

(4.10)

Затем второе уравнение в (4.10) вычтем из третьего, исключив одновременно. Получим:

(4.11)

Мы полностью реализовали метод Гаусса. Записав по расширенной матрице (4.11) систему имеем:

Получили равенство , что невозможно, поэтому система (4.8) несовместна.

ПРИМЕР 4.2. Выяснить, совместна ли система линейных уравнений, и если да, то найти все ее решения:

(4.12)

РЕШЕНИЕ. Мы имеем:

(4.13)

Здесь мы сначала первое уравнение вычли из всех остальных, а затем второе прибавили к третьему , второе умножили на 2 и прибавили к четвертому уравнению.

В (4.13) не получили противоречного уравнения вида ,а потому система совместна. Из (4.13) имеем:

(4.14)

Главными неизвестными являются и, свободными-и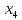. Теперь по ступенькам ступенчатого вида (4.14) снизу вверх. Из второго уравнения получаем:

(4.15)

Из первого уравнения (4.14), подставив вместоправую часть (4.15), находим:

Таким образом мы можем написать систему линейных уравнений: (4.16)

элементарную исходной, в которой выделены свободные неизвестные и главные независимые, которые можно найти через свободные.

Совокупность решений вида(4.16) называется общим решением системы.

Придавая свободным неизвестным произвольные действительные значения, мы получим все бесконечное множество решений неопределенной системы (4.12). ( у нас а потом совместная система (4.12) имеет бесконечно много решений). Положив, например,получаем частное решение:

ЗАМЕЧАНИЕ. Вы, наверное, уже заметили, как удобно, если и коэффициенты, получающиеся при главных неизвестных, тоже малы или равны 0. Этого всегда можно добиться. Прежде чем решать систему по методу Гаусса, нужно внимательно посмотреть на элементы. Если среди них есть 1, например,то совершив элементарное преобразованиеI типа, то есть переставить 1-ое и k-ое уравнения, выведем на место “11” число 1.

ПРИМЕР 4.3. Пользуясь методом Гаусса, решить систему:

(4.17)

РЕШЕНИЕ. Составляем расширенную матрицу:

Переставим первое и третье уравнения местами:

Вычтем из третьего уравнения второе, умножим второе на -4 и прибавим к четвертому:

Умножим четвертое уравнение на 2 и прибавим ко второму:

Умножим третье уравнение на -19 и прибавим к четвертому

Система совместна и имеет единственное решение, т.к. Запишем систему, эквивалентную системе (4.17):

(4.18)

Поднимаясь по ступенькам снизу вверх, в (4.18), получаем:

Решением системы является набор действительных чисел:

ЗАМЕЧАНИЕ. Если среди элементов нет единицы, ее можно “сделать”, применяя элементарное преобразования к уравнениям системы.

ПРИМЕР4.4. Применяя метод Гаусса, исследовать совместна ли система, и если да, найти все ее решения.

(4.19)

РЕШЕНИЕ. Поменяем местами первое и второе уравнение:

Здесь мы из третьего уравнения вычли первое. Вычтем из первого уравнения второе:

Здесь мы сначала ко второму уравнению прибавили первое, умноженное на -2, разделим третье, умноженное на 4. Теперь умножая второе на 2 и прибавляя к третьему, окончательно получим:

или

Система линейных уравнений совместна и имеет бесконечно много решений, ибо

Общее решение системы (4.19):

Частное решение системы (4.19):