Обратный ход метода Гаусса: преобразование полученной ступенчатой матрицы к матрице, в первых n столбцах которой содержится единичная матрица , последний,(n+1)-й, столбец этой матрицы содержит решение системы.

Система линейных уравненийимеет вид:

a₁₁ x₁ + a₁₂ x₂     +... + a_1n x_n = b₁,

a₂₁ x₁ + a₂₂ x₂    +... + a_2n x_n = b₂,                          (5.1)

...     ...     ...     ...

a_m1 x₁ + a_m1 x₂ +... + a_mn x_n = b_m.

Здесь а_{i j}и b_i(i =; j =) - заданные, а x_j- неизвестные действительные числа. Используя понятие произведения матриц, можно переписать систему (5.1) в виде:

AX = B,                                                             (5.2)

где A = (а_{i j}) - матрица, состоящая из коэффициентов при неизвестных системы (5.1), которая называетсяматрицей системы, X = (x₁, x₂,..., x_n)^T, B = (b₁, b₂,..., b_m)^T- векторы-столбцы, составленные соответственно из неизвестных x_jи из свободных членов b_i.

Упорядоченная совокупность nвещественных чисел (c₁, c₂,..., c_n) называетсярешением системы(5.1), если в результате подстановки этих чисел вместо соответствующих переменных x₁, x₂,..., x_n каждое уравнение системы обратится в арифметическое тождество; другими словами, если существует вектор C= (c₁, c₂,..., c_n)^Tтакой, что AC = B.

Система (5.1) называется совместной,илиразрешимой, если она имеет по крайней мере одно решение. Система называетсянесовместной,илинеразрешимой, если она не имеет решений.

Матрица

,

образованная путем приписывания справа к матрице A столбца свободных членов, называется расширенной матрицей системы.

Вопрос о совместности системы (5.1) решается следующей теоремой.

Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранги матриц A исовпадают, т.е. r(A) = r() = r.

Для множества М решений системы (5.1) имеются три возможности:

1) M = ∅(в этом случае система несовместна);

2) M состоит из одного элемента, т.е. система имеет единственное решение (в этом случае система называется определенной);

3) M состоит более чем из одного элемента (тогда система называется неопределенной). В третьем случае система (5.1) имеет бесчисленное множество решений.

Система имеет единственное решение только в том случае, когда r(A) = n. При этом число уравнений - не меньше числа неизвестных (m≥n); если m>n, то m-n уравнений являются следствиями остальных. Если 0<r<n, то система является неопределенной.

Для решения произвольной системы линейных уравнений нужно уметь решать системы, в которых число уравнений равно числу неизвестных, - так называемые системы крамеровского типа:

a₁₁ x₁ + a₁₂ x₂ +... + a_1n x_n = b₁,

a₂₁ x₁ + a₂₂ x₂ +... + a_2n x_n = b₂,                                        (5.3)

...     ...     ...     ...     ...     ...

a_n1 x₁ + a_n1 x₂ +... + a_nn x_n = b_n.

Системы (5.3) решаются одним из следующих способов: 1) методом Гаусса, или методом исключения неизвестных; 2) по формулам Крамера; 3) матричным методом.

Рассмотрим систему mлинейных алгебраических уравнений относительноnнеизвестныхx₁ , x₂ , ..., x_n:

Решениемсистемы называется совокупностьnзначений неизвестных

x₁=x'₁ , x₂ =x'₂ , ..., x_n=x'_n ,

при подстановке которых все уравнения системы обращаются в тождества.

Система линейных уравнений может быть записана в матричном виде:

где A— матрица системы, b— правая часть,x— искомое решение,A_p—расширенная матрицасистемы:

.

Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения —несовместной.

Однородной системой линейных уравнений называется система, правая часть которой равна нулю:

Матричный вид однородной системы: Ax=0.

Однородная система в с е г д а  с о в м е с т н а, поскольку любая однородная линейная система имеет по крайней мере одно решение:

x₁=0 , x₂=0 , ..., x_n=0.

Если однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется тривиально совместной. Если же однородная система имеет более одного решения, то среди них есть и ненулевые и в этом случае система называетсянетривиально совместной.

Доказано, что при m=nдля нетривиальной совместности системынеобходимо и достаточно, чтобыопределительматрицы системы был равен нулю.

 Применив к матрице системы алгоритм гауссова исключения, приведем матрицу системы к ступенчатому виду

.

Число rненулевых строк в ступенчатой форме матрицы называетсярангом матрицы, обозначаем r=rg(A)  илиr=Rg(A).

Справедливо следующее утверждение.

Для того, чтобы однородная система была нетривиально совместна, необходимо и достаточно, чтобы ранг rматрицы системы был меньше числа неизвестныхn.

Если однородная система нетривиально совместна, то она имеет бесконечное множество решений, причем линейная комбинация любых решений системы тоже является ее решением. Доказано, что среди бесконечного множества решений однородной системы можно выделить ровно n-rлинейно независимых решений. Совокупность n-rлинейно независимых решений однородной системы называетсяфундаментальной системой решений.Любое решение системы линейно выражается через фундаментальную систему. Таким образом, если ранг r матрицыAоднородной линейной системыAx=0меньше числа неизвестныхnи векторыe₁ , e₂ , ..., e_n-rобразуют ее фундаментальную систему решений (Ae_i =0, i=1,2, ..., n-r), то любое решениеxсистемыAx=0можно записать в виде

x=c₁ e₁ + c₂ e₂ +  ... + c_n-r e_n-r ,

где c₁ , c₂ , ..., c_n-r— произвольные постоянные. Записанное выражение называетсяобщим решением однородной системы.

Исследоватьоднородную систему   — значит установить, является ли она нетривиально совместной, и если является, то найти фундаментальную систему решений и записать выражение для общего решения системы.

Исследуем однородную систему методом Гаусса.

Пусть

матрица исследуемой однородной системы, ранг которой r< n.

Такая матрица приводится Гауссовым исключением к ступенчатому виду

.

Соответствующая эквивалентная система имеет вид

Отсюда легко получить выражения для переменных x₁ , x₂ , ..., x_rчерез x_r+1 , x_r+2 , ..., x_n. Переменныеx₁ , x₂ , ..., x_rназываютбазисными переменными, а переменныеx_r+1 , x_r+2 , ..., x_n—свободными переменными.

Перенеся свободные переменные в правую часть, получим формулы

которые определяют общее решение системы.

Положим последовательно значения свободных переменных равными

и вычислим соответствующие значения базисных переменных. Полученные n-rрешений линейно независимы и, следовательно, образуют фундаментальную систему решений исследуемой однородной системы:

Рассмотрим неоднородную системуmлинейных алгебраических уравнений относительноnнеизвестныхx₁ , x₂ , ..., x_n:

В отличие от однородной системы, эта система совместна не всегда. Справедливо следующее утверждение (теорема Кронекера-Капелли).

Для того, чтобы неоднородная система линейных алгебраических уравнений была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы системы совпадал с рангом матрицы системы. 

Исследоватьнеоднородную систему — это значит установить, является ли она совместной, и если является — найти выражение для общего решения системы.

Исследуем неоднородную систему методом Гаусса.

Пусть

расширенная матрица исследуемой системы, ранг которой rравен рангу матрицы системы иr< n.

Такая матрица приводится Гауссовым исключением к ступенчатому виду

.

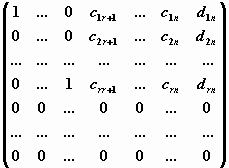Соответствующая эквивалентная система имеет вид

Отсюда легко получить выражения базисных переменных x₁ , x₂ , ..., x_rчерез свободные переменныеx_r+1 , x_r+2 , ..., x_n. Формулы

определяют общее решение системы. Положив свободные переменные равными нулю, x_r+1 =0, x_r+2 =0, ..., x_n=0, и вычислив соответствующие значения базисных переменных, получимчастное решениеисследуемой системы

x₁ =d₁ , x₂ =d₂ , ..., x_r=d_r , x_r+1 =0, x_r+2 =0, ..., x_n=0.

Билет 4

Определение. Линейным пространством или векторным пространством над полемназывается множество с двумя операциями:

-- сложение , где;

-- умножение на скаляр , где, для которых выполнены условия:

коммутативность сложения: для любых,

ассоциативность сложения: для любых,

существования нейтрального элемента :для любого,

существования противоположного элемента :для любого,

для любых и,

для любого ,

для любых и,

для любых и.

Следствие. Нейтральный элемент единственен.

Противоположный элемент единственен.

.

.

.

тогда и только тогда, когда или.

Определение. Пусть дана система векторов , где.Линейная комбинация векторов системы -- это выражение вида , где. Линейная комбинацияназываетсятривиальной, если . Система векторовназываетсялинейно зависимой, если существует такая нетривиальная линейная комбинация , что. Система векторовназываетсялинейно независимой, если из равенства следует, что.

Утверждение.[Свойства линейной зависимости] Система, состоящая из одного вектора, линейно зависима тогда и только тогда, когда.

Если , то системалинейно зависима тогда и только тогда, когда один из векторов системы линейно выражается через остальные.

Если подсистема системылинейно зависима, то и вся система линейно зависима.

Система, содержащая нулевой вектор, линейно зависима.

Если система линейно независима, а системалинейно зависима, то векторлинейно выражается через вектора.

Лемма.[Основная лемма о линейной зависимости и независимости системы] Пусть система векторов линейно независима, а каждый ее вектор линейно выражается через векторы системы. Тогда.

Определение. Система называетсямаксимальной линейно независимой системой в линейном пространстве , если любое расширениеэтой системы линейно зависимо.

Следствие. Если идве максимальные линейно независимые системы в, то.

Определение. Пространство называется-мерным ( ), если весть максимальная линейно независимая система, состоящая извекторов. Если такой подсистемы нет ни для какого, то. Если, то по определению

Определение. Система векторов называетсябазисом линейного пространства , если каждый векторединственным образом записывается в виде линейной комбинации,.

Предложение. Система векторов является базисом в пространстветогда и только тогда, когдаявляется максимальной линейно независимой системой в.

Предложение. Пусть ---мерное векторное пространство,. Тогда всуществует хотя бы один базис. Более того, каждая линейно независимая системаможет быть дополнена до некоторого базиса.

Предложение. Система является базисом в-мерном векторном пространстветогда и только тогда, когда эта система линейно независима и.

Предложение. Система является базисом в-мерном векторном пространстветогда и только тогда, когдаи каждый векторлинейно выражается через эти векторы.

Рассмотрим арифметическое пространство , состоящее из множества строк,. Вектора(наместе стоит) -- образуют базис.

Следствие. В пространстве система,, является базисом тогда и только тогда, когда

Матрица перехода

Координаты вектора в базисе-- это коэффициенты разложения векторапо базису, где.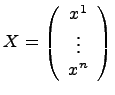

Пусть даны два базиса и, причем,,.

Определение.Матрица

-ый столбец которой составлен из координат вектора в базисе, называетсяматрицей переходаот базисак. Имеем.

Лемма.Пусть-- базис, аи-- матрицы размеранад полем, причем. Тогда.

Теорема.Матрица переходаот базисакневырождена.

Для любого базисаи любой невырожденной квадратной матрицыпорядкасуществует и при том единственный базисс матрицей перехода, т.е..

Теорема.Если-- матрица перехода от базисак, то для любого векторасправедливо равенство, гдеи-- столбцы координат векторав базисахисоответственно, т.е..

Определение.Биекциялинейного пространстванад полемна линейное пространствонад полемназываетсяизоморфизмомлинейных пространств, еслидля любых векторови.

Следствие.Справедливы равенства,и. Если системалинейна независима, то систематоже линейна независима. Отображение-- изоморфизм.

Определение.Два линейных пространства называютсяизоморфными, если существует изоморфизм одного пространства на другое.

Теорема.Два конечномерных пространства над полемизоморфны тогда и только тогда, когда.

Следствие.Любое-мерное векторное пространствоизоморфно. Отображениеопределено так:.

Билет 5

Определение. Непустое подмножество линейного пространстваназываетсяподпространством, если для любых векторови.

Замечание. В любом пространстве содержится нулевое подпространство (самое маленькое). Пространствосамое большое. Если, тои. Еслии, то.

Теорема. Пусть иподпространства конечномерного пространства, причем. Тогдаи из равенства размерностей следует равенство подпространств.

Определение. Пусть ,.Линейной оболочкой системыназывается множество значений всевозможных линейных комбинаций, где. Линейная оболочка пустого множества -- это нулевое подпространство.

Теорема. Линейная оболочкаявляется подпространством пространства.

Всякое подпространство конечномерного линейного пространстваявляется линейной оболочкой некоторой системы,.

Определение. Две системы векторов иназываютсяэквивалентными, если каждый вектор второй системы линейно выражается через вектора первой системы и наоборот.

Определение. Рангом системыназывается число векторов максимальной линейно независимой подсистемы.

Теорема. Если две системыиэквивалентны, то.

.

Если -- базис в пространстве, торавен рангу матрицы, столбцами которой являются столбцы координат векторовв базисе.

Пусть ,, -- подпространства линейного пространства. Тогда их пересечениеявляется подпространством в. Действительно, оно непусто (есть нулевой элемент); если, тодля любого, и, следовательно, при любыхимеем, т.е..

Рассмотрим множество . Множествоявляется подпространство в. Действительно, оно непусто (есть нулевой элемент); если, то, и, следовательно, при любыхимеем.

Теорема. Пусть и-- подпространства конечномерного пространства. Тогда.

Определение. Линейное пространство являетсяпрямой суммой своих подпространств , если каждый вектордопускает, причем единственное, разложение в сумму, где. Вектораназываютсяпроекциями вектора на подпространствовдоль подпространств. Пишут.

Теорема. Пусть -- конечномерное пространство и, где-- подпространства в. Тогда следующие свойства равносильны:

;

для любых базисов пространства,, системаявляется базисом в;

для некоторых базисов пространства,, системаявляется базисом в;

;

для любого выполнено, где.

Билет 6

Определение. Пусть и-- два линейных пространства над полем. Отображениеназываетсялинейным, если для любыхи.

Замечание. Если , то получим определение линейной функции.

Если , то линейное отображениеназываетсялинейным оператором.

Пример.

Нулевой оператор: для любого.

Тождественный оператор: для любого.

Пусть . Положим. Тогда-- линейный оператор.

Определим формулойприипри.

Пусть -- пространство вещественных многочленов. Определимформулой.

Пусть . Определимформулой, где.

Определение. Ядром линейного отображенияназывается множество.

Образом линейного отображенияназывается множествосуществует  такойчто.

Утверждение. Ядро и образявляются подпространствами в.

Теорема. Пусть -- линейное отображение конечномерного пространствав пространство. Тогда.

Теорема. Пусть -- базис пространстванад полем. Тогда для любых векторов,, линейного пространстванадсуществует, причем единственное, линейное отображениесо свойством.

Определение. Матрицей линейного операторав базиселинейного пространства называется квадратная матрицапорядка, столбцы которой составлены из координат образовбазисных векторовв базисе, т.е.

Следствие. Пусть -- базис пространства. Тогда для любой квадратной матрицы порядкасуществует, причем единственный, линейный операторс матрицейв этом базисе.

Теорема. Пусть -- матрица линейного операторав базисе. Тогда для любого векторастолбец координатего образав базисенаходится по формуле, где-- столбец координат вектора.

Лемма. Пусть и-- матрицы размера. Если для любого столбцавысотысправедливо равенство, то.

Теорема. Пусть и-- матрицы линейного операторав базисахисоответственно. Тогда, где-- матрица перехода от базисак.

Определение. Определителем линейного оператораназывается определитель матрицы оператора в каком-то базисе. Оператор называетсявырожденным, если .

Лемма. Определитель операторане зависит от выбора базиса.

Определение. Рангом линейного оператораназывается рангего матрицы в каком-то базисе.

Замечание. .

Лемма. При умножении матрицы справа или слева на невырожденную матрицу рангматрицыне меняется.

Из этой леммы получаем

Теорема. Ранг операторане зависит от выбора базиса.

Лемма. Пусть и-- два линейных оператора. Тогда отображение

, определенное по формуле для любого вектора, является линейным оператором;

, определенное по формуле для любого вектора, является линейным оператором;

, , определенное по формуледля любого вектора, является линейным оператором.

Верно равенство .

Теорема. Пусть и-- два линейных оператора c матрицамиисоответственно в базисе. Тогда

матрицей оператора в базисеявляется матрица;

матрицей оператора в базисеявляется матрица;

матрицей оператора ,, в базисеявляется матрица.

Определение. Оператор является обратным для, если, где-- тождественный оператор.

Определение. Оператор называется невырожденным, если его матрица в некотором базисе невырождена.

Теорема. Следующие свойства линейного оператора на-мерном линейном пространстве равносильны.

Оператор невырожден.

Оператор обратим.

Для всякого базиса вобразысоставляют базис в.

Для некоторого базиса вобразысоставляют базис в.

Оператор сюръективен.

Ядро тривиально, т.е..

Оператор инъективен.

Билет 7