227

50a0 125a1 365a2 151,125a0 365a1 1175a2 405,

365a0 1175a1 4025a2 1237.

Решив систему уравнений по методу Крамера, найдем значения коэффициентов уравнения регрессии a0 = 1,424; a1 = 0,799; a0 = - 0,055 и запишем уравнение регрессии

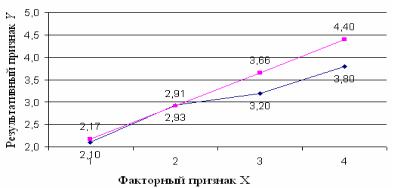
Графики эмпирической и теоретической линий регрессии представлены на рисунке 6.49.

Рисунок 6.49 – Эмпирическая и теоретическая линии регрессии

6.8.4 Множественная регрессия

Чаще всего, при эксплуатации вооружения КВ один результативный признак, описывающая показатель эксплуатационного свойства или процесса, зависит не от одного факторного признака, а от нескольких. Пусть, например, случайная величина Y зависит от X1, X2, …, Xn, где n - число факторных признаков. В этом случае для изучения связи между переменными используют видоизмененный метод, применяемый для двух случайных величин, и уравнение связи составляют между случайной величиной Y и n переменными x.

Для простоты рассуждений условимся считать, что связь линейная и форма связи определяется следующим уравнение регрессии

где x1, x2, …, xn – переменные (факторные признаки);

a0, a1, a2, …, an – неизвестные коэффициенты (коэффициенты регрессии).

228

Метод, позволяющей по выборке объемом N, которая содержит отдельные одновременно наблюдавшиеся значения переменных y и x1, x2, …, xn, оценить неизвестные значения коэффициентов регрессии a0, a1, a2, …, an, называется множественной регрессией. Уравнение регрессии (6.177) называет-

ся уравнением множественной регрессии.

Коэффициенты уравнения регрессии (6.177) так же, как и в случае парной регрессии, определяются по методу наименьших квадратов

Q y a0 a1 x1 an xn min . (6.178)

Последовательно дифференцируя это выражение по a0, a1, a2, …, an и приравнивая каждое из полученных уравнений нулю, можно получить систему нормальных уравнений

Для простоты вычислений используют следующий прием: все переменные стандартизируют, т.е. вместо переменных y и x1, x2, …, xn берут

где y, x1 , x2 , , xn - средние значения переменных y и x1, x2, …, xn

(по выборке объема N);

0 , 1 ,..., n - средние квадратические отклонения y и x1, x2, …, xn.

При использовании стандартизированных переменных существенно упрощается система нормальных уравнений, так как среднее значение признака в стандартизированном виде равно нулю, а дисперсия и среднее квадратическое отклонение – единице. Например, для признака t1 имеем:

Очевидно, что коэффициенты корреляции, вычисленные по формуле (6.181), равны коэффициентам корреляции, определенным в натуральном масштабе.

Уравнение множественной линейной регрессии в стандартизированном масштабе имеет вид

где t y - среднее значение стандартизированного результа-

тивного признака;

1, 2, …, n – стандартизированные коэффициенты

где rij – парный коэффициент корреляции между независимыми переменными хi и хj;

ri0 – парный коэффициент корреляции между зависимой переменной у i-й независимой переменной.

Если i = j , то парный коэффициент корреляции rii = 1. Решение системы уравнений (6.184) возможно как по

методу Крамера, так и матричным методом.

Если оценки коэффициентов регрессии обозначить теми же буквами, что и коэффициенты регрессии, то в натуральном масштабе их можно выразить следующим образом:

230

ai i y 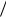i , i 1, n ;

a0 y a1 x1 a2 x2 an x n ,

где i – оценки коэффициентов регрессии в стандартизированном масштабе, полученные в результате решения системы (6.184).

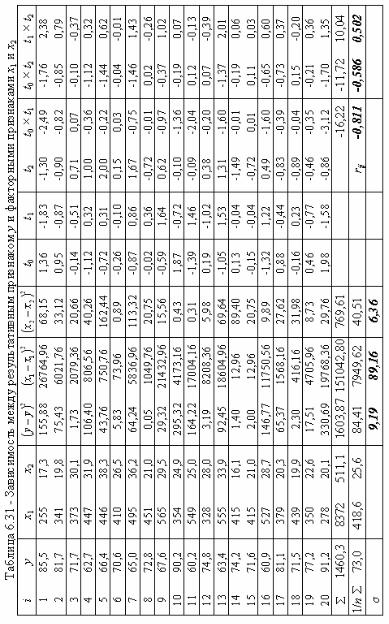
Продемонстрируем применение множественной регрессии на конкретном примере связи между результативным признаком у и двумя факторными признаками х1 и х2 (таблица 6.31). Связь между переменными предполагается линейной

ya0 a1 x1 a2 x2 .

Встроке таблицы, обозначенной символом суммы , приведены соответствующие суммы.