
- •Федеральное агенство по образованию
- •Введение
- •Общая задача оптимизации
- •1 Методические указания по решению злп в среде Exсel
- •1.1 Максимизация прибыли предприятия Постановка задачи
- •Решение
- •I этап: Составление математической модели
- •II этап: Решение задачи на эвм в среде ms Excel
- •III этап: Анализ решения задачи
- •1.2 Максимизация годового дохода Постановка задачи
- •Решение
- •I этап: Составление математической модели
- •II этап: Решение задачи на эвм в среде ms Excel
- •1.3 Специальные задачи линейного программирования
- •1.3.1 Задача целочисленного программирования
- •1.3.2 Транспортная задача Общая постановка транспортной задачи
- •Математическая модель транспортной задачи
- •1.3.2.1 Закрытая транспортная задача Минимизация стоимости перевозок кирпича
- •Решение
- •I этап: Составление математической модели
- •II этап: Решение задачи на эвм средствами пакета Excel
- •1.3.2.2 Открытая транспортная задача Постановка задачи
- •1.3.3 Задача о назначениях Постановка задачи
- •Решение
- •I этап: Составление математической модели
- •1.3.4 Двойственность в задачах линейного программирования. Анализ полученных оптимальных решений.
- •Задача оптимального использования ресурсов.
- •Решение.
- •I этап: Составление математической модели прямой злп
- •II этап: Решение задачи на эвм в среде ms Excel
- •Ш этап: Составление математической модели двойственной злп
- •Анализ влияния изменения правых частей ограничений на значения целевой функции (чувствительность решения к изменению запасов сырья).
- •2. Вопросы для самоконтроля:
- •3. Варианты заданий для контрольной работы по дисциплине
- •4. Требования к оформлению контрольной работы
1.3.3 Задача о назначениях Постановка задачи
Мастер должен расставить трех рабочих для выполнения трех операций. Причем, каждый рабочий должен выполнять только одну операцию и каждая операция должна выполняться только одним рабочим. Известно сколько минут в среднем тратит каждый из рабочих на выполнение каждой операции. Данные представлены в таблице:
|
Работники |
Работы | ||
|
1 |
2 |
3 | |
|
1 |
10 |
12 |
14 |
|
2 |
11 |
13 |
14 |
|
3 |
10 |
9 |
12 |
Как распределить рабочих по операциям, чтобы минимизировать суммарные затраты рабочего времени?
Решение
I этап: Составление математической модели
Элементы модели
Переменные (неизвестные) задачи
Так как в задании
требуется распределить рабочих по
операциям, то введем переменные
![]() ,
которые будут принимать только два
значении:
,
которые будут принимать только два
значении:
![]()
i=1,2,3, j = 1,2,3,.
В итоге мы имеем 9 неизвестных.
Целевая функция V
Цель задачи – минимизировать суммарные затраты рабочего времени. Т.к. время выполнения каждым рабочим каждой операции известно, то можно составить целевую функцию.
V будет иметь вид:
V=10*x11+12*x12+14*x13+
+11*x21+13*x22+14*x23+
+10*x31+9*x32+12*x33 (мин.)
Ограничения
Так каждый рабочий
должен выполнять только одну операцию
и каждая операция должна выполняться
только одним рабочим, то на неизвестные
![]() накладывается
ряд ограничений:
накладывается
ряд ограничений:
Каждый рабочий выполняет только одну операцию
x11+x12+x13=1, (22)
x21+x22+x23=1, (23)
x31+x32+x33=1, (24)
Каждая операция выполняется только одни рабочим
x11+x21+x31=1, (25)
x12+x22+x32=1, (26)
x13+x23+x33=1, (27)
xi –двоичные (28)
Примечание:
Ограничение 7 представляют собой следующие условие:
![]()
|
Неизвестные | |
|
i=1,2,3,j= 1,2,3,. | |
|
Целевая функция |
Ограничения |
|
V=10*x11+12*x12+14*x13+ +11*x21+13*x22+14*x23+ +10*x31+9*x32+12*x33 (мин.)
|
x11+x12+x13=1, x21+x22+x23=1, x31+x32+x33=1, x11+x21+x31=1, x12+x22+x32=1, x13+x23+x33=1, xi –двоичные
|
Численное решение задачи в Excel аналогично решению транспортной задачи.
1.3.4 Двойственность в задачах линейного программирования. Анализ полученных оптимальных решений.
Каждой задаче линейного программирования соответствует двойственная задача.
Первоначальная задача называется исходной или прямой.
Переменные двойственной задачи yi называются объективно обусловленными оценками, или двойственными оценками, или «ценами» ресурсов, или теневыми (скрытыми) ценами.
Двойственная задача по отношению к исходной задаче строится по следующим правилам:
1. Если исходная задача ставится на максимум, то двойственная ставится на минимум и наоборот.
2. Коэффициенты целевой функции исходной задачи становятся правыми частями ограничений двойственной задачи. Правые части ограничений исходной задачи становятся коэффициентами целевой функции двойственной задачи.
3. Если
![]() –матрица
коэффициентов исходной задачи, то
транспонированная матрица
–матрица
коэффициентов исходной задачи, то
транспонированная матрица![]() будет матрицей коэффициентов двойственной
задачи.
будет матрицей коэффициентов двойственной
задачи.
4. В задаче на
максимум все ограничения имеют знак
![]() (=), а в задаче на минимум все ограничения
имеют знак
(=), а в задаче на минимум все ограничения
имеют знак![]() .
.
5. Число переменных
в двойственной задаче равно числу
ограничений в исходной задаче. Каждому
ограничению исходной задачи соответствует
переменная двойственной задачи. Если
ограничение исходной задач имеет знак
(![]() ),
то соответствующая переменная двойственной
задачи неотрицательна. Если ограничение
имеет знак (=), то соответствующая
переменная двойственной задачи может
принимать положительные и отрицательные
значения и наоборот.
),
то соответствующая переменная двойственной
задачи неотрицательна. Если ограничение
имеет знак (=), то соответствующая
переменная двойственной задачи может
принимать положительные и отрицательные
значения и наоборот.
Модель исходной (прямой) задачи может быть записана следующим образом:
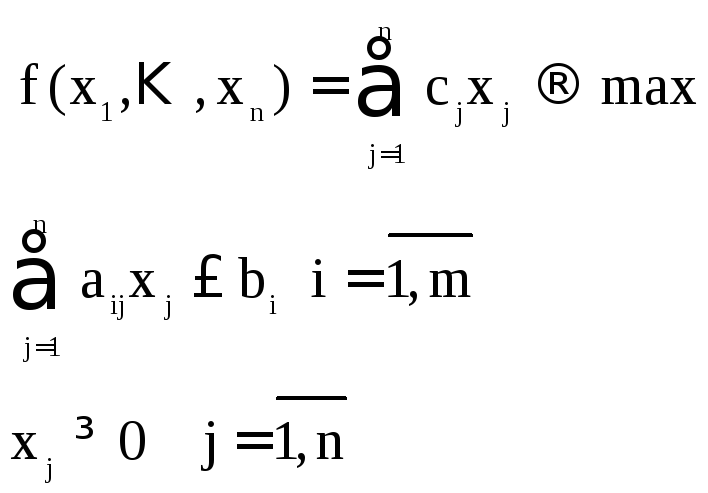
а модель двойственной задачи в этом случае –
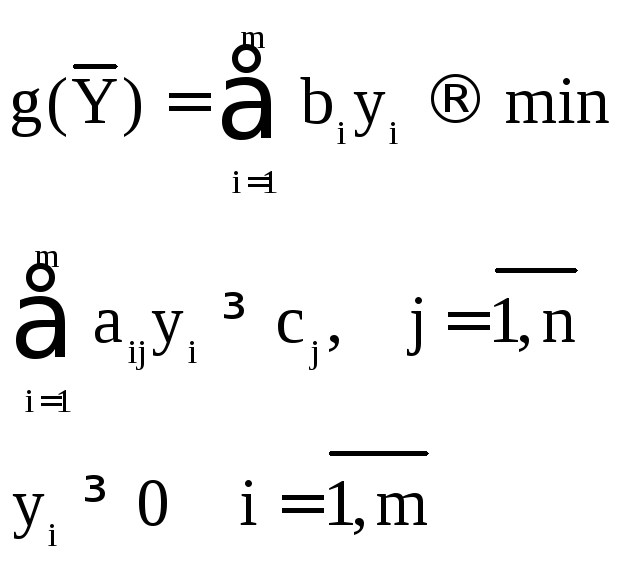
Теоремы двойственности:
Первая теорема двойственности. Для взаимно двойственных задач имеет место один из трех случаев:
1. Если существует
решение одной задачи, то существует
решение и второй задачи. Значения целевых
функций на оптимальных решениях обеих
задач равны
![]() .
.
2. Если решение одной задачи неограниченно, то другая задача несовместна.
3. Обе задачи несовместны.
Вторая теорема двойственности.
Пусть
![]() - допустимое решение прямой задачи, а
- допустимое решение прямой задачи, а![]() - допустимое решение двойственной
задачи. Чтобы данные решения были
оптимальными, необходимо и достаточно,
чтобы выполнялись следующие соотношения:
- допустимое решение двойственной
задачи. Чтобы данные решения были
оптимальными, необходимо и достаточно,
чтобы выполнялись следующие соотношения:
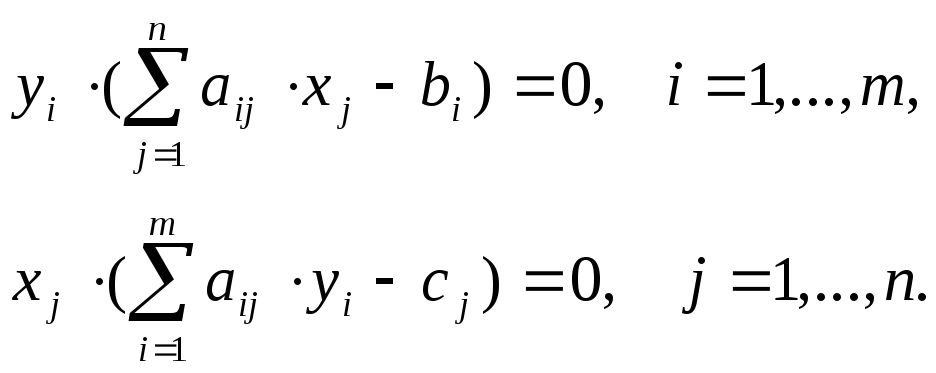 (29)
(29)
Имеет место и
обратное свойство: если допустимые
значения переменных
![]() удовлетворяют соотношениям (1), то они
являются оптимальными решениями обеих
задач.
удовлетворяют соотношениям (1), то они
являются оптимальными решениями обеих
задач.
Теорема об оценках (третья теорема двойственности).
Значения переменных
yi
в оптимальном решении двойственной
задачи представляют собой оценки влияния
свободных членов bi
системы ограничений – неравенств прямой
задачи на величину целевой функции
этой задачи:
![]()
Решая ЗЛП симплексным методом, мы одновременно решаем двойственную ЗЛП. Значения переменных двойственной задачи yi в оптимальном плане называют объективно обусловленными, или двойственными оценками. Они даются в строке оценок последней симплекс-таблицы по графам дополнительных переменных. Рассмотрим экономическую интерпретацию двойственной задачи на следующем примере.
