Методы Ньютона и простых итераций

ГЛАВА 1. РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

1. Метод Ньютона (метод касательных) 1

2. Метод простых итераций 3

1. Метод Ньютона (метод касательных)

Рассмотрим графическую иллюстрацию метода (рис. 1.4). Предположим, что графическим методом определено начальное приближение х₀ к корню. В точке x₀ вычислим левую часть решаемого уравнения f₀ = f(x₀), а также производную в этой точке f'(x₀). За следующее приближение к корню возьмем точку x₁, где касательная к функции f(x), проведенная из точки (x₀, f₀), пересекает ось абсцисс.

Уравнение прямой линии, проходящей через точку f₀ = f(x₀) и имеющей касательную f'(x₀), можно записать в виде:

у(х) = f(x₀)+f'(x₀)(x- x₀)

Чтобы найти x₁, необходимо решить уравнение y(x₁)=0:

у(х₁) = f'(x₀)(x₁- x₀)+ f(x₀)=0

Решая это уравнение, получим основную формулу метода Ньютона

Затем считаем точку х₁ в качестве началь­ной и продолжаем итерационный процесс. В общем виде для k+1-го шага итерационного процесса последнее соот­ношение принимает вид

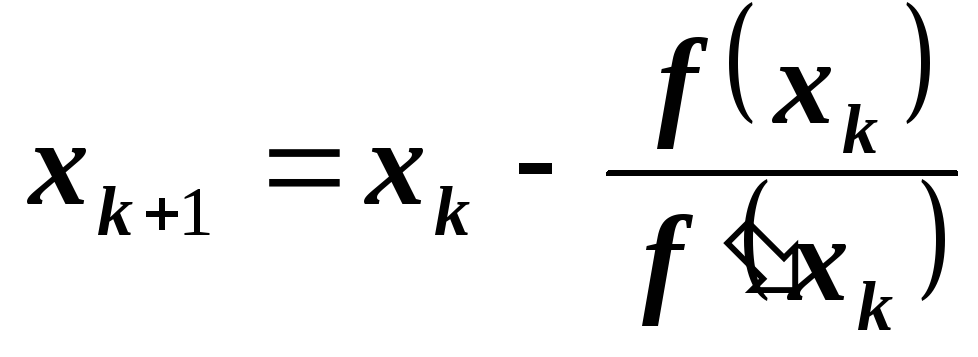(1.12)

Из рис. 1.4 видно, что таким способом можно приближаться к корню х*. При этом с каждой итерацией расстояние между очередным x_k+1 и предыдущим х_k приближениями к корню будет уменьшаться. Процесс уточнения корня закончим, когда выпол­нится условие

|x_k+1-x_k|< (1.13)

где  - допустимая погрешность определения корня.

Рис. 1.4. Метод Ньютона

Алгоритм Ньютона можно получить другим способом с помощью разложения в ряд Тейлора левой части уравнения f(x) вблизи корня x_k.

f(х) = f'(x_k)( x- x_k)+ f(x_k)+…

Пренебрегая вкладами второго и более высоких порядков и из условия, чтобы в результате следующей итерации функция была равна нулю:

f(x_k+1)=0

получим уравнение

f(x_k+1) = f'(x_k)( x_k+1- x_k)+ f(x_k)=0

Откуда получим решение в виде (1.13).

Метод Ньютона обладает высокой скоростью сходимости. Обычно относительная погрешность решения 10^-5 - 10^-6 достигается через 5-6 итераций.

Недостатком метода является необходимость вычисления на каждой итерации не только левой части уравнения, но и ее производной.

Можно, несколько уменьшив скорость сходимости, ограничиться вычислением производной f'(x) только на первой итерации, а затем вычислять лишь значения f(x), не изменяя производной f'(x). Это алгоритм так называемого модифицированного метода Ньютона (рис. 1.5).

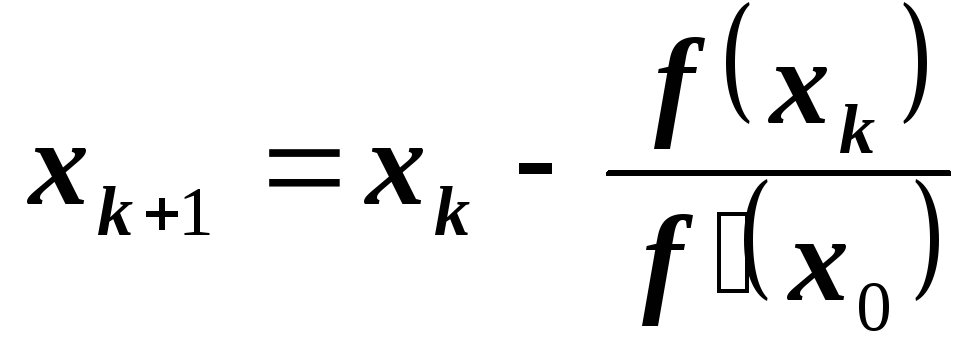(1.14)

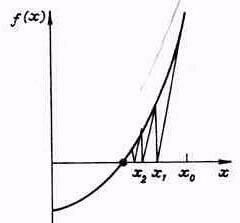
Рис. 1.5. Модифицированный ме­тод Ньютона

Метод Ньютона (1.13) - (1.14) можно использовать для уточнения корней в области комплексных значений х, что необходимо при решении многих прикладных задач, в частности при численном моделировании электромагнитных колебательных и волновых процессов с учетом временной и пространственной диссипации энергии. В этом случае начальное приближение корню х₀ необходимо выбирать комплексным.

2. Метод простых итераций

Исходное уравнение (1.1)

f(x)=0

всегда можно преобразовать к эквивалентному уравнению

х = (х) (1.24)

Пусть известно начальное приближение к корню x₀, тогда подставим его в правую часть уравнения (1.24) и получим новое приближение x₁ = (х₀), затем аналогичным образом получим x₂ = (х₁) и так далее. Таким образом, итерационное уравнение метода простых итераций имеет вид:

x_k+1 = (х_k) (1.25)

Необходимо установить, при каких условиях итерационный процесс (1.25) будет сходиться к корню уравнения х*.

Построим графики двух функций:

y₁(x)=x

y₂(x)=(x)

Координаты пересечения графиков этих функций и дадут корень исходного уравнения (1.24) х*.

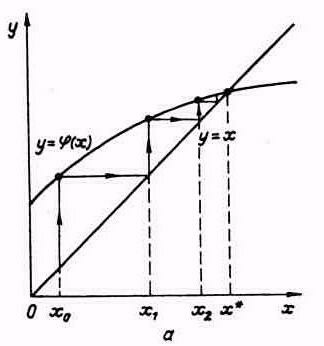
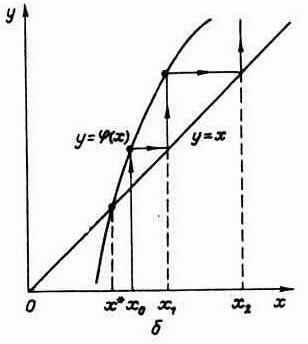
а) - односторонний сходящийся процесс	б) - односторонний расходящийся процесс
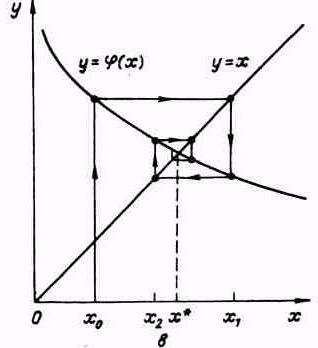
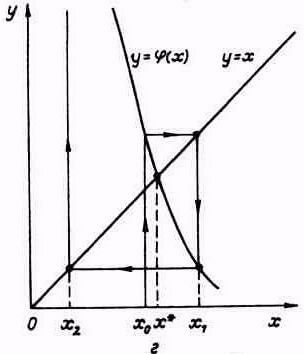
в) - двух­сторонний сходящийся процесс	г) - двухсторонний расходя­щийся процесс

Рис. 1.7. Метод простых итераций:

Рассмотрим процесс графически (рис. 1.7). Из графиков видно, что при ’(х)> 0 и при ’(х) < 0 возможны как сходящиеся, так и расходящиеся итерационные процессы. Скорость сходимости зависит от абсолютной величины производной ’(х). Чем меньше |’(х)| вблизи корня, тем быстрее сходится процесс.

Установим теперь критерий сходимости математически. Пусть х* - корень уравнения (1.26), т.е. имеем

х*=( х*)

Пусть _k и _k+1 - отклонения k и k+1 приближения корня от точного значения корня х*:

х_k=х*+_k

х_k+1=х*+_k+1

Если процесс уточнения осуществляется вблизи корня х*, то функцию (х) можно при­ближенно представить двумя членами ряда Тейлора:

( х_k)=( х*+_k)=( х*)+’( х*)_k

. Тогда итерационная формула (1.25) примет вид

Учитывая, что х* является корнем уравнения: х* = (х*), получим:

или

(1.26)

Для того чтобы итерационный процесс был сходящимся, должно выполняться условие

(1.27)

или

(1.28)

Из (1.26) видно, что максимальная сходимость будет в случае, если .

Переход от уравнения (1.1) к уравнению (1.24) можно осуществить различными способами в зависимости от вида функции f(x) . При таком переходе необходимо построить функцию такую (х), чтобы выполнялось условие сходимости (1.26). Рассмотрим один из общих алгоритмов перехода от уравнения (1.1) к уравнению (1.24). Умножим левую и правую части уравнения (1.1) на произвольную константу b и добавим к обеим частям неизвестное х. При этом корни исходного уравнения не изменятся

x+bf (х) = х +0b (1.27)

Введем обозначение

(х)=x+bf(x) (1.28)

и перейдем от соотношения (1.27) к уравнению (1.24).

Произвольный выбор константы b позволит обеспечить выполнение условия сходимости (1.26). Необходимо выбрать величину b такой, чтобы , тогда сходимость итерационного процесса будет двухсто­ронней (рис. 1.11, в). В этом случае в наиболее простом виде можно пред­ставить критерий окончания итерационного процесса

|x_k+1-x_k|< (1.29)

где  - заданная абсолютная погрешность вычисления корня.

Если функция (х) выбрана в виде (1.28), то производная по х от этой функции будет

’(х) = 1+bf’(х)

Т.е. условие (1.26) имеет вид:

или

Или

Поэтому константу b необходимо выбирать из интервала:

А) если f’(х)>0

-2/f’(х*)<b<0

Б) если f’(х)<0

0<b<-2/f’(х*)

Наибольшую скорость сходимости получим при ’(х*)=0, тогда

b = -1/f’(х*)

и итерационная формула (125) переходит в формулу Ньютона

x_k+1 =x_k - f(х_k)/f’(х_k)

Таким образом, метод Ньютона имеет самую высокую скорость сходимости из всех итерационных процессов.