6. Корреляционный анализ статистических данных

Понятие корреляции и регрессии появились в середине XIX века благодаря работам английских статистиков Ф. Гальтона и К. Пирсона. Первый термин произошел от латинского «corelatio» - соотношение, взаимосвязь. Второй термин от латинского «regression» - движение назад, введён Ф. Гальтоном. Статистические связи между переменными можно изучать методом корреляционного и регрессионного анализа. Основной задачей корреляционного анализа является выявление связей между случайными переменными и оценка её тесноты.

В статистических исследованиях для исследования зависимости между двумя видами данных (например, для анализа зависимости суммы выручки от числа обращений к продавцу; расхода сырья на единицу готовой продукции от степени чистоты сырья (стандарты на сырье); выхода реакции от температуры реакции; толщины плакировки от плотности тока; сопротивления удару от давления, при котором производилась обработка, и т. д.) применяется диаграмма разброса.[10]

Диаграмма разброса, так же как и метод расслоения, используется для выявления причинно-следственных связей показателей качества и влияющих факторов при анализе причинно-следственной диаграммы.

Диаграмма разброса строится как график зависимости между двумя параметрами. Если на этом графике провести линию медианы. То он позволяет легко определить имеется ли между этими двумя параметрами корреляционная зависимость. [5]

Построение диаграммы разброса выполняется в следующей последовательности.

1. Соберите парные данные (х, у), между которыми вы хотите исследовать зависимость, и расположите их в таблицу. Было бы хорошо иметь по меньшей мере 30 пар данных.

2. Найдите максимальные и минимальные значения для х и у . Выберите шкалы на горизонтальной и вертикальной осях так, чтобы обе длины рабочих частей осей х и у получились приблизительно одинаковыми (чтобы они уместились на экране компьютера или на стандартном листе бумаги), тогда диаграмму будет легче читать. При определении масштабов возьмите на каждой оси от 3 до 10 градационных делений и при обозначении этих делений используйте (для облегчения чтения) круглые числа. Если одна переменная — фактор, а вторая — характеристика качества, то выберите для фактора горизонтальную ось х, а для характеристики качества — вертикальную ось у.

3. На экране компьютера (на отдельном листе бумаги) начертите график и нанесите на него данные. Если в разных наблюдениях получаются одинаковые значения, покажите эти точки, либо рисуя концентрические кружки, либо нанося вторую точку рядом с первой.

4. Нанесите на диаграмму все необходимые обозначения, например:

а) название диаграммы;

б) интервал времени сбора данных;

в) число пар данных;

г) названия и единицы измерения для каждой оси;

д) дата составления диаграммы;

е) имя (и прочие данные) человека, который составлял эту диаграмму.

Убедитесь, что перечисленные выше данные, отраженные на диаграмме, понятны любому человеку, а не только тому, кто строил диаграмму.

Типичные виды диаграмм разброса (рассеивания) приведены на рис. 5.1.

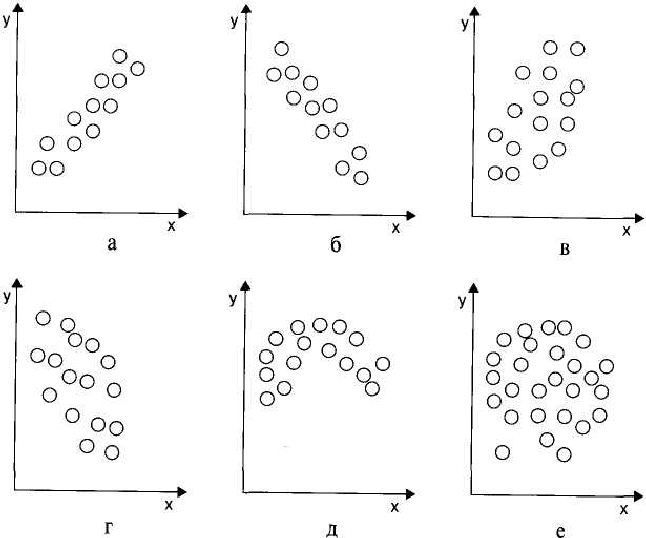
Рис. 6.1. Типичные виды диаграмм разброса (рассеивания):

а — сильная положительная корреляция;

б — сильная отрицательная корреляция;

в — слабая положительная корреляция;

г — слабая отрицательная корреляция;

д — криволинейная корреляция;

е — отсутствие корреляции.[14]

В случае прямолинейной корреляции на практике можно применять более простой метод оценки степени корреляционной связи – метод медиан, особенно удобный при исследовании технологического процесса с использованием данных, полученных на рабочем месте. Рассмотрим действие этого метода.

1. На диаграмме разброса проводятся вертикальная и горизонтальная линии медиан. Выше и ниже горизонтальной медианы, справа и слева от вертикальной медианы будет равное число точек. Если число точек окажется нечётным, следует провести линию через центральную точку.

2. В каждом из четырёх квадратов, получившихся в результате разделения диаграммы разброса вертикальной и горизонтальной медианами, подсчитывают число точек и обозначают их n₁, n₂, n₃, n₄ соответственно. Точки, через которые прошла медиана, не учитывают.

3. Отдельно складывают точки в положительных и точки в отрицательных квадратах по формулам: 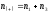(6.1)

(6.2)

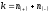(6.3)

4. Для определения наличия и степени корреляции по методу медианы используются специальная таблица (приложение Г) кодовых значений, соответствующих различным k при двух значениях коэффициента риска α (0.01 и 0.05). Если меньше из чисел 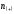или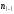оказывается равным или меньше табличного кодового значения, то корреляционная зависимость имеет место. При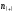>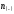существует прямая корреляция; при<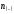- обратная.[6]

Для установления формы зависимости между переменными используют уравнения в виде:

y_x = b₀ + b₁x (6.4)

Коэффициент b₁ – выборочный коэффициент регрессии Y по X (будем обозначать символом b_yx). Этот коэффициент показывает, на сколько единиц в среднем изменяется переменная Y при увеличении переменной X на одну единицу.

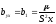, (6.5)

где 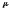- выборочная ковариация;

(6.6)

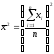
где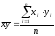(n – число пар), (6.7)

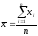, (6.8)

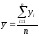(6.9)

S_x² – выборочная дисперсия переменной x:

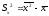(6.10)

где (6.11)

(6.12)

Тогда уравнение регрессии Y и X:

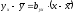(6.13)

а уравнение регрессии X и Y:

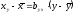(6.14)

где b_xy – выборочный коэффициент регрессии X по Y, показывающий на сколько единиц в среднем изменяется переменная X при увеличении переменной Y на одну единицу:

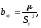(6.15)

S_y² – выборочная дисперсия переменной x:

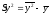(6.16)

где 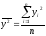(6.17)

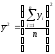(6.18)

Для оценки тесноты корреляционной зависимости используется

(6.19)

Т.е. коэффициент корреляции r переменных X и Y есть средняя геометрическая коэффициентов регрессии, имеющая их знак. В зависимости от того, насколько |r| приближается к 1, различают связь слабую, умеренную, заметную, достаточно тесную, тесную и весьма тесную. При r = 0 корреляционная связь отсутствует.[12]

В данной курсовой работе необходимо сделать корреляционный анализ статистических данных ТС-2010, № 400-450, математика и физика.

Таблица 6.1 – Исходные данные

Расчётная часть.

1) Рассмотрим ТС-2010, № 400-450, математика и физика.

Количество наблюдений n=51.

Min (X;Y)=(52;45)

Max (X;Y)=(71;70)

2) Построим диаграмму разброса.

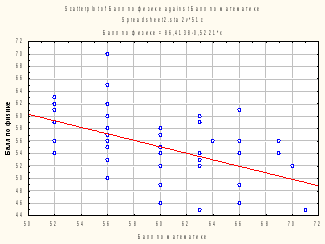
Рисунок 6.2 – Диаграмма разброса

Некоторые точки повторяются: (66;46) – 2 раза; (56;55) – 3 раза; (60;49) – 3 раза; (60;57) – 2 раза; (60;54) -2 раза; (56;56) – 3 раза; (52;63) – 2 раза; (52;62) – 2 раза; (63;54) – 2 раза.

3) Определим число точек:

n1=6 n₍₊₎ = n₁+n₃ = 6+3 = 9

n2=16 n_(-) = n₂+n₄ = 16+12 = 28

n3=3 n(-)>n(+)

n4=12 k = n₍₊₎+n_(-) = 37

При k=37 и коэффициенте риска α=0,01 кодовое число 10.

При k=37 и коэффициенте риска α=0,05 кодовое число 12.

n₍₊₎=9<10, n₍₊₎=9<12 => корреляционная зависимость имеет место.

Так как n(-)>n(+), корреляция обратная.

Таблица 6.2 – Статистика баллов учащихся за 2010 год (математика и физика)

Математика (X)	Физика (Y)	X*Y	X2	Y2
56	57	3192	3136	3249
52	63	3276	2704	3969
52	62	3224	2704	3844
52	61	3172	2704	3721
70	52	3640	4900	2704
69	56	3864	4761	3136
66	56	3696	4356	3136
66	49	3234	4356	2401
66	46	3036	4356	2116
66	46	3036	4356	2116
63	60	3780	3969	3600
63	53	3339	3969	2809
60	54	3240	3600	2916
56	56	3136	3136	3136
56	55	3080	3136	3025
56	55	3080	3136	3025
71	45	3195	5041	2025
66	61	4026	4356	3721
64	56	3584	4096	3136
63	59	3717	3969	3481
63	54	3402	3969	2916
63	52	3276	3969	2704
60	55	3300	3600	3025
60	54	3240	3600	2916
60	49	2940	3600	2401
60	49	2940	3600	2401
56	70	3920	3136	4900
56	62	3472	3136	3844
56	60	3360	3136	3600
56	58	3248	3136	3364
56	56	3136	3136	3136
56	55	3080	3136	3025
56	53	2968	3136	2809
52	63	3276	2704	3969
52	62	3224	2704	3844
52	59	3068	2704	3481
69	54	3726	4761	2916
63	54	3402	3969	2916
63	45	2835	3969	2025
60	58	3480	3600	3364
60	57	3420	3600	3249
60	57	3420	3600	3249
60	52	3120	3600	2704
60	49	2940	3600	2401
60	46	2760	3600	2116
56	65	3640	3136	4225
56	56	3136	3136	3136
56	50	2800	3136	2500
52	56	2912	2704	3136
52	54	2808	2704	2916
66	54	3564	4356	2916
Среднее значение 59,6078431	55,2941176	3281,569	3580,667	3085,686

₄₎

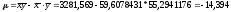
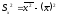=3580,667- 59,6078431² =27,572041.

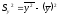=3085,686 – 55,2941176² =28,246559.

;

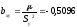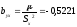
b₀₁ =87,7855; b₀₂ = 86,4138

Уравнения регрессии будут выглядеть следующим образом:

Y=86,4138-0,5221*x;

X=87,7855-0,5096*y.

5) Вычислим выборочный коэффициент корреляции:

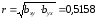
_{6) Построим диаграммы по каждому предмету отдельно.}

_{X- Математика}

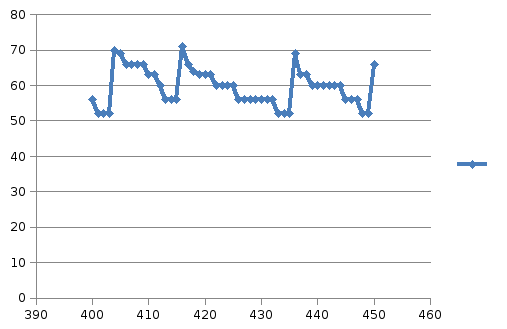
_{Рисунок 6.3 - Математика}

_{Y – Физика}

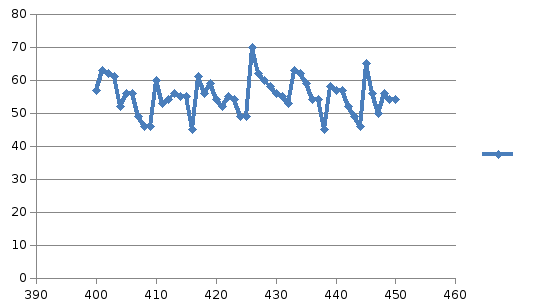
_{Рисунок 6.4 - Физика}

X	-	-	-	-	+	+	+	+	+	+	+	+	0	-	-	-	+	+	+	+	+	+	0
Y	+	+	+	+	-	+	+	-	-	-	+	-	-	+	0	0	-	+	+	+	-	-	0
X*Y	-	-	-	-	-	+	+	-	-	-	+	-	0	-	0	0	-	+	+	+	-	-	0

0	0	0	-	-	-	-	-	-	-	-	-	-	+	+	+	0	0	0	0	0	0	-	-	-	-	-	+
-	-	-	+	+	+	+	+	0	-	+	+	+	-	-	-	+	+	+	-	-	-	+	+	-	+	-	-
0	0	0	-	-	-	-	-	0	+	-	-	-	-	-	-	0	0	0	0	0	0	-	-	+	-	+	-

_{n'(+)=9; n'(-)=28; n'0=14;}

_{n(+)=n'(+)+n'0/2=9+7=16;}

_{n(-)=n'(-)+n'0/2=28+7=35;}

_k=16+35=51.

При k=51 и коэффициенте риска α=0,01 кодовое число 15.

При k=37 и коэффициенте риска α=0,05 кодовое число 18.

n₍₊₎=16>15 => корреляция отсутствует;

n₍₊₎=16<18 => корреляционная зависимость имеет место.

Так как n(-)>n(+) => корреляция обратная.