

При AC − B 2 = 0 требуется дополнительное исследование. Для некоторых функций экстремум существует, а для некоторых не существует.
Чтобы найти наибольшее и наименьшее значения функции в замкнутой области, надо:
1)найти стационарные точки и вычислить в них значения функции;
2)найти наибольшее и наименьшее значение функции на линиях, образующих границу области;
3)из всех найденных значений выбрать наибольшее и наименьшее значения.
4. Интегральное исчисление
(∫ f (x) dx)′ = f (x) , ∫ f ′(x) dx = f (x) +C
Дифференцирование и интегрирование – две взаимно обратные операции
|
|
|
|
|
|
|
|
∫(cf (x))dx = c∫ f (x)dx , |
|
∫(f + g)dx = ∫ fdx + ∫gdx , где c −const |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
- свойства неопределенного интеграла |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Таблица интегралов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
∫0 dx = C , |
|
|
|
|
∫dx = x +C , |
|
|
|
∫xn dx = |
|
|
|
xn+1 |
+C, n ≠ −1 , ∫ |
|
dx2 |
= − 1 |
+C , |
|
|
|
∫ |
dx |
|
= 2 |
|
+C |
, |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
∫ex dx = ex |
+C , |
|
∫a x dx = |
a x |
|
+C , |
|
|
|
|
|
|
|
∫dx = ln |
|
x |
|
|
+C , |
∫cos x dx =sin x + C , |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ln a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
∫sin x dx = −cos x + C , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
∫tg x dx = −ln |
|
cos x |
|
+C , |
∫ctg x dx = ln |
|
sin x |
|
|
+C , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
∫ |
|
dx |
|
|
= tgx + C , |
|
|
|
|
|
∫ |
|
dx |
|
|
|
= −ctgx + C , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
2 |
|
x |
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
∫ |
|
|
|
|
dx |
|
|
|
|
|
|
= arcsin |
x |
|
+C, a > 0 , |
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
= −arccos |
|
+C, a > 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
a |
2 |
− x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
2 |
− x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
∫ |
|
|
dx |
|
|
|
= |
|
|
arctg |
|
|
x |
|
+ C, a |
≠ 0 , |
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
dx |
|
= − |
|
arc сtg |
x |
|
|
+ C, а ≠ 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
2 |
|
2 |
|
|
|
|
|
a |
|
|
|
|
|
a |
2 |
2 |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
+ x |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ x |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
dx |
|
|
|
|
1 |
|
|
|
|
x −a |
|
|
+C, a ≠ 0 , |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+C , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ln |
x + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
∫ |
|
|
|
= |
|
ln |
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
x2 + a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x |
|
−a |
|
|
|
|
|
|
|
2a |
|
x +a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 + a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
∫sh x dx = ch x +C , |
|
|
|
|
∫ch x dx = sh x +C , |
|
|
∫th xdx = ln |
|
ch x |
|
+ C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
∫cth x dx = ln |
|
sh x |
|
+C , |
∫ |
dx |
|
|
|
= th x + C , |
|
|
|
|
|
|
∫ |
dx |
|
|
|
|
|
|
= −cth x + C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
x |
|
|
|
|
|
|
|
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ch |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sh |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
∫ |
|
|
|
dx = |
x |
|
|
|
|
|
+ a2 arcsin |
x |
+C |
, ∫ |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
x |
|
|
|
|
1 |
|
2n −3 |
∫ |
|
|
dx |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a2 − x2 |
|
a2 |
|
− x2 |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
(x |
2 2 |
) |
n |
|
|
2(n −1)a |
2 |
|
(x |
2 |
2 |
) |
n−1 |
2 |
2n − 2 |
(x |
2 |
2 |
) |
n−1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
+ a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ a |
|
|
|
|
|
|
a |
|
+ a |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
∫u dv = uv −∫v du |
- интегрирование по частям |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Если x =ϕ(t) , то |
|
∫ f (x)dx |
= ∫ f (ϕ(t))ϕ (t) dt |
- интегрирование заменой переменной |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
∫ f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
(ϕ(t))ϕ (t) dt = ∫ f (ϕ) dϕ - интегрирование методом подведения под знак |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
дифференциала. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫b |
|
f (x) dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
fср |
= |
a |
|
|
|
|
|
|
- среднее значение функции |
f (x) на отрезке [a;b] . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
b −a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Интегрирование правильных рациональных дробей |
|
P(x) |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Q(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
а) разложение знаменателя на множители
Q(x, y) =(x −a)m(x2 + p x +q)n ;
б) запись дроби в виде
7
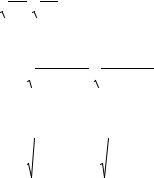
P(x) |
= |
A1 |
+ |
|
A2 |
|
+... + |
|
Am |
+ |
B1x + C1 |
+ |
|||
Q(x) |
(x − a)m |
(x − a)m−1 |
x − a |
(x2 + px + q)n |
|||||||||||
|
|
|
|
|
|
||||||||||
+ |
|
B2 x + C2 |
|
|
+... + |
|
Bn x + Cn |
|
. |
|
|
|
|||
(x2 + px + q)n−1 |
|
x2 + px + q |
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||
Интегрирование иррациональных выражений
а) Если корни в подынтегральном выражении имеют вид n xm , q
xm , q x p , то оно преобразуется в рациональную дробь подстановкой x = t k , где k - НОК показателей корней n, q .
x p , то оно преобразуется в рациональную дробь подстановкой x = t k , где k - НОК показателей корней n, q .
б) Если подынтегральное выражение содержит только корни n (ax +b)m , q
(ax +b)m , q (ax +b) p , то
(ax +b) p , то
оно преобразуется в рациональную дробь подстановкой ax +b = t k , где k - НОК показателей корней n, q .
в) Если подынтегральное выражение содержит только корни |
|
ax +b m |
|
ax +b p |
, то |
||
n |
|
, q |
|
||||
|
|
cx + d |
|
cx + d |
|
||
оно преобразуется в рациональную дробь подстановкой ax +b = t k , где |
k - НОК показателей |
|||||||||||||||||||
корней n, q . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cx + d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
г) Пусть подынтегральное выражение является дифференциальным биномом, т.е. имеет |
||||||||||||||||||||
вид xm (a +bxn ) p dx , где m, n, p - рациональные числа. |
|
|
|
|||||||||||||||||
г1) если p Z, то x = t s , s – НОК знаменателей дробей т и п, |
|
|
||||||||||||||||||
г2) |
если |
|
m +1 |
Z , то подстановка a +bxn = t s , |
s - знаменатель дроби р, |
|
||||||||||||||
|
n |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
г3) |
если |
m +1 |
|
+ p Z , то подстановка ax−n |
+b = t s , |
s - знаменатель дроби р. |
|
|||||||||||||
n |
|
|||||||||||||||||||
Интегрирование тригонометрических выражений: |
|
|
||||||||||||||||||
Неопределенные интегралы вида |
|
|
|
|
|
|||||||||||||||
∫sin ax sin bx dx, ∫sin ax |
cosbx dx, ∫cos ax |
cosbx dx |
|
|
|
|
|
|||||||||||||
с помощью тригонометрических формул |
|
|
|
|
|
|||||||||||||||
sinα sin β = cos(α − β) −cos(α + β) ; cosα cos β = cos(α − β) +cos(α + β) ; |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
sinα cos β = sin(α + β) +sin(α − β) |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
приводятся к интегралам |
|
|
|
|
|
|
||||||||||||||
∫sin kx dx = −cos kx |
+C, ∫cos kx dx = sin kx |
+C . |
|
|
|
|
|
|||||||||||||
|
|
k |
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
||
Неопределенные интегралы вида Im,n = ∫sinm x cosn x dx , где m и |
n - натуральные числа |
|||||||||||||||||||
находятся с помощью следующих замен: |
1−cos 2x |
,cos2 x = 1+ cos 2x |
,sin x cos x = sin 2x , |
|||||||||||||||||
а) если m и n |
- четные числа, то sin 2 x = |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
2 |
б) |
если хотя бы одно из чисел m и n |
- нечетное, то от нечетной степени отделяется |
||||||||||||||||||
множитель и вводится под дифференциал. Например |
|
|
|
|||||||||||||||||
Im,2k +1 = ∫sinm x cos2k +1 x dx = ∫sinm x cos2k x cos x dx = |
|
|
|
|
|
|||||||||||||||
= ∫sin m x (1−sin 2 x)k d(sin x) = (sin x = t)= ∫t m (1 −t 2 )k dt |
- сводится к интегралу от многочлена. |
|||||||||||||||||||
Интеграл вида ∫R(sin x,cos x) dx , где R(sin x,cos x) - рациональная функция от sin x и cos x с |
||||||||||||||||||||
помощью |
|
замены |
|
|
tg |
x |
=t |
приводится |
к |
интегралу |
от |
рациональной |
||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
функции: |
|
|
|
2t |
|
,1−t |
2 |
|
2dt |
. |
|
|
|
|
|
|
||||
∫R |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1+t |
2 |
2 |
2 |
|
|
|
|
|
|
|||||||||||
|
|
|
1+t |
|
|
1+t |
|
|
|
|
|
|
||||||||
8
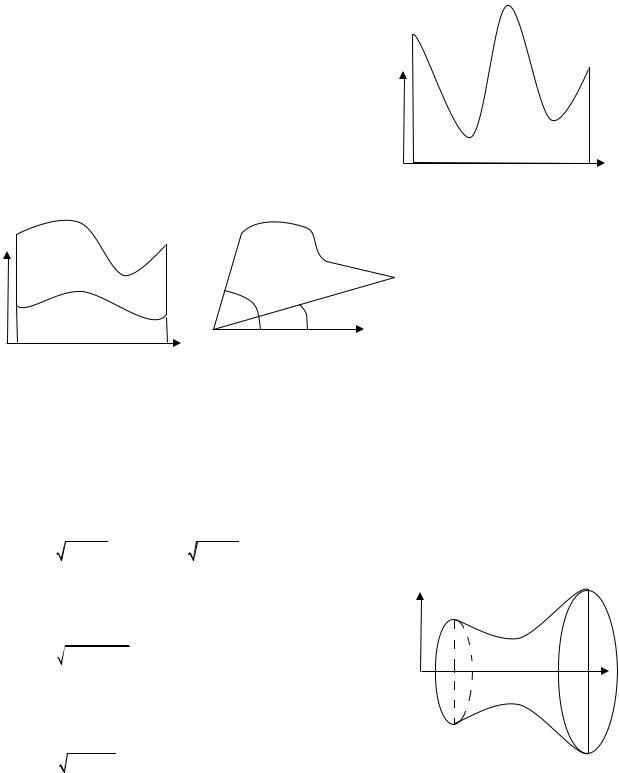
а) Вычисление площади фигуры
Площадь криволинейной трапеции, ограниченной сверху графиком функции y = f (x)
( f (x) ≥ 0 ), слева и справа соответственно прямыми x = a
и x = b , снизу – отрезком [a;b] |
оси ox (рис. 2) |
|
|||
вычисляется по формуле S = ∫b |
f (x) dx . |
|
|||
|
|
a |
|
|
|
|
Если y = f1 (x) |
и y = f2 (x) |
непрерывные функции |
|
|
на [a;b] и выполняется условие |
f2 (x) ≥ f1 (x) для любого |
|
|||
x [a;b] (рис. 3), то площадь фигуры, заключенной |
|
||||
между линиями вычисляется по формуле |
|
||||
у |
y = f2 (x) |
|
r = r (ϕ) |
||
|
|
|
|||
|
|
|
|
β |
|
|
y = f1 (x) |
х |
|
α |
ρ |
О a |
|
|
О |
|
|
Рис. 3 |
b |
|
Рис. 4 |
|
|
|
|
|
|
|
|
формуле
S= 1 ∫β r2 (ϕ) dϕ .
2 α
y = f (x)
у
|
|
х |
О a |
Рис. 2 |
b |
|
|
S = ∫b ( f2 (x) − f1 (x))dx .
a
Площадь криволинейного сектора (рис. 4), ограниченного линией, заданной в полярных координатах уравнением
r = r(ϕ) и двумя лучами ϕ =α и ϕ = β , α < β , вычисляется по
б) Вычисление длины кривой
Если линия задана на плоскости уравнением y = f (x) или x =ϕ(y) , то длина l дуги линии между точками A(a; c), B(b, d) вычисляется по формуле
b |
|
|
d |
|
|
||
l = ∫ |
1+(y ) |
|
dx |
или l = ∫ |
1+(x ) |
|
dy . |
|
′ |
2 |
|
|
′ |
2 |
|
a |
|
|
c |
|
|
||
Если линия задания параметрическими уравнениями |
|||||||
x = x(t), y = y(t) , |
то длина l дуги линии между |
||||||
точками M1 (t1 ), M 2 (t2 ) |
вычисляется по формуле |
||||||
t2
l = ∫
 (x′)2 +(y′)2 dt .
(x′)2 +(y′)2 dt .
t1
Если линия задания уравнением r = r(ϕ) в полярных
координатах, то длина l дуги линии между точками M1 (ϕ1 ), M 2 (ϕ2 ) вычисляется по формуле
у
y = f (x)
Оa 
ϕ2 |
|
|
|
|
dϕ . |
l = ∫ |
r |
2 |
′ |
2 |
|
|
+(r ) |
|
|||
ϕ1 |
|
|
|
|
|
в) Вычисление объема |
|||||
Объем тела вращения, полученного при повороте криволинейной трапеции (ограниченной графиком функции y = f (x) , прямыми x = a, x = b и осью ox ) вокруг оси
b х
ox (рис.
5), равен V =π∫b |
f 2 (x) dx . |
a |
|
9

|
|
|
г) Площадь поверхности вращения, полученной при вращении криволинейной линии, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
заданной уравнением y = f (x) |
|
на отрезке [a;b] , вокруг оси ox , равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
P = 2π∫b |
f (x) |
|
|
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1+ f ′2 (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = f (x) |
|
|
|
|
|
|
|
|
|
|
r = r(ϕ) |
|
|
|
|
|
|
|
|
|
x = x(t), y = y(t) |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
1 |
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
S -площадь фигуры |
|
|
|
|
|
|
|
∫ f (x)dx |
|
|
|
|
∫r 2 (ϕ)dϕ |
|
|
|
|
|
|
|
|
∫2 |
y(t)x′(t) dt |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
2 |
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l - длина линии |
|
|
|
|
∫ |
|
|
|
|
′ |
2 |
dx |
|
|
|
|
|
∫ |
|
r |
2 |
+(r′) |
2 |
dϕ |
|
|
|
∫ |
|
(x′) |
2 |
+ |
(y′) |
2 |
dt |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
1+( f ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
V -объем тела вращения |
|
|
|
π∫ f 2 (x)dx |
|
|
|
|
|
∫r |
3 sin ϕdϕ |
|
|
|
|
|
|
|
π ∫2 y 2 (t)x′(t) dt |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
P - площадь поверхности |
|
2π |
∫ f (x) 1+( f ′)2 (x)dx |
|
2π∫r sinϕ r 2 +(rϕ′)2 dϕ |
|
|
|
2πy∫y(t) (x′)2 +(y′)2 dt |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
вращения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Для четной функции f (x) |
на отрезке [−a; a] выполняется равенство ∫a |
f (x) dx = 2∫a |
f (x) dx . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−a |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||
Для нечетной функции f (x) на отрезке [−a; a] выполняется равенство |
∫a |
f (x) dx = 0 . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если функция |
f (x) |
|
имеет период T и на отрезке [0;T ] |
существует первообразная для |
f (x) , то |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
для любого a |
справедливо равенство a∫+T |
|
f (x) dx = T∫ f (x) dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
V. Решение некоторых примеров |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
I. Методы вычисления пределов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
1. Вычисление пределов на основе определения и свойств предела |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
Пример 1. Доказать, что |
|
lim (3x +5) = 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Решение. а) Пусть ε |
|
|
|
- |
произвольное |
|
положительное |
|
число. |
|
Составим |
|
неравенство |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
(3x +5) −2 |
|
< ε |
|
3x +3 |
|
< 3 |
|
x +1 |
|
< |
ε . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
x +1 |
|
< ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
число δ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
Рассмотрим |
|
. Если выполняется неравенство |
|
|
, |
|
из |
него |
получаем |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(3x +5) −2 |
|
< ε . |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
ε |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Таким |
образом |
доказано, что |
|
любого положительного |
числа |
|
нашлось |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
положительное число δ = ε |
, такое, |
что если переменная |
x удовлетворяет неравенству |
|
x +1 |
|
< δ , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3x +5) −2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
то функция |
f (x) = 3x +5 |
|
|
удовлетворяет |
неравенству |
|
|
|
|
< ε , |
поэтому |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
lim (3x +5) = 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x→−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x −7 ; б) |
|
|
|
|
|
2x−5 |
|
|
|
lim sin 2x |
|
|
|
|
|
|
|
|
|
|
|
|
1 . |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
Пример 2. Найти а) lim |
|
lime |
x−4 |
|
; в) |
; г)lim xcos |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x→5 |
|
x −3 |
x→3 |
|
|
|
|
|
x→∞ |
|
x |
|
|
|
|
|
x→0 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
10

а) Существует lim(2x −7) = 3, существует |
||||
x→5 |
|
|
lim f (x) |
|
|
f (x) |
|
||
от нуля. Применяя равенство lim |
= |
x→x0 |
||
g(x) |
lim g(x) |
|||
x→x0 |
|
|||
|
|
|
x→x0 |
|
lim(x −3) = 2 , причем этот предел отличен |
|||
x→5 |
|
|
|
, получаем lim |
2x −7 |
= |
3 . |
x→5 |
x −3 |
|
2 |
|
|
2x−5 |
|
y = eu , |
|
|
2x −5 |
|
||
б) |
Функцию y = e |
x−4 |
представим в виде сложной функции |
где |
u = |
. |
||||
|
||||||||||
|
|
|
|
|
|
|
|
x −4 |
||
Функция |
y = eu непрерывна на всей числовой оси, |
функция u = 2x −5 непрерывна в точке |
||||||||
|
|
|
|
x −4 |
|
|
|
|
||
x = 3. Будем использовать равенство lim f [ϕ(x)] = f [ lim ϕ(x)], |
которое |
для |
непрерывной |
|||||||
|
|
|
x→x0 |
x→x0 |
|
|
|
|
|
|
функции y = f (u) означает, что под знаком непрерывной функции можно переходить к пределу:
|
2x−5 |
lim |
2x−5 |
|
1 . |
|
lime x−4 |
x−4 = e−1 = |
|||||
= ex→3 |
||||||
x→3 |
|
|
|
e |
||
в) При x → ∞ числитель дроби является ограниченной функцией sin 2x ≤1, а знаменатель является бесконечно большой функцией, поэтому их отношение является бесконечно малой функцией
при x → ∞, следовательно lim sin 2x |
= 0 . |
|
|
|
|
|
|
|
|||
x→∞ |
x |
|
|
|
|
|
|
|
|
1 |
|
г) Произведение бесконечно малой величины x при x → 0 на ограниченную величину cos |
|||||||||||
|
|
|
|
|
|
|
1 = 0 . |
|
|
x |
|
является бесконечно малой величиной, поэтому lim xcos |
|
|
|
||||||||
|
|
|
|
|
x→0 |
x |
|
|
|
||
2. Выделение выражений, стремящихся к нулю, в качестве множителей |
|
||||||||||
Пример 3. Найти а) lim |
|
x3 −8 |
|
; б) |
lim |
2x3 +9x2 +14x +8 |
. |
|
|
|
|
|
|
|
|
|
|
|
|||||
x→2 x2 −5x +6 |
|
x→−2 |
x + 2 |
|
|
|
|||||
а) Предел вычисляется при x → 2, но x ≠ 2 . |
При x → 2 числитель стремится к 0 |
и |
|||||||||
знаменатель также стремится к нулю. Получаем неопределенность вида |
|
0 |
|
||||||||
|
. Пытаемся выделить в |
||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
числителе и в знаменателе множитель (x −2), чтобы потом упростить дробь. |
|
|
|
|||||||
lim |
x3 |
−8 |
= lim |
(x −2)(x2 + 2x + 4) |
= lim |
(x2 |
+ 2x + 4) |
= |
12 |
= −12 . |
|
5x +6 |
(x −2)(x −3) |
|
(x −3) |
−1 |
|||||
x→2 x2 − |
x→2 |
x→2 |
|
|
|
|||||
б) Первый способ. Чтобы выделить в числителе
множитель x + 2, разделим числитель на этот одночлен “столбиком”.
lim |
2x3 |
+ 9x2 +14x + 8 |
= |
|
|
|
x + 2 |
||
x→−2 |
|
|
. |
|
= lim (2x2 |
+ 5x + 4) = 2 |
|
||
x→−2 |
|
|
|
|
- 2x3 +9x2 +14x +8 x + 2 |
||||||
2x3 + 4x2 |
|
|
2x2 |
+5x + 4 |
||
- |
5x |
2 |
+ |
14x |
||
|
|
|
||||
|
5x2 +10x |
|
|
|||
|
|
|
- |
4x +8 |
|
|
|
|
|
|
4x +8 |
|
|
Второй способ. Представим числитель дроби в |
0 |
виде произведения одночлена x + 2 на многочлен |
|
второй степени ax2 +bx +c , т.е.
11

2x3 +9x2 +14x +8 = (x + 2)(ax2 +bx +c) ,
2x3 +9x2 +14x +8 = ax3 +(2a +b)x2 +(c + 2b)x + 2c . Два многочлена равны при
любом значении переменной x , тогда и только тогда, когда равны коэффициенты при соответствующих степенях:
Сравнивая коэффициенты при x3 , получим 2 = a или a = 2 .
Сравнивая коэффициенты при x2 , получим 9 = 2a +b или b = 5. Сравнивая коэффициенты при x , получим 14 = c + 2b или c = 4.
Сравнивая коэффициенты при x0 , т.е. сравнивая константы, получим 8 = 2c или c = 4. Следовательно 2x3 +9x2 +14x +8 = (x + 2)(2x2 +5x + 4) . Далее вычисление предела
проводится аналогично первому способу.
Запомните этот метод разложения многочлена на множители как метод неопределенных коэффициентов.
Третий способ. Введем обозначение x + 2 = t , тогда x = t −2.
2x3 +9x2 +14x +8 = 2(t −2)3 +9(t −2)2 +14(t −2) +8 = 2t3 −3t2 + 2t = t(2t2 −3t + 2)
lim |
2x3 +9x2 +14x +8 |
= lim |
t (2t2 −3t + 2) |
= lim(2t2 −3t |
+ 2) = 2 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x→−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t→ |
0 |
|
|
|
|
|
|
|
|
|
3 |
|
|
t→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
+ |
1 |
7 − x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
Пример 4. а) lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; б) lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x2 −9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→1 |
|
x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
Решение. а) Для упрощения в числителе неопределенности вида (∞ −∞) умножим числитель |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
и знаменатель на сопряженное число |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
= lim |
( |
|
|
|
|
|
|
− |
|
|
|
|
|
)( |
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
)= |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
lim |
|
|
|
|
|
x +1 |
7 − x |
|
|
x +1 |
|
7 |
− x |
|
|
|
|
x +1 |
|
|
7 − x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
x→3 |
|
|
|
|
|
x2 − 9 |
|
|
|
|
|
|
|
|
|
|
x→3 |
|
|
|
|
|
(x2 − 9)( |
|
|
|
x +1 + 7 − x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2(x − 3) |
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
1 |
. |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x→3 (x − 3)(x + 3)( |
|
|
|
x +1 + 7 − x ) |
|
|
|
x |
→3 |
(x +3)( x +1 + 7 |
− x ) |
|
|
12 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
б) Первый способ. Используя формулы сокращенного умножения, умножим числитель и |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
знаменатель дроби на такие выражения, |
|
чтобы выделить выражение (x −1) , |
стремящееся к нулю и |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
затем сократить на него |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 +3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
3 |
|
|
|
|
−1 |
|
|
|
|
|
|
|
(3 |
|
|
|
|
−1)(3 |
|
|
|
+1)( |
|
|
|
+1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
(x −1) ( |
|
+1) |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
x |
x |
x |
x |
= lim |
|
|
|
x |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
lim |
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
x→1 |
|
|
|
x→1 ( |
x |
−1)( |
x |
+1) (3 |
x |
+3 |
x |
+1) |
|
|
|
|
|
x |
→1 (x −1) (3 |
x |
+3 |
x |
+1) |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
( |
|
|
|
|
+1) |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
= lim |
|
|
|
x |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 +3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
x→1 (3 |
|
|
+1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
Второй способ. Рассмотрим замену 6 |
|
= t , тогда 3 |
|
|
|
= t2 , |
|
|
= t3 . При x →1 получаем |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
|
|
x |
|
x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
t →1. После замены переменной получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|
|
−1 |
|
|
|
|
|
|
|
|
t2 −1 |
|
|
|
|
|
|
|
|
|
|
|
(t −1)(t +1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t +1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
lim |
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
= |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 −1 |
|
(t −1)(t2 |
+t +1) |
|
2 +t |
+1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x→1 |
|
x −1 |
|
|
t→1 t |
|
|
|
t→1 |
|
|
|
|
|
|
x→1 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Замечание. |
Для |
|
|
|
|
|
показателей |
|
корней |
|
n, m |
|
|
|
выбираем |
наибольшее общее |
|
|
кратное |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
k= НОК(n, m) и обозначаем k x = t .
x = t .
3.Использование бесконечно малых величин
12
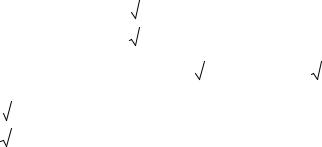
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
−1 |
|
|
|
|
arctg 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Пример 5. Найти а) lim |
|
|
|
|
|
|
|
|
|
|
|
|
; б) |
lim |
|
sin 3x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
→0 |
|
x +1 |
−1 |
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Решение. а) При x → 0 получаем 3 |
|
~1 |
+ 1 x , |
|
|
|
|
|
~1+ 1 x , поэтому |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
1+ x |
|
|
1+ x |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
− |
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
lim |
|
x +1 |
= |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
x +1 − |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
б) При x → 0 имеем 2x → 0 , 3x → 0 , поэтому arctg 2x ~ 2x , sin3x ~ 3x |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
lim arctg 2x |
= lim |
|
2x = 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
x→0 |
|
|
sin3x |
|
|
|
x→0 |
|
3x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
4. Использование формулы Тейлора для вычисления пределов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
Пример 6. Найти lim |
sin x − x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Используя разложение функции y = sin x в ряд Тейлора, получим |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
sin x − x |
|
|
|
|
|
|
|
x − |
x3 |
|
+ |
|
x5 |
− R |
(x) − x |
|
|
|
− |
x3 |
+ |
|
x5 |
|
− R (x) |
|
1 |
|
|
1 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
3! |
|
5! |
|
|
|
3! |
5! |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
lim |
= lim |
|
|
|
|
|
|
|
7 |
|
|
|
|
= lim |
|
|
|
|
7 |
|
|
= − |
|
= − |
. |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
3! |
6 |
||||||||||||||||||||||
x→0 |
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
→0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
5. Использование поведения величин при стремлении аргумента к бесконечности |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
Пример 7. а) lim |
|
2x2 + x −3 |
; б) lim |
2x+1 +5x+1 |
|
; в) |
lim |
2x+1 +5x+1 |
; г) lim xsin |
1 |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2x |
+5x |
|
|
2x |
+5x |
x |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x→∞ 5x4 −2x +1 |
|
|
|
|
x→+∞ |
|
|
|
|
x→−∞ |
|
|
|
x→∞ |
|
|
||||||||||||||||||||||||||||||||
а) Имеем неопределенность |
|
∞ |
|
|
|
x → ∞ поведение числителя |
и знаменателя |
|||||||||||||||||||||||||||||||||||||||||||||||
|
∞ |
. При |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
определяется членами с наибольшими показателями степеней (соответственно 2x2 и 5x4 ). Разделим
числитель и |
|
знаменатель |
на |
x4 , |
т.е. |
на |
|
x |
|
с |
|
наибольшим показателем степени числителя и |
||||||||||||||
знаменателя. |
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
3 |
|
|
|
|
|
|
|
|||
|
|
2x2 + x −3 |
|
∞ |
|
|
|
+ |
|
|
− |
|
|
|
0 |
+ 0 |
+ 0 |
|
||||||||
|
|
|
2 |
|
3 |
|
4 |
|
|
|
|
|||||||||||||||
lim |
|
|
|
= |
= lim |
|
x |
|
|
|
|
x |
|
|
|
x |
|
= |
5 |
− 0 |
− 0 |
= 0. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
x→∞ 5x4 − 2x +1 |
|
∞ |
x→∞ |
5 |
|
|
|
2 |
|
1 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
− |
|
|
+ |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
x3 |
x4 |
|
|
∞ |
|
|
|
||||||||||||
б) При |
x → +∞ |
имеем неопределенность вида |
|
. Поведение числителя и знаменателя |
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
определяется вторыми слагаемыми, которые возрастают быстрее первых слагаемых. Разделив числитель и знаменатель на 5x , получим
|
|
|
|
|
|
|
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
2x+1 +5x+1 |
|
∞ |
|
|
2 |
5 |
|
+5 |
|
0 +5 |
|
|
2 |
|
|
2 x |
|||
lim |
|
= |
|
= |
lim |
|
|
|
= |
|
= 5 |
, т.к. |
|
<1 |
и lim |
|
|
= 0 . |
||
2x +5x |
|
2 |
x |
|
0 +1 |
5 |
5 |
|||||||||||||
x→+∞ |
|
∞ |
|
x→+∞ |
+1 |
|
|
|
|
x→+∞ |
|
|
||||||||
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
13
в) При x → −∞ |
|
0 |
|
имеем неопределенность вида |
0 |
. Поведение числителя и знаменателя |
|
|
|
|
определяется первыми слагаемыми, которые убывают медленнее вторых слагаемых. Разделив числитель и знаменатель на 2x , получим
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||||
|
|
|
|
|
|
2x+1 |
|
+ 5x+1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
2 + 5 |
2 |
|
|
|
|
|
|
|
2 + 0 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|||||||||||||||||||||||||||
|
lim |
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2, т.к. |
|
>1 и |
lim |
|
= 0. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
2x |
|
+ 5x |
|
|
0 |
|
|
|
|
|
|
|
5 |
x |
|
|
1 + 0 |
|
|
2 |
2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x→−∞ |
|
|
|
|
|
|
|
|
x→−∞ |
1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→−∞ |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
г) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
0 |
|
|
обозначим |
|
= t. |
|
|
|
|
|
|
|
|
|
sin t |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
lim xsin |
= (∞ 0) = lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
=1. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
x |
|
|
|
1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
||||||||||||||||||||||||||||||||||||||||||
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
Если x → ∞, тоt |
|
|
|
|
|
|
|
t→0 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
6. Использование замечательных пределов |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin5x |
|
|
|
|
|
|
|
|
|
|
3x − 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
Пример 8. Найти а) lim |
|
|
|
|
|
|
|
|
|
; б) |
|
lim |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
x2 |
|
|
|
|
3x + 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
а) |
|
Если |
x → 0, |
то |
|
|
5x → 0 . |
Выделим |
в |
|
|
|
знаменателе |
дроби |
выражение |
|
5x , |
чтобы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
использовать затем первый замечательный предел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
lim |
sin5x |
= lim |
sin5x |
|
5 |
|
=1 lim |
5 |
= |
∞. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
x2 |
|
|
|
5x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
x→0 |
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
x→0 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
б) Используем второй замечательный предел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
3x − |
2 x |
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
(3x |
+4) −6 x |
|
|
|
|
|
|
|
|
|
|
3x +4 |
|
|
|
|
|
6 |
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
lim |
3x + |
|
|
|
|
|
= |
(1 |
|
)= lim |
|
|
3x +4 |
|
|
|
|
|
|
= lim |
3x +4 |
− |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x→∞ |
4 |
|
|
|
|
|
|
|
|
|
|
|
x |
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
3x +4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x+4 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
− |
|
|
|
|
|
− |
|
|
|
x |
|
lim |
−6x |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
3x+4 |
|
|
|
|
|
|
|
|
−2 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
= lim |
1+ |
|
− |
|
|
|
|
|
|
|
|
|
= lim 1 |
+ |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ex→∞ |
3x+4 |
|
= e |
|
|
. |
||||||||||||||||||||||||||||||
|
|
3x + 4 |
|
3x + 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
x→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
7. Использование правила Лопиталя |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
Пример 9. а) lim |
shx |
, б) |
lim |
|
x2 |
|
, в) |
lim |
xln x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
x |
|
|
3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x |
→0 |
|
|
|
|
|
|
x→+∞ |
|
|
|
x→0+0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
shx |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
chx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Решение а) lim |
= |
|
= lim |
|
(shx) |
= lim |
|
= |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
x2 |
|
∞ |
|
|
|
lim |
(x2 )′ |
|
|
|
2 |
|
|
|
lim |
|
|
|
x |
|
|
∞ |
|
|
|
|
|
2 |
|
|
lim |
|
|
(x)′ |
|
|
|
|
|
|
2 |
|
|
lim |
1 |
= 0. |
|
|||||||||||||||||||||||||||||||
|
|
= |
|
= |
|
|
(3x )′ |
= |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
== |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
ln3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
x→+∞ 3x |
|
∞ |
|
|
x→+∞ |
|
|
|
|
ln3 x→+∞ 3x |
|
|
|
|
|
|
|
x→+∞ (3x )′ |
|
|
|
|
ln2 3 x→+∞ 3x |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln x |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
в) |
|
lim |
xln x =(0 ∞)= |
lim |
= |
|
lim |
|
|
|
|
|
|
x |
|
|
|
= |
|
lim (−x) = 0 . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
x→0+0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x→0+0 |
|
|
x→0+0 − |
|
|
1 |
|
|
|
|
x→0+0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
14
