
ODD
.pdf
Рис.2.6
21
Задание № 3 (К1)
ОПРЕДЕЛЕНИЕ КИНЕМАТИЧЕСКИХ ХАРАКТЕРИСТИК ДВИЖЕНИЯ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ
ЕЕ ДВИЖЕНИЯ
Цель задания: Научиться определять уравнение траектории, скорость и ускорение точки при координатном способе задания движения, а также ее
нормальное и касательное ускорения и радиус кривизны траектории в момент времени t = t1.
Для выполнения задания необходимо изучить раздел кинематика точки по рекомендованной литературе:
[1]§§ 36-46;
[2]§§ 65,66,71,73,74,76;
[5]глава III §§ 1,2.
Вопросник-минимум для защиты задания № 3 (К1):
1)Какие кинематические способы задания движения существуют? В чем состоит векторный способ?
2)В чем заключаются координатный и естественный способ задания движения точки?
3)Как по уравнениям движения точки в координатной форме определить ее траекторию (привести примеры)?
4)Что называют скоростью и ускорением точки?
5)Как определяются проекции скорости и ускорения точки на неподвижные оси декартовых координат?
6)Что называется кривизной и радиусом кривизны траектории в данной точке?
7)Ввести понятие естественных осей координат и определить проекции скорости на эти оси.
8)Определить проекции ускорения точки на естественные оси координат.
Написать формулы для вычисления касательного и нормального ускорений. В какой плоскости лежит ускорение точки (ввести понятие соприкасающейся плоскости)?
9)Как направлены вектора скорости и касательной составляющей ускорения при ускоренном и замедленном движении точки?
10)Дайте определения равномерного и равнопеременного движения точки и напишите уравнения этих движений.
Постановка задачи: Точка М движется в плоскости Oxy .
22
Уравнения движения точки заданы в виде: x = x(t), y = y(t).
Зависимость x = x(t) указана непосредственно на рисунках (3.2) и (3.3), а зависимость y = y(t) имеет общий вид:
y = α1 sin πt + α2 cosπt + α3 sin2 πt + α4 cos2 πt + α5 cos 2πt + α6 ,
где значения коэффициентов αi даны в таблице 3.1.
Координаты точки x и y выражены в сантиметрах, а время t в
секундах.
Требуется по заданным уравнениям движения точки установить вид её траектории и для момента времени t = t1 найти положение точки на
траектории; ее скорость; полное, касательное и нормальное ускорение, а также радиус кривизны траектории в соответствующей точке.
Изобразить на рисунке траекторию точки, ее положение, скорость и ускорение в данный момент времени t = t1.
ПОРЯДОК РАСЧЕТА И ПРИМЕР НА ВЫПОЛНЕНИЕ ЗАДАНИЯ № 3 (К1).
Пусть уравнения движения точки М имеют вид: |
|
|
|
|
x = 0,7cos 2πt + 0,9 , |
y = 1,3cosπt + 0,8, |
|
|
(26) |
где x , y измеряются в см, t - в сек. |
|
|
|
|
Найти уравнение траектории и для момента времени t = t |
= |
7 |
с. |
|
|
1 |
|
3 |
|
определить: положение точки на траектории; скорость и ускорение точки; ее касательное и нормальное ускорения; радиус кривизны той точки траектории, где в данный момент времени находится движущаяся точка.
Изобразить точку на траектории, ее скорость и ускорение в заданный
момент времени. |
|
|
cos2πt = 2cos2 πt −1, |
Решение: 1. |
Используя формулу тригонометрии |
||
исключим время |
t из уравнений движения (26) и |
получим уравнение |
|
траектории движения точки: |
|
|
|
|
x = 0,828(y − 0,8)2 + 0,2 . |
(27) |
|
Траекторией точки является парабола. |
7 , получим координаты точки x , |
||
2. Подставляя в уравнение (26) t = t = |
|||
|
1 |
3 |
|
y в данный момент времени: x = 0,55см, y = 1,45см.
3. Найдем проекции скорости точки на оси координат Ox и Oy :
23

|
Vx |
= dx |
= -0,7sin 2πt × 2π = -1,4π sin 2πt , |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Vy |
= dy |
= -1,3sin πt ×π = -1,3π sinπt . |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
4. Найдем проекции вектора ускорения точки на оси Ox и Oy : |
||||||||||||||||||||||||||||||
|
ax |
= |
dVx |
= |
d 2x |
= -1,4π sin 2πt × 2π = -2,8π |
2 |
cos 2πt , |
|||||||||||||||||||||||
|
|
dt |
|
|
|
|
dt |
2 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
ay |
= |
dVy |
= |
|
|
d 2 y |
|
|
= -1,3π sin π ×π = -1,3π 2 cosπt . |
|||||||||||||||||||||
|
|
|
dt |
|
|
|
|
dt2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
5. Найдём проекции скорости и ускорения в момент времени |
||||||||||||||||||||||||||||||
|
t = t |
= |
7 |
|
c.: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Vx = −0,7 |
|
|
|
π ≈ −3,81 см/с, |
Vy = -0,65 |
|
π » -3,54 см/с, |
|||||||||||||||||||||||
|
|
|
3 |
3 |
|||||||||||||||||||||||||||
|
ax =1,4π 2 »13,82 см/с2, |
ay = −0,65π 2 ≈ −6,42 см/с2. |
|||||||||||||||||||||||||||||
|
6. Модули скорости и ускорения вычисляем по формулам: |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
V = |
|
V 2 +V 2 |
, a = |
|
a2 |
+ a2 |
, и при t = t имеем: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
x |
y |
|
1 |
|
|
|
|
||
|
V ≈ 5,20 см/с, |
|
|
|
|
|
a ≈ 15,24 см/с2. |
|
|
|
|
|
|||||||||||||||||||
|
7. |
|
Касательное |
|
ускорение |
aτ |
находим |
|
путем дифференцирования |
||||||||||||||||||||||
модуля скорости: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
a |
|
= |
|
dV |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(28) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
τ |
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
dV |
|
рекомендуется вычислять по формуле: |
|
|
||||||||||||||||||||||||||
|
dt |
|
|
|
|
|
Vxax +Vyay |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
dV |
= |
. |
|
|
|
|
|
|
(29) |
|||||||||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Для данного момента времени по формуле (29) найдем: |
||||||||||||||||||||||||||||||
|
dV |
|
= -5,76 см/с2. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dV |
|
|
|
|
|
|
|
|
|
|
Знак минус при |
показывает, |
что движение точки замедленное, и, |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
следовательно, вектор касательного ускорения направлен противоположно вектору скорости.
8. Используя формулу (28), получим касательное ускорение при t = t1: aτ ≈ 5,76 см/с2.
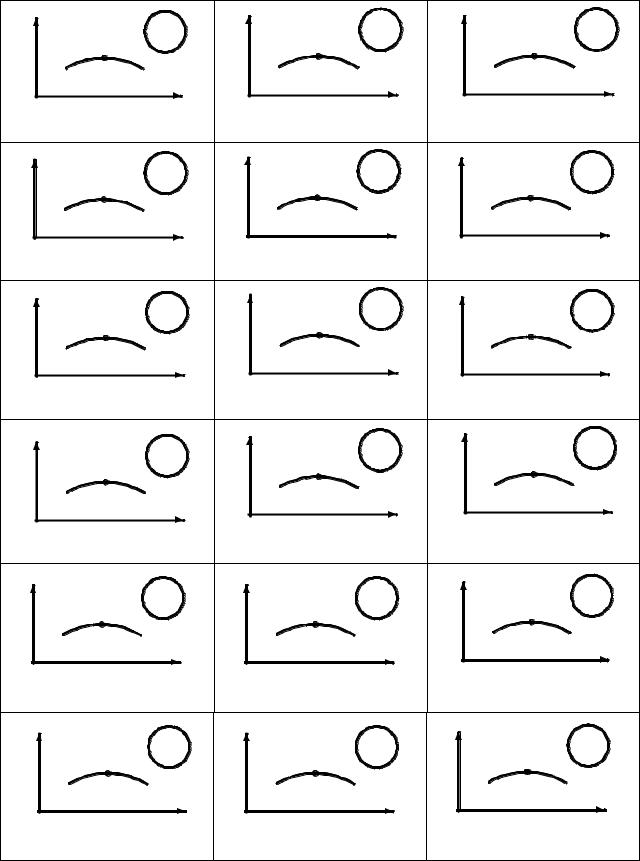
Нормальное ускорение точки при t = t1 вычислим по формуле: an = 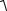
 a2 − aτ2 = 14,10 см/с2.
a2 − aτ2 = 14,10 см/с2.
24

9. Радиус кривизны траектории в той точке, |
где при t = t1 |
находится |
|||||||||
точка М , вычислим по формуле: |
|
|
|
|
|
|
|
||||
ρ = |
V 2 |
= 1,92 см. |
|
|
|
|
|
|
|
|
|
an |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
10. Пользуясь уравнением (27), изобразим траекторию и покажем на ней |
|||||||||||
положение точки М в |
заданный момент времени. Вектор V |
строим по |
|||||||||
составляющим Vx и Vy , |
причем этот вектор должен быть направленным по |
||||||||||
касательной к траектории точки. Вектор a находим как по составляющим ax |
|||||||||||
и ay , так и по aτ и an , чем контролируем |
правильность вычислений. |
|
|||||||||
Ответ: |
x = 0,55см, |
y = 1,45см, |
V ≈ 5,20 |
см/с, |
a ≈ 15,24 |
см/с2, |
|||||
a |
≈ 5,76 см/с2, a |
n |
= 14,10 см/с2, ρ =1,92 см. |
|
|
|
|
||||
τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
2 см /с |
3 см /с 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
a |
τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vx |
M |
|
|
a x |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
V |
Vy |
|
|
a |
|
|
|
|
|
|
|
a y |
|
|
|
|
|
||
|
|
|
|
|
1 |
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
0 |
|
|
a n |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.3.1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Таблица 3.1 |
||
№№ п/п |
|
|
|
А |
|
|
Б |
|
|
α1 |
α2 |
α3 |
|
α4 |
α5 |
α6 |
t1 |
|
(см) |
(см) |
(см) |
|
(см) |
(см) |
(см) |
(с) |
0 |
-0,6 |
0 |
0 |
|
0 |
0 |
2 |
2/3 |
1 |
0 |
0,3 |
0 |
|
0 |
0 |
2 |
3/4 |
2 |
0 |
0 |
0,4 |
|
0 |
0 |
1 |
5/6 |
3 |
2 |
0 |
0 |
|
0 |
0 |
-3 |
7/6 |
4 |
0 |
-4 |
0 |
|
0 |
0 |
2 |
5/4 |
5 |
3 |
0 |
0 |
|
0 |
0 |
-1 |
1/3 |
6 |
0 |
0 |
0 |
|
0,5 |
0 |
-2 |
4/3 |
7 |
0 |
0 |
0 |
|
0 |
-0,3 |
4 |
11/6 |
8 |
4 |
0 |
0 |
|
0 |
0 |
-2 |
5/3 |
9 |
-2 |
0 |
0 |
|
0 |
0 |
3 |
7/4 |
25
y |
|
1 |
y |
2 |
y |
3 |
|
M |
M |
M |
|||
|
|
|
|
|||
|
|
x |
|
x |
|
x |
O |
|
|
O |
|
O |
|
x = 0,9sinπt − 0.8 |
x =1,3cosπt |
x = −0,2cos2 πt − 3,1 |
||||
y |
|
4 |
y |
5 |
y |
6 |
|
M |
M |
M |
|||
|
|
|
|
|||
|
|
x |
|
x |
|
x |
O |
|
|
O |
|
O |
|
x = 0,2cos 2πt |
x = 0,2sinπt |
x = −0,6sinπt + 1,4 |
||||
y |
|
7 |
y |
8 |
y |
9 |
|
M |
M |
M |
|||
|
|
|
|
|||
|
|
x |
|
x |
|
x |
O |
|
|
O |
|
O |
|
x = −2,3cosπt + 2 |
x = −0,2cos2 πt + 3 |
x = −0,3sin2 πt + 2 |
||||
y |
|
10 |
y |
11 |
y |
12 |
|
M |
M |
||||
|
M |
|||||
|
|
|
|
|
|
|
|
|
x |
|
x |
|
x |
|
|
O |
|
O |
|
|
O |
|
|
|
|
||
|
|
|
|
|
|
|
x = −0,8cos2πt + 3 |
x = −0,7cosπt + 2,2 |
x = −0,3cos2 πt − 2,4 |
||||
y |
|
13 |
y |
14 |
y |
15 |
|
M |
M |
M |
|||
|
|
|
|
|||
|
|
x |
|
x |
|
x |
O |
|
|
O |
|
O |
|
x = −0,4sinπt + 2 |
x = 1,5cosπt − 3 |
x = 0,9sin2 πt |
||||
y |
|
16 |
y |
17 |
y |
18 |
|
M |
M |
M |
|||
|
|
|
|
|||
|
|
x |
|
x |
|
x |
O |
|
|
O |
|
O |
|
x = 0,5sinπt − 3 |
x = 1,4cosπt + 3,2 |
x = 0,8cos2 πt + 2,5 |
||||
|
|
|
Рис.3.2 |
|
|
|
|
|
|
26 |
|
|
|

y |
|
19 |
y |
|
20 |
y |
|
21 |
|
M |
|
M |
|
M |
|||
|
|
|
|
|
|
|||
|
|
x |
|
|
x |
|
|
x |
O |
|
|
O |
|
|
O |
|
|
x = −0,25cos 2πt + 2 |
x = −0,9sin2 πt +1,2 |
x = 0,5cos2πt + 2,4 |
||||||
y |
|
22 |
y |
|
23 |
y |
|
24 |
|
M |
|
M |
|
M |
|||
|
|
|
|
|
|
|||
|
|
x |
|
|
x |
|
|
x |
O |
|
|
O |
|
|
O |
|
|
x = −0,7cos2 πt − 2 |
x = 0,7cos2πt −1,8 |
x = −1,3sin2 πt + 2,3 |
||||||
y |
|
25 |
y |
|
26 |
y |
|
27 |
|
M |
|
M |
|
M |
|||
|
|
|
|
|
|
|||
|
|
x |
|
|
x |
|
|
x |
O |
|
|
O |
|
|
O |
|
|
x = −0,7cos2 πt − 2,1 |
x = −1,2sin2 πt − 3 |
x = −0,93cos 2πt + 2,5 |
||||||
y |
M |
28 |
y |
|
29 |
y |
|
30 |
|
|
M |
|
M |
||||
|
|
|
|
|
|
|||
O |
|
x |
|
|
x |
|
|
x |
|
|
O |
|
|
O |
|
|
|
x = 0,6cos 2πt − 3,2 |
x = 0,7cosπt + 1,2 |
x = 1,5sinπt − 1,3 |
||||||
|
|
|
|
Рис.3.3 |
|
|
|
|
27
ЗАДАНИЕ № 4 (Д2)
ПРИМЕНЕНИЕ ОБЩИХ ТЕОРЕМ ДИНАМИКИ ТОЧКИ И РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ ДЛЯ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК МЕХАНИЧЕСКОГО ДВИЖЕНИЯ
Цель задания: Приобрести навыки в применении теорем об изменении количества движения и кинетической энергии материальной точки, а также в использовании дифференциальных уравнений в естественных осях.
Приступая к выполнению задания, следует изучить теоретический материал: ([1] §§ 83, 84, 87-89, 133, 135; [2] §§ 46-48, 58-60, 62, 106, 107).
Вопросник-минимум для защиты задания №4 (Д2):
1)Сформулируйте аксиомы динамики.
2)Что называется количеством движения точки?
3)Что называется элементарным импульсом силы?
4)Какова размерность количества движения точки и импульса силы в различных системах единиц?
5)Сформулируйте теорему о количестве движения точки в дифференциальной и конечной формах.
6)Запишите различные формы выражения элементарной работы переменной силы.
7)Как выражается работа на конечном перемещении?
8)Чему равна работа силы тяжести и когда она положительна?
9)Чему равна работа силы упругости?
10)Что называется кинетической энергией материальной точки?
11)Сформулируйте теорему об изменении кинетической энергии материальной точки.
Постановка задачи: Шарик, принимаемый за материальную точку, движется из положения A внутри трубки, ось которой расположена в вертикальной плоскости.
Пренебрегая трением на криволинейных участках траектории, найти скорости vB и vC шарика в положениях B и C и давление шарика на стенку
трубки NC в положении C , а также величину, указанную в последнем
столбце таблицы 2.1.
В схемах 2, 3, 7, 8, 13, 19, 20, 22, 25, 28, 29 шарик, пройдя путь λ0 ,
отделяется от пружины.
28

Номер схемы взять по рисункам 4.3 – 4.7 согласно первому двузначному числу шифра. Второе четырехзначное число шифра в данном задании не используется.
Исходные данные приведены в таблице 4.1., где m - масса шарика; vA - начальная скорость шарика; t1 - время движения шарика на участке A B
(в схемах 1, 4, 5, 9, 15, 16, 17, 18, 23, 24, 27, 30) или на участке BД (в схемах 2, 3, 6-8, 10-14, 19-22, 25, 26, 28, 29); f - коэффициент трения скольжения шарика по стенке трубки; λ0,λ1 - начальное и конечное удлинение (или
укорочение) пружины соответственно; C - коэффициент жесткости пружины; h - наибольшая высота подъема шарика; S - путь, пройденный шариком до остановки.
ПОРЯДОК РАСЧЕТА И ПРИМЕР НА ВЫПОЛНЕНИЕ ЗАДАНИЯ №4 (Д2)
1.Изобразить на рисунке все силы, приложенные к материальной точке, т.е. задаваемые силы и реакции связей на каждом из участков.
2.Если на прямолинейном участке AB задано время действия сил, то
следует выбрать систему координат и применить теорему об изменении количества движения точки.
Если на участке AB заданы такие параметры, как радиус R или λ0
(путь пройденный шариком), то следует применить теорему об изменении кинетической энергии материальной точки и определить vB ,vC .
3.Для вычисления давления шарика на стенку канала в положении C
привлечь дифференциальные уравнения движения в естественных осях координат. Вначале на участке BC следует применить теорему об изменении кинетической энергии материальной точки и определить vC .
4.Для определения величин, указанных в последнем столбце таблицы 2.1, из условий конкретно поставленной задачи следует применить теорему
об изменении количества движения и об изменении кинетической энергии материальной точки.
Пример: Шарик массы m = 0,5кг начинает движение из точки А со
скоростью vA = 0,8м/с. На участке ВДЕ на шарик действует еще сила трения (коэффициент трения f = 0,1). В точке Д шарик начинает сжимать пружину жесткостью C =1000н/м.
Определить vB , vД , vC , λmax , приняв g = 9,81м/с2, α = 600 , β = 300 , λ0 = 0 . λmax - величина максимального сжатия пружины, λ0 - величина
начальной деформации пружины.
Решение: 1. На участке ACB движение шарика происходит под дей- ствием силы тяжести P ; на участке BД , кроме силы P , действует сила
29
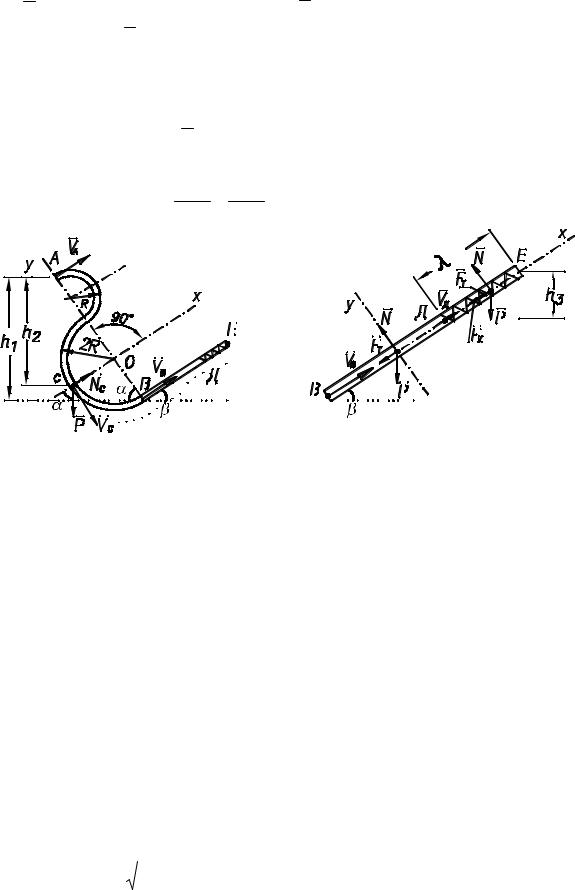
трения FT ; на участке ДЕ, кроме силы P и силы трения, действует сила упругости пружины Fy .
2. Для определения vB и vC применим теорему об изменении ки-
нетической энергии материальной точки.
Движение шарика на участках AB и AC траектории происходит под действием силы тяжести P (силу трения на криволинейных участках не учитываем);
mvB2 |
− mv2A = å Ak . |
(30) |
2 |
2 |
|
|
|
x |
|
|
a |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.2 |
|
|||||||||||||||||||||||||||||||||||||||||
Работу совершает только сила тяжести. Начальное положение шарика выше конечного, следовательно, работа будет положительной.
Работу силы тяжести вычисляем по формуле:
A = mgh1, (31) h1 = AB sin α = 6R sinα ,
|
|
|
|
|
mv |
2 |
|
|
mv2 |
|
|
A = mg6R sinα , итак |
|
B |
− |
A |
= mg6R sinα |
||||
2 |
|
|
2 |
|||||||
|
|
|
|
|
|
|
|
|
||
или vB2 − v2A =12gR sinα , h = 9,81 м/с2 |
; |
откуда vB = 4,59 м/с. |
||||||||
Для нахождения скорости шарика в точке C применяем теорему об |
||||||||||
изменении кинетической энергии точки на участке AC : |
||||||||||
|
mvC2 |
− mv A2 = å Ak , A = mgh2 , |
|
|
||||||
2 |
|
|
||||||||
2 |
|
|
|
|
|
|
||||
h2 = AO sin α + OC cos α = 4R sin α + 2R cos α , |
||||||||||
v2 |
− v2 = 2g(4R sin α + 2R cos α ) |
|
|
|||||||
|
C |
|
|
A |
|
|
|
|
|
|
и v |
= |
|
v2 + 4gR(2sinα + cosα ) |
|
|
|
||||
|
C |
|
|
A |
|
|
|
|
|
|
После подстановки числовых значений получаем: vC = 4,26 м/c.
30
