
Лекция 1 Неопр интеграл
.pdf1
Лекция 1. Неопределенный интеграл и его свойства.
В прошлом семестре мы рассмотрели следующую задачу: дана функция F(x) необходимо найти ее производную f (x) = F (x) .
Теперь будем рассматривать обратную задачу: дана производная F (x) = f (x) , требуется найти саму функцию F (x) .
С механической точки зрения это означает, что по известной скорости движения точки необходимо восстановить закон ее движения.
Определение 1. Функция F (x) называется первообразной от функции f (x) на интервале (a;b) , если во всех точках этого интервала F (x) дифференцируема
и F (x) = f (x) .
Пример1. Найти первообразную от функции f (x) =x4.
Из определения 1 |
следует, что F (x) = |
|
1 |
x5 |
является первообразной, так как |
||||||
5 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
1 |
|
5 |
|
4 |
|
|
|
|
|
||
|
|
|
|
=x . |
|
|
|
|
|
||
(5 x |
|
) |
|
|
|
|
|
||||
Теорема 1. Если |
F (x) - первообразная для |
f (x) на (a;b) , то F (x) +С тоже |
|||||||||
первообразная, где С – любое постоянное число ( С=const ).
Доказательство: (F(x) C) (F(x)) C f (x) .
Теорема 2. Если F1 (x) и F2 (x) - две первообразные для f (x) на (a;b) , то F1 (x) - F2 (x) =С на (a;b) , где С – любое постоянное число.
Доказательство: По условию F1 (x) = F2 (x) = f (x) для любого x (a;b) . Составим функцию (x) = F1 (x) - F2 (x) ,
очевидно, что (x) = F1 (x) - F2 (x) = f (x) - f (x) =0.
Но из равенства (x) =0 следует, что (x) есть постоянная. Следовательно, (x) =С или F1 (x) - F2 (x) =С, что и требовалось доказать.
Из этих теорем следует, что если данной функции f (x) найдена какая-нибудь одна первообразная F (x) , то любая другая первообразная для f (x) имеет вид
F (x) +С, где С=const.
Определение 2. Если F (x) является первообразной для f (x) , то выражение
F (x) +С, называется неопределенным интегралом от функции f (x) и
обозначается f (x)dx .
Таким образом, по определению f (x)dx = F (x) +С, если F (x) = f (x) . При этом, знак называют знаком интеграла,
функцию f (x) - подынтегральной функцией,
2
выражение f (x) dx – подынтегральным выражением.
Операцию нахождения неопределенного интеграла называют интегрированием функции. Таким образом проинтегрировать функцию значит найти все ее первообразные.
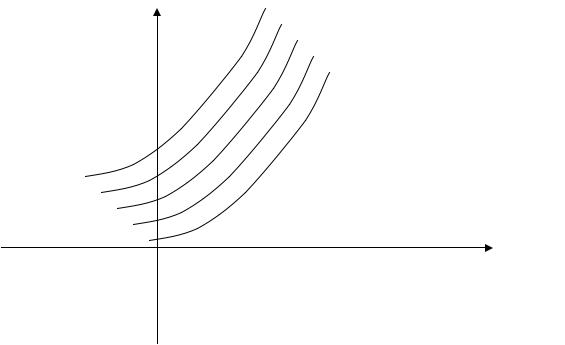
Неопределенный интеграл представляет собой семейство функций y= F (x) +С. Геометрически, это семейство кривых, каждая из которых получается путем сдвига вдоль оси Oy (Рис. 1).
y
O |
x |
Рис. 1
Эти кривые называют интегральными кривыми.
Естественно возникает вопрос, для всякой ли функции существует первообразная. Оказывается, что если f (x) непрерывна на (a;b) , то для нее существует первообразная на (a;b) , а, следовательно, и неопределенный интеграл.
Свойства неопределенного интеграла.
Свойство 1. Производная от неопределенного интеграла равна подынтегральной функции
( f (x)dx) = f (x) .
Действительно пользуясь определением 1, имеем
( f (x)dx) = (F(x) C) = f (x) .
Свойство 2. Дифференциал от неопределенного интеграла равен подынтегральному выражению
d ( f (x)dx) = f (x) dx.
В самом деле, f (x)dx = F (x) +С, тогда

|
3 |
|
|
d ( f (x)dx) =d(F(x)+C)= (F (x) C) |
dx F (x)dx = f (x) dx. |
Свойство 3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная.
dF (x) = F (x) +С.
По определению дифференциала функции dF(x)= F (x) dx, тогда имеем,
dF (x) = F (x)dx f (x)dx = F (x) +С.
Свойство 4. Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов
( f1 (x) f2 (x))dx = f1 (x)dx + f2 (x)dx .
По свойству 1
( ( f1 (x) f2 (x))dx) =f1(x)+f2(x).
С другой стороны
( f1 (x)dx + f2 (x)dx) = ( f1 (x)dx) + ( f2 (x)dx) = f1(x)+f2(x).
Так как производные слева и справа равны, то функции отличаются на постоянную величину. В этом смысле и следует понимать свойство 4.
Свойство 5. Постоянный множитель можно выносить за знак интеграла, т.е., если С=const, то
Сf (x)dx = С f (x)dx .
Для доказательства найдем производные от левой и правой части
( Сf (x)dx) =Сf(x),
(C f (x)dx) =C ( f (x)dx) =Cf(x).
Производные слева и справа равны, следовательно, функции стоящие слева и справа отличаются только на постоянную величину.
Таблица интегралов.
Запишем таблицу интегралов, вытекающую из основных формул дифференцирования:
1. 0dx C.
2.xn dx nx 1 C , при n 1.
3.x 1dx = dxx =ln|x|+C, при x 0.n 1
4. |
a x dx = |
a x |
C , при a (0;1) (1; ) , в частности, |
e x dx =ex+C. |
|
ln a |
|||||
|
|
|
|
||
5. |
sin xdx =-cosx+C, cos xdx =sinx+C. |
|
|||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
6. |
|
|
dx |
|
= tgx+C, |
|
|
|
dx |
|
= - ctgx+C. |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
cos |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
x |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
C, |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
arcsin |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
||||||||||||||||||||||||
7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
, при x ( a; a). |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||||||||||||||||||
|
|
a 2 |
x2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
arccos |
|
C, |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
arctg |
x |
|
C, |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
8. |
|
|
|
|
|
|
= |
|
a |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
a 2 x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a arcctg a C. |
|
|
|
||||||||||||||||||||||
9. |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
= ln | x |
|
|
x |
2 |
a | C. |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
x |
2 |
a |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
10. |
|
|
dx |
|
= |
|
1 |
ln | |
|
x a |
| . |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
x |
2 2 |
|
|
|
|
|
x a |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
a |
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Докажем формулу 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
x, еслиx 0, |
, то при x 0 |
|
1, еслиx 0, |
|
||||||||||||||||||||||||||||||||
Так как |x|= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
=signx, кроме того, |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| x | |
|||||||||||||||||||||||||
|
|
|
|
|
|
x, еслиx 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, еслиx 0 |
|
||||||||||||||||||
1, еслиx 0,
|x| signx =|x| =x.
1, еслиx 0
Тогда дифференцируя правую часть формулы 3 как сложную функцию, получаем
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
, при x 0. Формула 3 доказана. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
(ln | x | C) |
= | x | |
| x | |
= |
| x | signx = x |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Докажем еще формулу 9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||
(ln | x x |
|
|
a | |
C) |
= |
|
|
|
|
|
|
|
|
|
|
|
| x |
|
x |
|
a | |
= |
|
|
|
|
|
|
|
|
(signx |
|
|
x |
|
a ) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| x x2 |
a | |
|
|
|
|
|
|
|
|
| x |
|
|
x2 a | |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
x2 a |
x |
= |
|
|
1 |
. |
|
|||||||||||
(x x2 a ) = |
|
|
|
|
|
|
(1 |
|
|
|
2x) = |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
x x2 a |
2 x2 a |
|
|
|
|
x |
x2 a |
|
|
|
|
x2 a |
|
x 2 a |
|||||||||||||||||||||||||||||||
Следует отметить, что если операция дифференцирования элементарных функций снова приводит к элементарным функциям, то операция интегрирования уже может привести к неэлементарным функциям.
Например, интеграл Пуассона e x2 dx не интегрируется в элементарных функциях.
Табличное интегрирование. |
|
|
||
Пример 2.Вычислить интеграл (6x2 |
8x 3)dx . |
|
||
Применив свойство 4, получим (6x2 |
8x 3)dx = 6x2 dx + 8xdx + 3dx . |
|||
Применив |
свойство |
5, получим |
(6x2 8x 3)dx = |
6 x2 dx +8 xdx +3 dx . |
Применив |
свойство 3, |
получим dx =x+C. Применив, |
формулу 2 таблицы |
|
интегралов окончательно получаем:

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
(6x2 |
|
8x 3)dx =6 |
x3 |
+8 |
x 2 |
+3x+C=2x3+4x2+3x+C. |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 3. Вычислить интеграл |
|
dx |
|
. |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
3x2 5 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
dx |
|
= |
dx |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
5 |
3(x 2 |
|
5 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Применив свойство 5, получим |
|
|
dx |
= |
1 |
|
dx |
|
|
|
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
3x |
2 |
5 |
3 |
x 2 |
5 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Применив, формулу 8 таблицы интегралов, где a2= |
5 |
окончательно получаем: |
||||||||||||||||||||||||||||||||
3 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
dx |
1 |
|
1 |
|
|
|
|
|
x |
|
|
|
|
1 |
|
|
|
|
3x |
|
|
|
|||||||||||
|
= |
|
|
|
|
|
|
|
|
|
arctg |
|
|
|
|
|
|
+C= |
|
|
|
|
arctg |
|
|
|
|
|
+C. |
|
|
|||
3x 2 5 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
5 |
|
|
|
|
5 |
|
|
|
|
|
15 |
|
5 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Вычислить интеграл |
|
|
dx |
|
|
|
|
|
|
|
|
|||||||||||||||||
Пример 4. |
|
. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
x 2 9 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Применив, формулу 10 таблицы интегралов, где вместо a надо подставить 3,
получаем |
dx |
|
1 |
|
x 3 |
|
1 x 3 |
|
||
|
= |
|
ln| |
|
|+C= |
|
ln| |
|
|+C. |
|
x 2 9 |
2 3 |
x 3 |
6 |
x 3 |
||||||
Часто при вычислении интегралов используют прием подведения под знак дифференциала. В нем используют, что
dx= |
1 |
d(kx+b), где k,b – числа. |
|||||||||||
|
|||||||||||||
|
k |
|
|
|
|
|
|
|
|
|
|
||
Пример 5. . Вычислить интеграл |
5dx |
|
|
|
|||||||||
|
|
. |
|
|
|
||||||||
4 x |
|
|
|
||||||||||
Применив свойство 4, получим |
|
5dx |
=-5 |
|
dx |
. |
|||||||
|
|
|
|||||||||||
|
|
|
|
|
4 x |
|
x 4 |
||||||
Так как dx=d(x-4), то |
|
5dx |
=-5 |
d (x 4) |
. |
|
|
|
|||||
|
|
|
4 x |
|
|
x 4 |
|
|
|
||||
Применив, формулу 3 таблицы интегралов, где вместо x надо подставить (x-
4), окончательно получаем |
5dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
=-5ln|x-4|+С. |
|
|
|
|
|
|
|
||||||||||||
4 x |
|
|
|
|
|
|
|
||||||||||||||
Пример 6. Вычислить интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 3xdx . |
|
|
|
|
|
|
|
|||||||||||||
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|||||||
|
d(2-3x), то |
|
|
= (2 3x) |
|
( |
d (2 3x)) . |
||||||||||||||
Так как dx=- |
2 3xdx |
2 |
|||||||||||||||||||
|
|
|
|||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
||||
Применив свойство 5, получим |
|
|
|
|
|
(2 3x) |
|
d (2 3x) . Применив, |
|||||||||||||
|
|
2 3xdx = - |
|
2 |
|||||||||||||||||
|
|
|
3 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
формулу 2 таблицы интегралов, |
|
где вместо |
x надо подставить (2-3x), |
||||||||||||||||||

6
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
(2 3x) 32 |
|
|
2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
=- |
|
|
+С= - |
|
|
|
(2 3x)3 |
|
|||||||||||||
окончательно получаем |
2 3xdx |
|
|
|
+С. Пример |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
9 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
7. Вычислить интеграл (5x4 e1 x sin 2x)dx . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Последовательно |
применив |
все |
|
|
|
выше |
изложенное, |
получаем |
|||||||||||||||||||||||||
(5x4 e1 x sin 2x)dx = 5x4 dx + e1 x dx - sin 2xdx = |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
=5 x4 dx + e1 x (d (1 x)) - sin 2x( |
1 |
d (2x)) =5 |
x5 |
- e1 x d (1 x)) |
- |
1 |
sin 2xd (2x) |
||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
2 |
|
|
|||||||||||
=x5-e1-x- |
1 |
(-сos2x)+C =x5-e1-x+ |
1 |
сos2x+C. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 8. Вычислить интеграл 23x 1dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
23x 1dx = 23x 1 ( |
1 |
d (3x 1)) = |
|
1 |
23x 1d (3x 1) |
= |
1 |
|
23x 1 |
|
+С= |
23x 1 |
|
+С. |
|
||||||||||||||||||
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
3 |
|
ln 2 |
|
|
ln 8 |
|
|
|
|
|
|
||||||||
