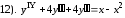Задание 8

Найти общее решение дифференциального уравнения

1. 

2. 

3. 

4. 

5. 

Задание 9

Найти общее решение дифференциального уравнения

Задание 10

Найти общее решение дифференциального уравнения

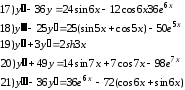
Задание 11

Найти решение задачи Коши

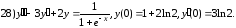
3. Линейные системы с постоянными коэффициентами

Система линейных дифференциальных уравнений с постоянными коэффициентами (однородная или неоднородная) всегда может быть проинтегрирована путем сведения ее к одному уравнению высшего порядка.

Пример 1. Найти общее решение системы

Решение. Продифференцируем первое уравнение системы: . В правую часть полученного равенства подставим выражение дляиз второго уравнения системы:Выразимиз первого уравнения системы

(3.1)

Тогда для отыскания получим неоднородное уравнение

Корни характеристического уравнения . Поэтому общее решение соответствующего однородного уравнения имеет вид

.

Частное решение неоднородного уравнения ищем в виде Используя стандартные приемы, находим:Итак,

Используя формулу (3.1), получаем

Изложенный метод удобен только для решения несложных систем. В общем случае для решения линейных систем может быть использован "матричный метод".

Пусть имеется линейная система

(3.2)

где постоянная матрица,. Обозначим черезсобственные значения матрицы.

Если все собственные значения матрицы различны, то общее решение системы (3.2) имеет вид

, (3.3)

где собственные векторы, соответствующие указанным собственным значениям.

Пример 2. Найти общее решение системы

Решение. Составим характеристическое уравнение

Ненулевые собственные векторы , соответствующие найденным собственным значениям, могут быть найдены как алгебраические дополнения элементов любой строки матрицы. Так, например, в качестве собственного вектора, соответствующего собственному значению, возьмем алгебраические дополнения элементов первой строки матрицы

.

Аналогично находим

.

Поэтому, согласно формуле (3.3), общее решение системы имеет вид

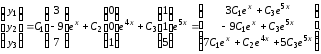
Если среди различных корней характеристического уравнения имеются комплексно-сопряженные , то каждой такой паре корней соответствуют два комплексных решения, гдеи– комплексные собственные векторы. Комбинируя эти решения, легко получить два решения в вещественной форме. В качестве таких решений можно взять,.

Если среди корней характеристического уравнения имеется корень кратности, то этому корню соответствует решение вида

(3.4)

Для нахождения значений неизвестных коэффициентов нужно подставить выражение (3.4) в систему (3.2) и приравнять коэффициенты при одинаковых степеняхв левой и правой частях получившихся равенств. При этом следует помнить, что ровноиз отыскиваемых коэффициентов могут быть выбраны произвольно, а остальные должны быть выражены через них.

Пример 3. Найти общее решение системы

Решение. Характеристическое уравнение

или

имеет корни .

Простому собственному значению соответствует собственный вектори решение вида

. (3.5)

Решение, соответствующее двукратному корню , в соответствии с формулой (3.4), будем искать в виде

Получаем уравнение

или

Приравнивая коэффициенты при одинаковых степенях в левой и правой частях последнего равенства, получим систему уравнений

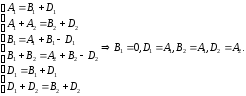
Считая – произвольными постоянными, окончательно находим

Складывая, наконец, последнее выражение с (3.5), получаем общее решение системы