
- •1. Уравнения первого порядка
- •1.1.Уравнения с разделяющимися переменными и уравнения, приводящиеся к ним
- •1.2. Геометрические и физические задачи
- •Задание 11
- •1.3. Однородные уравнения и уравнения, приводящиеся к ним
- •Задание 2
- •1.4. Линейные уравнения, уравнения Бернулли и уравнения Риккати
- •Задание 3
- •1.5. Уравнения в полных дифференциалах. Интегрирующий множитель
- •Задание 4
- •1.6. Уравнения, не разрешенные относительно производной. Особые решения
- •Задание 5
- •1.7. Существование и единственность решения задачи Коши. Метод последовательных приближений
- •Задание 6
- •2. Дифференциальные уравнения n-го порядка
- •2.1. Методы интегрирования некоторых классов дифференциальных уравнений, допускающих понижение порядка
- •Задание 7
- •2.2. Линейные уравнения с постоянными коэффициентами
- •Задание 8
- •3.1 Матричная экспонента
- •3.2. Формула Коши
- •Задание 12
- •Задание 13
- •Задание 14
- •Библиографический список
Задание 3
В задачах 1 -9 найти решения, удовлетворяющие заданным условиям



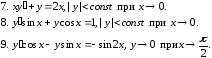
Решить уравнения.
|
|
|
|
|
|
1.5. Уравнения в полных дифференциалах. Интегрирующий множитель
Уравнение
 (1.10)
(1.10)
называется
уравнением в
полных дифференциалах,
если
 – дифференцируемые функции, для которых
– дифференцируемые функции, для которых
 ,
(1.11)
,
(1.11)
причем производные
в (1.11) непрерывны в некоторой области,
содержащей точку
 .
.
При выполнении
условия (1.11) (и только в этом случае)
левая часть уравнения (1.10) является
полным дифференциалом некоторой функции
двух переменных
 :
:
 .
(1.12)
.
(1.12)
Поэтому уравнение
(1.10) имеет вид
 и его общий интеграл –
и его общий интеграл – .
.
Функция
 может быть найдена по формуле
может быть найдена по формуле
 ,
(1.13)
,
(1.13)
или непосредственно исходя из справедливости соотношения (1.12).
Пример 1. Решить уравнение

Решение. Это уравнение в полных дифференциалах, поскольку

Функцию
 найдем из уравнений
найдем из уравнений

Интегрируя,
например, второе из этих уравнений по
 (считая
(считая постоянным), получаем
постоянным), получаем

где
 – некоторая дифференцируемая функция.
Подберем эту функцию так, чтобы
выполнялось соотношение
– некоторая дифференцируемая функция.
Подберем эту функцию так, чтобы
выполнялось соотношение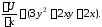 Имеем
Имеем

Итак,
 и общий интеграл уравнения имеет вид
и общий интеграл уравнения имеет вид
Если условие (1.11)
не выполнено, то уравнение (1.10) не будет
уравнением в полных дифференциалах.
Можно попытаться найти функцию
 (интегрирующий множитель) так, чтобы
уравнение
(интегрирующий множитель) так, чтобы
уравнение
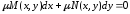
стало уравнением в полных дифференциалах. Для этого должно выполняться условие
 или
или
 (1.14)
(1.14)
Предположим, что
интегрирующий множитель является
функцией только переменной
 Тогда уравнение (1.14) принимает вид
Тогда уравнение (1.14) принимает вид
 .
(1.15)
.
(1.15)
Если правая часть
уравнения в (1.15) есть функция, зависящая
только от
 ,
то интегрирующий множитель вида
,
то интегрирующий множитель вида существует.
существует.
Аналогично получаем,
что в случае, когда выражение
 есть функция, зависящая только от
есть функция, зависящая только от ,
существует интегрирующий множитель
вида
,
существует интегрирующий множитель
вида ,
который находится из уравнения
,
который находится из уравнения
 (1.16)
(1.16)
Пример 2.
Решить уравнение

Решение. Представим данное уравнение в виде
 (1.17)
(1.17)
Заметим, что
 .
.
Поэтому существует
интегрирующий множитель вида
 ,
который может быть найден из уравнения
(1.16):
,
который может быть найден из уравнения
(1.16):

В качестве
 возьмем
возьмем .
Умножая обе части уравнения (1.17) на
.
Умножая обе части уравнения (1.17) на ,
получим уравнение в полных дифференциалах
,
получим уравнение в полных дифференциалах

Функцию
 найдем по формуле (1.13), взяв
найдем по формуле (1.13), взяв :
:

Итак, общий интеграл
уравнения имеет вид
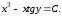 Заметим, что при делении на
Заметим, что при делении на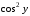 потеряны решения исходного уравнения
потеряны решения исходного уравнения
Задание 4
Решить уравнения, убедившись предварительно, что они являются уравнениями в полных дифференциалах




Решить уравнения,
допускающие интегрирующий множитель
вида
 или
или





1.6. Уравнения, не разрешенные относительно производной. Особые решения
Дифференциальное уравнение первого порядка, не разрешенное относительно производной, имеет вид
 (1.18)
(1.18)
Для решения
уравнения (1.18) желательно разрешить его
относительно
 .
При этом может получиться несколько
уравнений
.
При этом может получиться несколько
уравнений ,
разрешенных относительно производной.
Если удается найти решения всех этих
уравнений, то, объединяя их, получим
общее решение уравнения (1.18) .
,
разрешенных относительно производной.
Если удается найти решения всех этих
уравнений, то, объединяя их, получим
общее решение уравнения (1.18) .
Решить уравнение

Решение. Представим
данное уравнение в виде
 Следовательно, данное уравнение
эквивалентно совокупности двух уравнений:
Следовательно, данное уравнение
эквивалентно совокупности двух уравнений: и
и Решения первого из них
Решения первого из них и
и .
Решение второго
.
Решение второго Окончательно получаем, что общее решение
исходного уравнения
Окончательно получаем, что общее решение
исходного уравнения
Однако уравнение
(1.18) не всегда удается разрешить
относительно
 .
Часто разрешенное относительно
.
Часто разрешенное относительно уравнение плохо интегрируется. В
некоторых случаях уравнение (1.18) удобнее
интегрировать методомвведения
параметра.
уравнение плохо интегрируется. В
некоторых случаях уравнение (1.18) удобнее
интегрировать методомвведения
параметра.
Пусть, например,
уравнение (1.18) легко разрешается
относительно
 .
Введем параметр
.
Введем параметр .
Тогда уравнение примет вид
.
Тогда уравнение примет вид .
Дифференцируя обе части последнего
равенства по
.
Дифференцируя обе части последнего
равенства по ,
получим
,
получим .
Если удается разрешить это уравнение
относительно
.
Если удается разрешить это уравнение
относительно ,
то есть найти
,
то есть найти ,
то получим решение исходного уравнения
в параметрической форме:
,
то получим решение исходного уравнения
в параметрической форме:

Пример 2. Решить
уравнение
 .
.
Решение.
Введем параметр
 Тогда
Тогда

 или
или
 .
.
Получаем, что
 или
или .
Значению
.
Значению соответствует решение
соответствует решение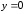 .
.
Итак, решениями
исходного уравнения являются
 и
и
Пусть уравнение
(1.18) может быть разрешено относительно
х:
 .
В этом случае уравнение может быть
решено с использованием подстановки
.
В этом случае уравнение может быть
решено с использованием подстановки
Пример 3.
Найти общее решение уравнения

Решение.
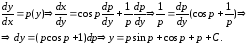
Итак, параметрические уравнения решения имеют вид

Как и уравнение, разрешенное относительно производной, уравнение (1.18) может иметь особые решения, то есть решения, целиком состоящие из особых точек (точек неединственности). Особые решения, если они имеются, удовлетворяют системе уравнений
 (1.19)
(1.19)
Для каждой функции
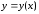 ,
удовлетворяющей системе (1.19), необходимо
проверить, что она в самом деле является
решением уравнения (1.18) и является особым
решением, то есть в каждой точке кривой
,
удовлетворяющей системе (1.19), необходимо
проверить, что она в самом деле является
решением уравнения (1.18) и является особым
решением, то есть в каждой точке кривой ее касаются другие интегральные кривые
того же уравнения.
ее касаются другие интегральные кривые
того же уравнения.
Особым решением
дифференциального уравнения (1.18) будет
являться и огибающая
семейства
 интегральных кривых этого уравнения.
Для нахождения огибающей семейства
интегральных кривых
интегральных кривых этого уравнения.
Для нахождения огибающей семейства
интегральных кривых следует исключить параметр
следует исключить параметр из системы уравнений
из системы уравнений
 (1.20)
(1.20)
и проверить, является ли полученная кривая огибающей, то есть, касаются ли ее в каждой точке кривые данного семейства.
Пример 4. Решить
уравнение
 .
Найти его особые решения (если они есть).
.
Найти его особые решения (если они есть).
Решение. Положив
 ,
получим
,
получим

 .
То есть
.
То есть или
или .
Поэтому решениями исходного уравнения
являются функции
.
Поэтому решениями исходного уравнения
являются функции

Исключая параметр
 ,
имеем
,
имеем .
.
Найдем теперь решения, "подозрительные" на особые. Система (1.19) в данном случае принимает вид

Исключая из нее
 ,
найдем:
,
найдем: .
Проверим, является ли решение
.
Проверим, является ли решение особым, то есть проверим касаются ли
его кривые семейства решений
особым, то есть проверим касаются ли
его кривые семейства решений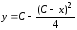 .
Условия касания кривых
.
Условия касания кривых и
и в точке с абсциссой
в точке с абсциссой выглядят так:
выглядят так: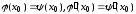 .
В данном случае они примут вид
.
В данном случае они примут вид

Исключая
 из этой системы, получаем
из этой системы, получаем .
Это равенство справедливо при всех
.
Это равенство справедливо при всех .
Последнее и означает, что
.
Последнее и означает, что – особое решение.
– особое решение.
Заметим, что это же особое решение могло быть найдено из системы (1.20), которая в данном случае имеет вид












