1.3. Однородные уравнения и уравнения, приводящиеся к ним

Функция называетсяоднородной степени k, если

Однородным называется уравнение, которое может быть приведено в виду , а также уравнение, в котороми– однородные функции одинаковой степени однородности. Чтобы решить однородное уравнение, нужно сделать замену. После такой замены получим уравнение с разделяющимися переменными.

Уравнение вида приводится к однородному с помощью замены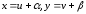, гдеиявляются решением системы

Если определитель этой системы равен нулю, то уравнение сразу приводится к уравнению с разделяющимися переменными заменой .

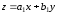Пример 1. Решить уравнение

Решение. Приведем уравнение к виду

Выполним замену . После преобразований и разделения переменных получим

.

Возвращаясь к исходным переменным, будем иметь . Это общий интеграл исходного уравнения. Заметим, что при разделении переменных могли быть потеряны решения. Непосредственная проверка показывает, что это действительно решения уравнения. Поэтомуи– решения исходного уравнения, не входящие в найденный общий интеграл.

Пример 2. Решить уравнение .

Решение. Уравнение приводится к однородному заменой 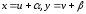, гдеиявляются решением системы

Итак, выполним замену Получим однородное уравнениеПолагая в этом уравнении, последовательно получим

Так как обращается в ноль прии, то функциии– решения дифференциального уравнения. Остальные решения уравнения найдем, разделяя переменные

Возвращаясь к исходным переменным, получим

–общий интеграл уравнения.

Функциям ив переменныхисоответствуют решения исходного уравненияи. Решениесодержится в общем интеграле и получается из него при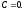

Задание 2

Решить уравнение. Найти общее или частное решение.

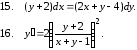
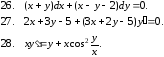
1.4. Линейные уравнения, уравнения Бернулли и уравнения Риккати

Линейным называется уравнение вида

(1.5)

где и– заданные непрерывные функции. Уравнение вида

(1.6)

называется уравнением Бернулли.

Уравнения (1.5) и (1.6) могут быть проинтегрированы с использованием одного и того же приема (метода Бернулли), который состоит в следующем: решения уравнений предлагается искать в виде произведения двух дифференцируемых функций . Подставляя выражения дляив левые части уравнений (1.5) или (1.6), получим соответственно

(1.7)

В качестве функции возьмем какое-либо решение уравненияНапример,Подставив найденное значениев (1.7), получим уравнение для отыскания функции.

Уравнением Риккати называется уравнение вида

(1.8)

где ,,– заданные непрерывные функции.

Заметим, что при уравнение (1.8) является уравнением Бернулли.

Если известно частное решение 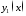уравнения Риккати, то подстановкой

. (1.9)

где – новая неизвестная функция, уравнение (1.8) приводится к уравнению Бернулли.

Частное решение , как правило, ищется подбором, чтобы будет продемонстрировано в приведенном ниже примере 3.

Пример 1. Найти решение уравнения , которое остается ограниченным при.

Решение. Решение уравнения ищем в виде . Имеем

Пусть – решение уравненияНапример,Функциюнайдем из уравнения, или. Тогда

Для ограниченного при решения имеем:ТогдаЗначит,Итак, искомое решение имеет вид

Пример 2. Решить уравнение

Решение. Запишем уравнение в виде 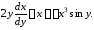Полученное уравнение является уравнением Бернулли , в котором роль независимой переменной играет. Решение этого уравнения будем искать в видеПодставляя в уравнение, получим. Функциюнайдем из уравненияДля отыскания функцииполучим уравнение

Итак, – общее решение уравнения. Заметим, что функция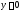также является решением этого уравнения.

Пример 3. Решить уравнение .

Решение. Будем искать частное решение в виде . Подставляяв уравнение, получаем

или .

Полагая , приходим к уравнению Бернулли. Сделав замену, получим. Функциюнайдем из уравненияДля отыскания функцииполучим уравнение

Значит, 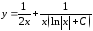– общее решение уравнения.