Задание 5

Найти все решения данных уравнений. Выделить особые решения (если они есть)

Уравнения 13 - 30 решить методом введения параметра. Найти особые решения (если они есть).

1.7. Существование и единственность решения задачи Коши. Метод последовательных приближений

Укажем условия существования и единственности решения задачи Коши (1.2) – (1.3).

Теорема Пикара-Линделефа. Пусть функция непрерывна на множествеи удовлетворяет условию Липшица поравномерно относительно, то есть существует такая постояннаяL>0 ,что для ивыполнено соотношение

Пусть М является верхней границей для на, а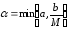. Тогда задача Коши

имеет на отрезке единственное решение.

Решение задачи Коши при выполнении условий теоремы Пикара-Линделефа может быть найдено как предел приравномерно сходящейся последовательности функций, определяемых рекуррентными соотношениями

(1.21)

Оценка погрешности при замене точного решения -ым приближениемможет быть выражена неравенством

(1.22)

Заметим, что если функция 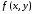имеет непрерывную частную производнуюв области, то значение постоянной ЛипшицаL может быть определено так: .

Пример 1. Найти область, в которой уравнение 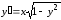имеет единственное решение.

Решение. Здесь . Функцияопределена и непрерывна при. Частная производнаянепрерывна и ограничена при. Следовательно, данное уравнение имеет единственное решение в любой полосе

Пример 2. Для задачи Коши указать какой-либо интервал существования решения. Найти это решение методом последовательных приближений, ограничившись приближениямии оценить ошибку третьего приближения.

Решение. Рассмотрим прямоугольник . На множестве. Поэтому интервал существования решения. Значит, решение существует прии на этом же интервале сходятся последовательные приближения. Последовательные приближения найдем по формуле (1.21):

Оценим теперь ошибку третьего приближения, пользуясь формулой (1.22). В качестве значения постоянной L можно взять верхнюю границу для наG: Поэтому.

Задание 6

Указать какой-нибудь отрезок, на котором существует решение с данными начальными условиями:

Построить последовательные приближения к решению данного уравнения с данными начальными условиями, указать какой-либо интервал, на котором сходится последовательность приближений:

Для следующих уравнений построить третье приближение в заданной области (или на заданном интервале) и оценить его ошибку.

Для следующих уравнений выделить области на плоскости (x,y),в которых через каждую точку проходит единственное решение уравнения.

2. Дифференциальные уравнения n-го порядка

Дифференциальное уравнение вида

называется дифференциальным уравнением -го порядка не разрешенным относительно старшей производной. Если удается разрешить его относительно, то получаем

. (2.1)

Теорема Коши (существования и единственности решения). Пусть функция , рассматриваемая как функция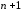переменной, непрерывна в некоторой области, содержащей точку, вместе со своими частными производными. Тогда существует интервали определенная на немn раз дифференцируемая функция , удовлетворяющая уравнению (2.1) и начальным условиям

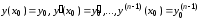. (2.2)

Функция , обладающая указанными свойствами, единственна.

Определение. Общим решением уравнения (2.1) (удовлетворяющего условиям теоремы Коши) называется функция , зависящая отx и n произвольных постоянных , такая, что

1. для любых значений произвольных постоянных функцияесть решение уравнения (2.1);

2. существуют единственные значения такие, чтоесть решение уравнения (2.1), удовлетворяющее начальному условию (2.2).

Если общее решение в области задано неявно соотношением

,

то оно называется общим интегралом уравнения.

Любое решение, получающееся из общего при конкретных значениях произвольных постоянных , называетсячастным решением.