
- •Министерство образования и науки Российской Федерации
- •Задание
- •«Численные методы»
- •Министерство образования и науки Российской Федерации
- •Содержание
- •Введение
- •Историческая справка
- •Вычисление интеграла в пространстве методом Монте-Карло Детерминистический метод
- •Обычный метод Монте-Карло
- •Геометрический метод
- •Вычисление кратных интегралов в пространстве методом Монте-Карло Обычный метод Монте-Карло
- •Заключение
- •Приложения Текст программы «Вычисление интеграла методом Монте-Карло»
- •Результат работы программы
- •Список литературы
Вычисление интеграла в пространстве методом Монте-Карло Детерминистический метод
Пусть
в пространстве
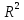 на
на
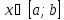 задана
функция
задана
функция
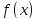 ,
причём
,
причём
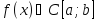 ,
,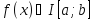 хотя бы один раз. Смысл метода состоит
в аппроксимации до элементарных фигур
разбиения. Разобьём
хотя бы один раз. Смысл метода состоит
в аппроксимации до элементарных фигур
разбиения. Разобьём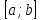 наn
частей, т.е.
наn
частей, т.е.
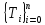 :
:
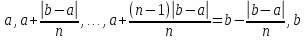 ,
где
,
где
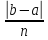 - длина приращения при равномерном
распределении. Рассмотрим два случая:
когда элементарные фигуры – трапеции,
и когда – прямоугольники.
- длина приращения при равномерном
распределении. Рассмотрим два случая:
когда элементарные фигуры – трапеции,
и когда – прямоугольники.
Трапеции.
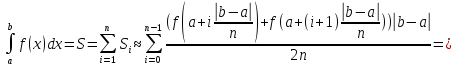
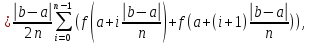
где
S
– площадь под графиком,
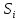 – площади разбиений графика, которые
аппроксимируем до трапеций.
– площади разбиений графика, которые
аппроксимируем до трапеций.
Пример: численно вычислить интеграл
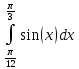
Решение
Сначала вычислим интеграл с помощью формулы Ньютона-Лейбница.
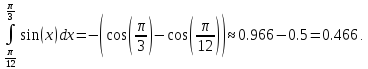
Пусть n=5, то
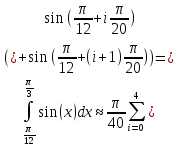
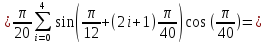
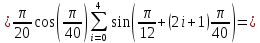
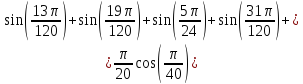
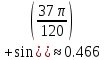
Из
полученного результата мы видим, что
при разбиении на 5 частей, с точностью
до
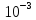 мы получаем исходный результат, что
говорит об актуальной применимости
детерминистического метода Монте-Карло
при разбиении на трапеции.
мы получаем исходный результат, что
говорит об актуальной применимости
детерминистического метода Монте-Карло
при разбиении на трапеции.
Прямоугольники.
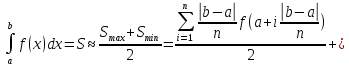
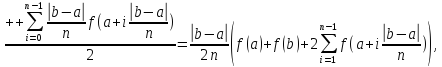
где
S
– площадь под графиком,
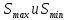 – соответственно площади разбиений
графика на прямоугольники с избытком
и недостатком.
– соответственно площади разбиений
графика на прямоугольники с избытком
и недостатком.
Пример: численно вычислить интеграл
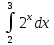
Решение
Сначала вычислим интеграл с помощью формулы Ньютона-Лейбница.
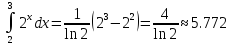
Пусть n=5, то
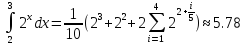
Из
полученного результата мы видим, что
при разбиении на 5 частей, с точностью
до
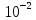 мы получаем исходный результат, что
говорит об актуальной применимости
детерминистического метода Монте-Карло
при разбиении на прямоугольники.
мы получаем исходный результат, что
говорит об актуальной применимости
детерминистического метода Монте-Карло
при разбиении на прямоугольники.
Обычный метод Монте-Карло
Пусть
в пространстве
 на
на
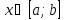 задана
функция
задана
функция
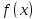 ,
причём
,
причём
 ,
, хотя бы один раз. Требуется найти площадь
под графиком этой функции на заданном
промежутке, то есть
хотя бы один раз. Требуется найти площадь
под графиком этой функции на заданном
промежутке, то есть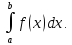
Рассмотрим
случайную величину p,
заданную на промежутке
 .
Очевидно, что
.
Очевидно, что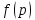 тоже случайная величина. Тогда запишем
формулу для её математического ожидания:
тоже случайная величина. Тогда запишем
формулу для её математического ожидания:
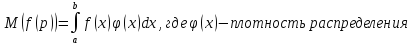
случайной
величины p,
причём
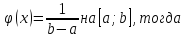
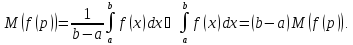
Разобьём
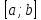 наn
частей, т.е.
наn
частей, т.е.
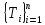 :
:
 ,
где
,
где
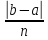 - длина приращения при равномерном
распределении. Тогда математическое
ожидание можно оценить следующим
образом:
- длина приращения при равномерном
распределении. Тогда математическое
ожидание можно оценить следующим
образом:
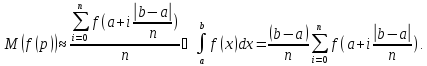
Пример: численно вычислить интеграл
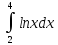
Решение
Сначала вычислим интеграл с помощью формулы Ньютона-Лейбница.
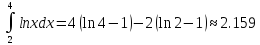
Пусть n=5, то
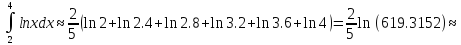
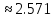
Пусть n=10, то

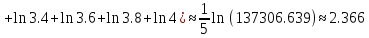
Из
полученного результата мы видим, что
при увеличении разбиений в два раза,
точность результата приблизилась к
настоящему на 0.205. При увеличении
разбиений результат приблизится к
исходному достаточно быстро, с точностью
до
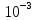 можно получить уже приn=50.
можно получить уже приn=50.
Геометрический метод
Пусть
в пространстве
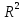 на
на
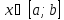 задана
функция
задана
функция
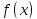 ,
причём
,
причём
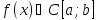 ,
,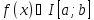 хотя бы один раз и на
хотя бы один раз и на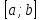
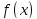 имеет
имеет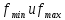 .
Разобьём
.
Разобьём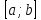 наn
частей, т.е.
наn
частей, т.е.
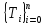 :
:
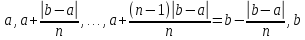 ,
где
,
где
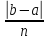 - длина приращения при равномерном
распределении. Поместим область,
ограниченную
- длина приращения при равномерном
распределении. Поместим область,
ограниченную и осью абсцисс в прямоугольник со
сторонами
и осью абсцисс в прямоугольник со
сторонами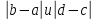 ,
гдеd
и c
– точки на оси ординат, причём
,
гдеd
и c
– точки на оси ординат, причём
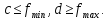 Разобьём
Разобьём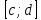 наk
частей, т.е.
наk
частей, т.е.
 :
:
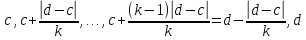 ,
где
,
где
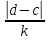 - длина приращения при равномерном
распределении. При данных разбиениях
- длина приращения при равномерном
распределении. При данных разбиениях и
и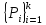 получили (n+1)(k+1)
точек. Рассмотрим способ нахождения
площади под графиком функции
получили (n+1)(k+1)
точек. Рассмотрим способ нахождения
площади под графиком функции
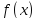 при данном распределении точек. Так как
эта площадь есть какая-то часть площади
прямоугольника, то скажем, что эта часть
есть вероятность попадания этих точек
в саму область под графиком функции
при данном распределении точек. Так как
эта площадь есть какая-то часть площади
прямоугольника, то скажем, что эта часть
есть вероятность попадания этих точек
в саму область под графиком функции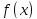 и на её границу. Пусть попавших точек
будетm,
где
и на её границу. Пусть попавших точек
будетm,
где
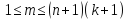 ,
тогда
,
тогда
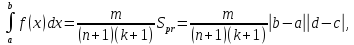
где
 - площадь прямоугольника.
- площадь прямоугольника.
Пример: численно вычислить интеграл
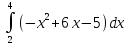
Решение
Сначала вычислим интеграл с помощью формулы Ньютона-Лейбница.
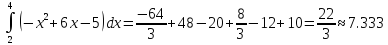
Пусть n=3, k=2, c=0, d=4, то
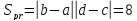 –площадь
выбранного прямоугольника,
–площадь
выбранного прямоугольника,
(n+1)(k+1) = 12 – общее количество точек,
Разбиение
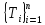 :
2,
:
2,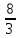 ,
,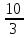 ,
4, разбиение
,
4, разбиение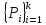 :
0, 2, 4, тогда получаем точки
:
0, 2, 4, тогда получаем точки
(2,0),
(2,2), (2,4), (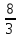 ,0),
(
,0),
(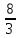 ,2),
(
,2),
(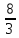 ,4),
(
,4),
(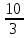 ,0),
(
,0),
(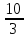 ,2),
(
,2),
(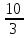 ,4),
(
,4),
(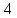 ,0),
(
,0),
(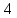 ,2),
(
,2),
(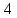 ,4),
из них попадают в область (2,0), (2,2), (
,4),
из них попадают в область (2,0), (2,2), (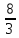 ,0),
(
,0),
(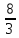 ,2),
(
,2),
(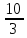 ,0),
(
,0),
(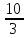 ,2),
(
,2),
(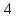 ,0),
(
,0),
(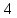 ,2)
– 8 точек, тогда
,2)
– 8 точек, тогда
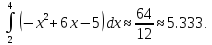
Из
полученного результата мы видим
достаточно большую погрешность,
погрешность до
 достигается при достаточно большом
количестве точек, например 9000, гдеn=100,
k=900.
Это показывает, что данный метод не
очень удобен из-за достаточно медленной
сходимости.
достигается при достаточно большом
количестве точек, например 9000, гдеn=100,
k=900.
Это показывает, что данный метод не
очень удобен из-за достаточно медленной
сходимости.
