
- •МАТЕМАТИКА
- •Кемерово 2012
- •Выбор номеров задач контрольной работы
- •МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ
- •4. Обыкновенные дифференциальные уравнения
- •Таблица 1
- •Дифференциальные уравнения первого порядка
- •Таблица 3
- •Общее решение однородного уравнения
- •Таблица 4
- •Частное решение неоднородного уравнения
- •Обыкновенные дифференциальные уравнения
- •Список рекомендуемой литературы
- •Составители:
- •МАТЕМАТИКА
- •Печатается в авторской редакции
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
« Кузбасский государственный технический университет имени Т. Ф. Горбачева»
Кафедра математики
МАТЕМАТИКА
Контрольная работа № 2 и методические указания для студентов 1 курса (2 семестр)
специальности 130400 «Горное дело», специализаций 130401, 130403, 130404, 130406, 130409 заочной формы обучения
Составители А. И. Бабин Е. А. Волкова Е. В. Прейс
Утверждены на заседании кафедры Протокол № 7 от 08. 02. 2012 г. Рекомендованы к печати учебно–методической комиссией по направлению подготовки специалистов 130400 «Горное дело»
Протокол № от . |
. 2012 г. |
Электронная копия находится в библиотеке КузГТУ
Кемерово 2012
1
Контрольная работа № 2 составлена в соответствии с программой курса «Математика» для студентов специальности 130400 «Горное дело» заочной формы обучения.
В составлении работы и методических указаний к ней принимали участие преподаватели: В. М. Волков, В. А. Гоголин, И. А. Ермакова.
Номера задач контрольной работы студент должен выбрать по таблице «Выбор номеров контрольных задач» следующим образом:
найти строку, соответствующую первой букве фамилии;
найти столбец, соответствующий последней цифре шифра;
на пересечении найденных строки и столбца взять номера задач контрольной работы № 2.
Контрольная работа, выполненная не по своему варианту, возвращается непроверенной.
ПРОГРАММА 1 КУРСА (2 СЕМЕСТР )
Рабочая программа дисциплины «Математика» составлена в соответствии с ФГОС ВПО и примерной ООП подготовки бакалавров специальности 130400 «Горное дело», специализаций
130401, 130403, 130404, 130406, 130409 заочной формы обучения
1. Неопределённый интеграл
1.1.Первообразная (неопределённый интеграл), её свойства. Таблица интегралов.
1.2.Непосредственное интегрирование. Интегрирование по частям и подстановкой.
1.3.Использование таблиц (справочников) неопределённых интегралов.
2.Определённый интеграл
2.1.Задачи, приводящиеся к понятию определённого
интеграла.
2.2.Определённый интеграл как предел интегральных сумм.
2.3.Основные свойства определённого интеграла.
2.4.Производная интеграла по переменному верхнему пределу. Формула Ньютона-Лейбница.

2
Выбор номеров задач контрольной работы
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
А,В,Д |
1 37 |
2 38 76 |
3 39 77 |
4 40 78 |
5 41 79 |
6 42 80 |
7 43 81 |
8 44 82 |
9 45 83 98 |
10 46 84 |
|
75 120 |
91 122 |
92 123 |
93 124 |
94 125 |
95 126 |
96 127 |
97 128 |
129 |
99 130 |
|
121 |
12 48 |
|
|
|
|
|
|
|
|
Б,Е,З |
11 47 |
13 49 |
14 50 |
15 51 |
16 52 |
17 53 |
18 54 |
19 55 |
20 56 |
|
|
85 100 |
86 101 |
87 102 |
88 103 |
89 104 |
90 105 |
91 106 |
92 107 |
93 108 139 |
64 109 |
|
131 |
132 |
133 |
134 |
135 |
136 |
137 |
138 |
|
140 |
Г,Ж, |
21 57 65 |
22 58 66 |
23 59 67 |
24 30 68 |
25 31 69 |
26 32 70 |
27 33 71 |
28 34 72 |
29 35 73 |
30 36 74 |
И,Л |
110 |
111 |
112 |
113 |
114 |
115 |
116 |
117 |
118 |
119 |
К |
1 38 |
2 39 76 |
3 40 77 |
4 41 78 |
5 42 79 |
6 43 80 |
7 44 81 |
8 45 82 |
9 46 83 98 |
10 47 84 |
|
75 120 |
91 142 |
92 143 |
93 144 |
94 145 |
95 146 |
96 147 |
97 148 |
149 |
99 150 |
|
141 |
12 48 |
|
|
|
|
|
|
|
|
М,Н,О |
11 49 |
13 50 |
14 51 |
15 52 |
16 53 |
17 54 |
18 55 |
19 56 |
20 57 |
|
|
85 100 |
86 101 |
87 102 |
88 103 |
89 104 |
90 105 |
61 106 |
62 107 |
63 108 128 |
64 109 |
|
151 |
121 |
122 |
123 |
124 |
125 |
126 |
127 |
|
129 |
П,Х,Ц, |
21 58 65 |
22 59 66 |
23 60 67 |
24 60 68 |
25 39 69 |
26 31 70 |
27 32 71 |
28 33 72 |
29 34 73 |
30 35 74 |
Ш |
110 |
117 |
112 |
113 |
114 |
115 |
116 |
117 |
118 |
119 |
С,У,Ё, |
1 36 75 |
2 37 76 |
3 38 77 |
4 40 78 |
5 41 79 |
6 42 80 |
7 43 81 |
8 44 |
9 45 83 98 |
10 46 84 |
Ы,Й |
91 130 |
92 131 |
93 132 |
94 133 |
95 134 |
96 135 |
97 136 |
82 120 |
138 |
99 139 |
|
|
22 58 |
|
|
|
|
|
137 |
|
|
Р,Т,Ф |
21 57 |
23 59 |
24 60 |
25 36 |
26 31 |
27 32 |
28 33 |
29 34 |
30 35 |
|
|
65 110 |
66 111 |
67 112 |
68 113 |
69 114 |
70 115 |
71 116 |
72 117 |
73 118 148 |
74 119 |
|
140 |
141 |
142 |
143 |
144 |
145 |
146 |
147 |
|
149 |
Ч,Щ,Э |
11 47 |
12 48 |
13 49 |
14 50 |
15 51 |
16 52 |
17 53 |
18 54 |
19 55 |
20 56 |
,Ю,Я |
85 100 |
86 101 |
87 102 |
88 103 |
89 104 |
90 105 |
61 106 |
62 107 |
63 108 128 |
64 109 |
|
150 |
121 |
122 |
123 |
124 |
125 |
126 |
127 |
|
129 |

3
3.Теория функций комплексного переменного
3.1.Комплексные числа и действия над ними.
3.2.Алгебраические действия над комплексными числами.
4.Обыкновенные дифференциальные уравнения
4.1.Задачи, приводящиеся к дифференциальным уравнениям. Основные определения.
4.2.Дифференциальные уравнения первого порядка. Задача Коши. Теорема существования и единственности решения задачи Коши.
4.3.Интегрирование простейших типов дифференциальных уравнений: с разделяющимися переменными, однородных и линейных.
4.4.Дифференциальные уравнения второго порядка. Задача Коши. Уравнения, допускающие понижение порядка.
4.5.Линейные дифференциальные уравнения с постоянными коэффициентами.
4.6.Применение дифференциальных уравнений для решения задач физики и механики.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ
Для вычисления неопределённых интегралов (№ 1-30) необходимо проработать литературу: [2, гл.I, §1 - §7, с. 8-54; 4, п. 6, с. 148 - 168], где содержатся практические рекомендации по данной теме.
Для выполнения задания 1-30 (пункт а) нужно из таблицы интегралов выбрать такой, к которому можно свести данный интеграл.
Например, при вычислении
|
|
dx |
|
= ∫(5x + 2) |
− |
5 |
|
|
∫ 3 |
( |
5 |
3dx |
|||||
5x + 2 |
|
|||||||
|
) |
|
|
|
|
|||
используем табличный интеграл

4
un+1
∫undu = n + 1 + c .
Согласно этой формулы подводим под знак дифференциала
основание степени. Так как |
|
d(5x + 2)= 5dx , то |
умножим и |
||||||||||||||||||||||||||
разделим интеграл на 5, то есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
dx |
|
|
|
|
− |
5 |
|
|
1 |
|
|
− |
5 |
|
|
|
1 |
|
|
− |
5 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
∫ |
3 |
( |
5x + 2 5 |
= ∫(5x + 2) |
|
3dx = |
5 ∫(5x |
+ 2) |
|
|
3 5dx = 5 |
∫(5x + 2) |
|
3d(5x + 2)= |
|||||||||||||||
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
− |
5 |
+1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
1 |
(5x + 2) 3 |
+ c = − |
3 |
(5x + 2)− |
+ c = − |
|
|
3 |
|
+ c . |
||||||||||||||||||
3 |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
5 |
− |
5 |
+ |
1 |
|
|
10 |
|
|
|
|
|
|
|
|
103 |
( |
5x |
+ 2 2 |
|
|
|
|
|||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Интеграл |
∫x e3x 2 −1dx |
сводится |
|
к |
табличному |
∫eudu = eu + c |
|||||||||||||||||||||
путём подведения под знак дифференциала показателя степени d(3x2 − 1)= 6xdx. Таким образом
|
2 |
|
|
1 |
2 |
|
|
|
1 |
|
2 |
−1d(3x |
2 − 1) |
1 |
|
2 |
|
|
|
|
||
∫x e3x |
|
−1dx = 6 ∫e3x |
|
−1 |
6xdx = |
6 |
∫e3x |
|
= 6 e3x |
|
|
−1 + c . |
||||||||||
В примере |
∫ |
3cosx dx |
используем формулу |
∫ du |
= ln |
|
u |
|
+ c , где |
|||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
2 + sinx |
|
|
|
|
|
|
|
|
|
u |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
под знаком дифференциала находится знаменатель дроби. Так
как d(2 + sinx)= cosxdx , то
3∫ |
cosxdx |
= 3∫ |
d(2 + sinx) |
= 3 ln |
|
2 + sinx |
|
+ c. |
|
|
|
||||||||
2 + sinx |
2 + sinx |
||||||||
|
|
|
|
|
|
|
При вычислении интегралов в пункте б) применяются методы подстановки и интегрирования по частям, то есть по формуле
∫udv = uv − ∫ vdu мы от исходного интеграла |
∫udv переходим к |
|||||||
более простому ∫ vdu . |
|
|
|
|
|
|
|
|
Пример. ∫x arctgxdx = ∫arctgx xdx , то есть возьмём |
||||||||
|
|
|
dx |
|
|
|
|
|
u = arctgx du = |
|
|
|
, |
|
|
|
|
|
+ x |
2 |
|
|
||||
|
1 |
|
|
|
|
|
||
|
|
|
|
|
|
2 |
||
|
|
|
|
|
|
x |
|
|
dv |
= xdx v = ∫dv |
= ∫xdx = |
|
. |
||||
|
|
|||||||
|
|
|
|
2 |
|
|||

5
(здесь при нахождении v константу c полагаем равной 0). Получим
|
|
|
|
|
∫x arctgxdx = ∫arctgx |
xdx = |
x2 |
|
arctgx − |
1 |
∫x2 |
|
|
|
|
dx |
|
. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
2 |
1 + x2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Возьмём |
|
∫x2 |
|
|
|
|
отдельно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
+ x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
∫x2 |
|
|
dx |
|
|
|
+ 1 |
− 1 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
= x − arctgx + c |
||||||||||||||||||||||
|
|
|
|
|
|
= |
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
dx = |
∫ |
− |
|
|
|
|
|
dx = ∫dx − ∫ |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
1 |
+ x2 |
|
|
x2 + |
1 |
|
|
|
|
|
|
1 |
+ x2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Итак |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
∫x arctgxdx = |
arctgx − |
1 |
(x − arctgx)+ c . |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример. Найти |
∫x e−3xdx . Пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
u = x du = dx, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
−3x |
|
|
|
|
|
|
|
|
|
|
−3x |
|
|
|
|
|
1 |
|
|
|
|
−3x |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
−3x |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d(− 3x)= − |
|
|
. |
|||||||||||||||||||||||||||||||||||
|
|
|
|
dv = e |
|
|
|
|
|
dx v = ∫e |
|
|
|
|
dx |
= − |
|
|
|
∫e |
|
|
|
|
|
e |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
−3x |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
−3x |
|
|
|
|
|
|
1 |
|
|
|
|
−3x |
|
|
|
|
|
|
|
|
|
xe |
−3x |
|
|
1 |
|
|
|
−3x |
|
|
|
|
|
|
|||||||||||||||
∫x e |
|
|
dx = x |
− |
|
|
|
e |
|
|
− ∫ |
− |
|
|
|
e |
|
|
|
dx = − |
|
|
|
|
|
+ |
|
|
|
∫e |
|
|
dx = |
|
|||||||||||||||||||||||||||||||||
|
|
3 |
|
|
|
3 |
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
xe−3x |
|
e−3x |
+ c . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= − |
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
3 |
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Пример. При вычислении интеграла I = ∫ |
|
2 + |
|
|
x + 1 dx сделаем |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x + 3 |
|
|
|
|
|
|
|||||
подстановку u = |
|
|
x + 1 u2 = x + 1 x = u2 − 1 dx = 2udu, |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x + 3 = u2 − 1 + 3 = u2 + 2 . Получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2u + u2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
I = ∫ |
2 + |
x + 1 dx = |
∫ |
|
|
|
2 + u 2udu = 2∫ |
du . |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2u + u2 |
|
|
|
|
|
|
x + 3 |
|
|
|
|
|
|
|
|
|
u2 + 2 |
|
|
|
|
|
|
|
|
|
u2 + 2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Дробь |
|
|
|
|
неправильная |
(степень |
числителя |
|
не |
меньше |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
u2 + 2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
степени знаменателя). Выделим целую часть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(u2 + 2)− 2 + 2u |
= 1 − |
|
2 |
|
|
+ |
|
|
|
2u |
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u2 + 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
u |
2 u2 + 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
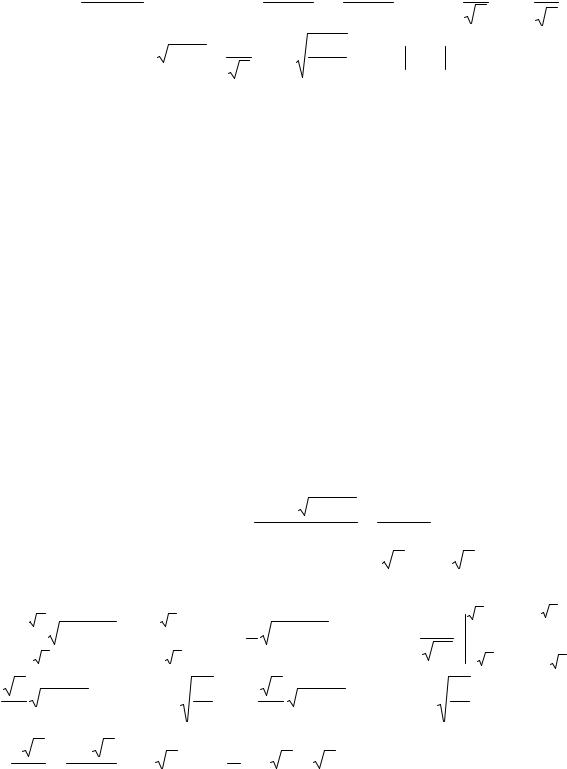
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
Итак |
I = |
2∫ |
2u + u2 |
|
|
|
∫du − |
∫ |
2du |
+ ∫ |
2udu |
− |
4 |
arctg |
u |
+ |
||||
u2 + 2 |
du = 2 |
u2 + |
= 2u |
2 |
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
u2 + 2 |
|
|
|
|||||||
+ 2 ln(u2 + 2)+ c = 2 x + 1 − 4 |
arctg |
x + 1 + 2 ln x + 3 + c. |
|
|
|
|||||||||||||||
|
|
|
|
du |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
Здесь ∫du и ∫ |
|
|
табличные, а |
|
|
|
|
|
|
|
||||||||||
u2 + |
2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
d(u2 + 2) |
|
|
|
|
|
|
|
||||||
|
|
|
|
∫ |
2udu |
= ∫ |
= ln(u2 + 2)+ c . |
|
|
|
|
|
||||||||
|
|
|
|
u2 + 2 |
|
u2 + 2 |
|
|
|
|
|
|
||||||||
Для нахождения площадей плоских фигур и объёмов тел вращения в задачах № 31-60 рекомендуется изучить литературу
[2, гл. II, § 2, с. 67 - 68; 4, п. 7.11 – 7.12, с. 185-190].
Пример. Найти площади частей, на которые круг x2 + y2 = 12 делится параболой y = x2 .
Сделаем схематический чертёж (рис.1) и найдём точки пересечения этих линий
|
|
|
|
|
|
2 |
+ y |
2 |
= 12 |
|
|
|
|
2 |
= 12 − y |
2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
x |
|
|
|
|
|
x |
|
|
12 |
− y2 = y |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
= x |
|
|
|
|
|
|
= y |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
y |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
y2 + y − 12 = 0 y = − 1 ± 1 + 48 = − 1 ± 7 |
, y = 3. |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
В |
|
точке |
|
пересечения |
|
|
x2 = 3 x1 = − |
3, x2 = |
|
|
3 . |
Площадь |
||||||||||||||||
меньшей части |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
S1 = |
3 |
12 |
− x2 dx − |
3 |
x2dx = |
x |
12 |
− x |
2 + 6 arcsin |
x |
|
|
3 |
|
x3 |
|
3 |
|||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
− |
|
= |
|||||||||||||||||||||||||||
∫ |
∫ |
|
2 |
12 |
|
|
3 |
|
||||||||||||||||||||||
|
|
− |
3 |
|
|
|
|
|
|
− |
3 |
|
|
|
|
|
|
|
|
|
− |
3 |
|
− 3 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= |
|
3 |
12 − 3 + 6 arcsin |
3 |
|
|
− |
3 |
12 |
− 3 − 6 arcsin |
|
3 |
|
− |
|
|
|
|||||||||||||
|
2 |
12 |
− |
2 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
||||||
− |
|
3 |
3 |
− |
− |
3 3 |
|
= 3 3 |
+ 12 |
π |
− 2 3 = 3 + 2π. |
|
|
|
|
|
|
|
|
|
||||||||||
|
3 |
|
|
|
|
3 |
|
|
6 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
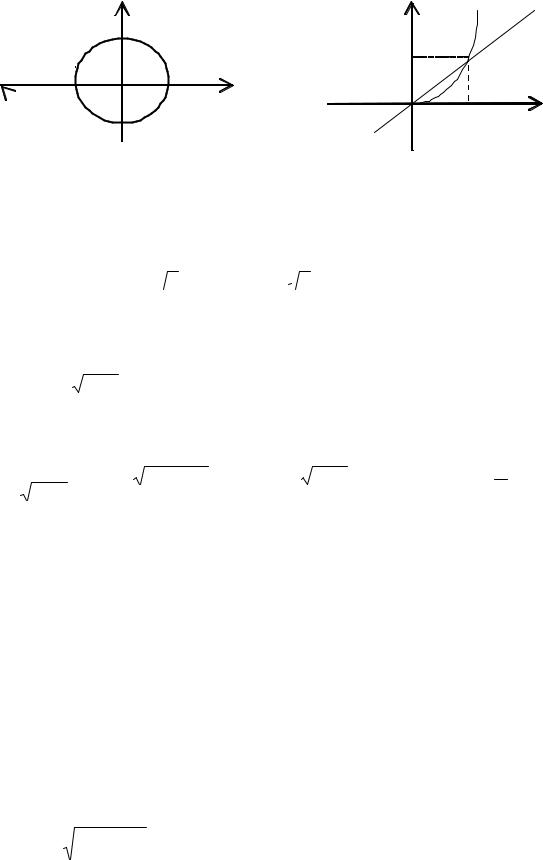
7
y
 y =x2 y
y =x2 y
y = x
x
x
x2 + y2 = 12
Рис.1 |
Рис.2 |
Площадь большей части
S2 = πr2 − S1 = π 12 −  3 − 2π = 10π −
3 − 2π = 10π −  3 .
3 .
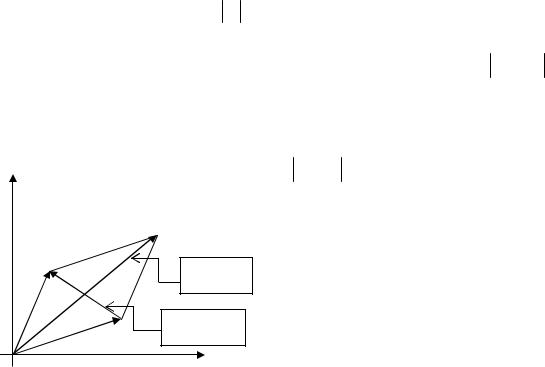
Пример. Найти объём тела, образованного вращением
вокруг |
оси |
OX |
|
|
фигуры, |
|
ограниченной |
линиями |
||||||
y = x, |
y = x |
sinx, |
0 ≤ x ≤ π . |
|
|
|
|
|
|
|
||||
Сделаем схематический чертёж (рис.2) и найдём точки |
||||||||||||||
пересечения этих линий |
|
|
|
|
|
|
|
|
|
|||||
y = x |
x − x |
sinx = 0, x1 = 0, 1 − |
|
sinx |
= 0, sinx = 1, x2 |
= π . |
||||||||
|
|
|||||||||||||
y = x |
sinx |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
π |
|
|
π |
|
|
V = V |
|
− V |
b |
2dx |
b |
|
|
2 |
|
|
2 |
|
|
|
|
= π∫ y |
− π∫ y2dx = |
π∫x2dx − π∫x2 sinxdx = |
||||||||||
|
1 |
2 |
1 |
|
a |
2 |
|
0 |
|
|
0 |
|
||
|
|
|
|
a |
|
|
|
|
|
|
|
|||
|
|
3 |
|
|
|
|
|
|
π |
|
|
3 |
|
|
|
|
− 2xsinx + |
( |
x2 |
− 2 |
|
2 |
|
π |
|
|
|||
|
= π x |
|
cosx |
|
= π |
|
− π + 2 , |
|
||||||
|
3 |
|
|
|
) |
|
0 |
|
24 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫x2 sinxdx = 2xsinx −(x2 − 2)cosx. |
|
|
|
|
|||||||||
При нахождении длины дуги в задачах № 31-60 и массы неоднородной линии в задачах № 61-90 следует помнить, что дифференциал длины дуги выражается различными формулами
[2, гл. II, § 2.2, с. 68; 4, п. 7.10.11, с. 184 - 185].
1) ds = 1 + (y′x )2 dx , если линия задана в декартовых координатах;
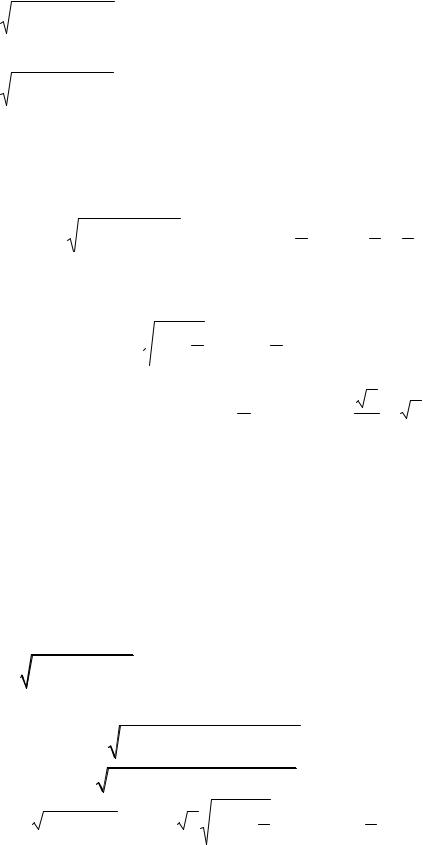
8
|
2) ds = |
|
(x′t )2 + (y′t )2 dt , |
если |
линия |
|
задана |
параметрически |
|||||||||||||||||
|
x = x(t), y = y(t); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
3) ds = |
|
r2 + (r′(θ))2 dθ, |
|
если |
линия |
|
|
задана |
|
в |
|
полярных |
||||||||||||
|
координатах r = r(θ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример. Найти длину дуги кривой r = cos2 θ |
, |
0 ≤ θ ≤ |
π . |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ |
2 |
|
|
θ |
|
1 |
2 |
|
|
Вычисляем |
|
ds = |
r2 + (r′(θ)) |
2 |
dθ, rθ′ = 2cos |
|
|
|
. |
|
|
||||||||||||||
|
|
2 |
− sin |
2 |
|
2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
r2 |
+ (r′(θ)) |
2 |
= cos4 |
θ |
+ cos2 |
θ |
sin2 |
θ |
= cos2 |
θ |
|
|
|
θ |
+ sin2 |
θ |
θ |
, |
|||||||
|
|
2 |
2 |
2 |
2 |
cos2 |
2 |
|
= cos2 |
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||
ds =  cos2 θ2dθ = cos θ2 dθ,
cos2 θ2dθ = cos θ2 dθ,
ππ
2 |
θ |
dθ = 2sin |
θ |
|
2 |
|
π |
|
= 2 |
2 |
= |
2 . |
|
||||||||||||
S = ∫cos |
|
|
|
|
= 2 sin |
|
− sin0 |
|
||||
0 |
2 |
|
2 |
|
0 |
|
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
Пример. Найти массу участка линии
x = a(t −sint),
L : 0 ≤ t ≤ 2π, если плотность γ = 3y .
y = a(1 −cost),
|
|
|
|
|
|
m = ∫γ ds . |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
||
Найдём ds = |
(x′t )2 + (y′t )2 dt , |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
x′t |
= a(1 − cos t), y′t = a sin t , |
|
|
|
|
||||||||
|
|
|
ds = |
a2 (1 − cost)2 + a2 sin2 t dt = |
|
|
|
|
||||||||
|
|
|
= a |
1 − 2cost + cos2 t + sin2 t dt = |
|
|
|
|
||||||||
|
|
= a |
2 − 2cost dt = a 2 |
2sin2 t |
dt = 2a sin t |
dt . |
|
|
||||||||
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|||
|
2π |
|
|
|
t |
|
2π |
t |
|
t |
|
|
2π |
t |
|
|
m = |
∫ 3a(1 |
− cost) 2a sin |
dt = 6a2 |
∫ 2sin2 |
sin |
dt = 12a2 |
∫ sin3 |
dt = |
||||||||
|
2 |
|
2 |
|||||||||||||
|
0 |
|
|
2 |
|
0 |
2 |
|
|
0 |
|
|||||
9
= 12a2 |
|
− 2cos |
t |
+ |
1 |
2 cos3 |
t |
|
|
2π |
= 12a |
2 |
|
2 |
− |
2 |
+ 2 − |
2 |
= 32a2 . |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
3 |
|
|
|
|
3 |
|
|||||||||||||
|
|
|
|
|
2 |
|
0 |
|
|
|
|
|
|
3 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.Теория функций комплексного переменного
3.1.Комплексные числа и действия над ними.
Более подробный теоретический материал и практические рекомендации по данной теме ( № 61-90) можно найти, например,
в следующих учебниках: [1, т. 1, гл. VI, § 1, 2, с. 134 - 137; 3, т.2, § 5.3, с. 239-244].
Комплексными числами называются числа вида z = x + i y , где i2 = -1, x, y – действительные числа, x = Re z – действительная часть, y = Im z – мнимая часть комплексного числа.
По определению, |
два |
комплексных |
числа: |
z1 = x1 + i y1 |
и |
|
z2 = x2 + i y2 – равны тогда и только тогда, когда и y1 = y2 . |
|
|||||
Комплексное число |
z |
называется |
сопряженным |
|||
комплексному числу |
z , если Re z = Re z, |
Im z = -Im z . Другими |
||||
словами, если z = x + i y , то |
z = x − i y . |
|
|
|
||
Всякому комплексному |
числу |
x + i y |
можно поставить |
в |
||
соответствие единственную точку плоскости M(x, y) и обратно,
всякую точку M(x, y) плоскости XOY |
можно рассматривать |
как геометрический образ единственного |
комплексного числа |
x + i y . |
|

10
y |
Для сокращения |
вместо “точка, |
|
соответствующая |
комплексному |
Мчислу x + i y ”, говорят просто “точка
|
x + i y ”. |
При |
этом множество всех |
|
|
действительных чисел изображается |
|||
0 |
х точками |
оси абсцисс, |
которая |
|
Рисунок 1 |
поэтому |
называется действительной |
||
|
осью, множество чисто мнимых |
|||
|
чисел |
i y |
точками оси |
ординат, |
|
называемой |
мнимой |
осью. |
|
|
Заметим, что одна точка мнимой |
|||
|
оси, а именно начало координат, |
|||
изображает действительное число нуль. Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью.
Внекоторых случаях удобно считать геометрическим
изображением числа
JJJJG
O M {x, y}.
y
0 z3
5 x
 -2 z2
-2 z2
 -5 z1
-5 z1
Рисунок 2
x + i y радиус-вектор точки M(x, y) –
Пример 1. Построить точки
z1 = 5 − 5i , z2 = −2i , z3 = 5 .
В дальнейшем, наряду с представлением комплексных чисел в декартовых координатах, полезно иметь их представление в обобщенных полярных координатах.
Рассмотрим число
которому |
на плоскости |
соответствует |
точка M(x, y) . |
Ее координаты в полярной системе координат (ρ, ϕ).

11
y |
Тогда |
x = ρ cos ϕ, |
||||||
M(x; y) |
|
y = ρ sin ϕ. |
||||||
|
|
|
|
|
|
|
||
ρ |
z = x + i y =ρ cos ϕ+ i ρ sin ϕ = |
|||||||
φ |
= ρ(cos ϕ+ i sin ϕ). |
|||||||
|
Полярный радиус |
|||||||
0 |
x |
|||||||
JJJG |
называется модулем |
|||||||
Рисунок 3 |
ρ = |
OM |
||||||
|
комплексного числа и |
|||||||
|
обозначается |
|
z |
|
= ρ. |
|||
|
|
|
||||||
Полярный угол |
ϕ называется |
аргументом комплексного |
||||||
числа и обозначается |
ϕ = Arg z . Тогда |
|
|
|
|
|
|
|
z = ρ(cos ϕ+ i sin ϕ)= z (cos Arg z + i sin Arg z).
Эта форма называется тригонометрической формой
комплексного числа.
Модуль комплексного числа определяется однозначно: z = x2 + y2 .
Аргумент комплексного числа определяется с точностью до
слагаемого, кратного |
2π. Главным |
значением |
аргумента |
называется значение, заключенное в |
интервале |
(−π, π]. |
|
Обозначается оно arg z . Таким образом, |
−π < arg z ≤ π. |
|
|
Очевидно, Arg z = arg z + 2k π.
Главное значение аргумента определяется однозначно.
Так как tg arg z = y , |
|
|
||
|
|
x |
|
(x, y) I, IV четвертям, |
|
y |
, |
если |
|
arctg x |
||||
|
y |
|
|
(x, y) II четверти, |
|
+ π, |
если |
||
arg z = arctg |
x |
|||
|
|
|
(x, y) III четверти. |
|
|
y |
− π, |
если |
|
arctg |
x |
|||
|
|
|
|
|
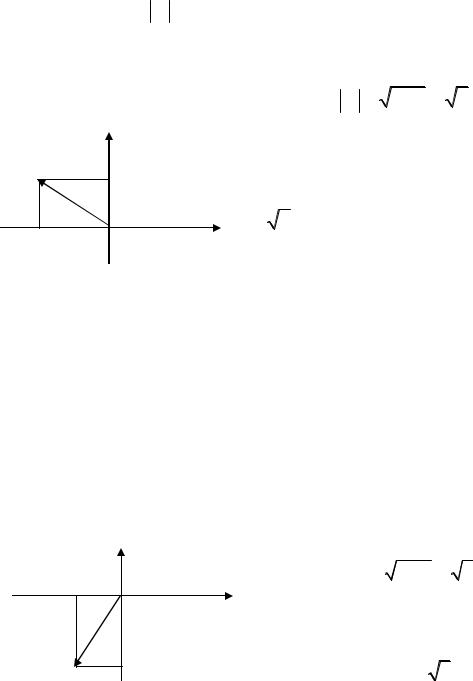
Тригонометрическая форма комплексного числа будет иметь вид
12
z = z (cos(arg z + 2k π)+ i sin(arg z + 2k π)).
Пример 2.
комплексное число
y
z 1
-1
x
Написать в тригонометрической форме z =1 + i .
Решение. z = 1 +1 = 2, tg ϕ = −1,
arg z = arctg(−1)+ π = − π4 + π = 43 π.
z = |
2 |
|
3 |
|
3 |
|
||
cos |
4 |
π + 2k π |
+ i sin |
4 |
π + 2k π . |
|||
0 |
|
|
|
|
|
|
||
Рисунок 4 |
|
|
|
|
|||||||
Пусть |
z = x + i y = |
|
z |
|
(cos Arg z + i sin Arg z). Используя формулу |
||||||
|
|
||||||||||
Эйлера |
cos ϕ + i sin ϕ = ei ϕ , |
|
получаем |
так |
называемую |
||||||
показательную форму записи комплексного числа: |
|
||||||||||
|
|
|
|
|
z = |
|
z |
|
ei Arg z . |
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 3. Представить в показательной форме комплексное
число z = −1 − i . |
Решение |
|
|
|
|
|
|
||||
|
y |
|
|
|
|
|
|
||||
-1 |
0 |
|
z |
|
= 1 +1 = |
2, |
tg ϕ=1, |
||||
|
|
||||||||||
|
|
|
|
π |
|
|
|
3 |
|
||
|
x |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
arg z = |
4 |
− π = − 4 π, |
||||
z |
-1 |
|
|
|
−1 − i = |
2 e |
− |
3 |
πi+2k πi |
. |
|
|
|
|
|
||||||||
|
|
|
4 |
|
|||||||
Рисунок 5
Пример 4. Вычислить eπi .
Решение. По формуле Эйлера eπi = cos π + i sin π = −1 .
13
3.2. Алгебраические действия над комплексными числами.
Для выполнения алгебраических действий над комплексными числами (№ 91-120) необходимо проработать литературу: [1, т. 1, гл. VI, § 3, с. 137, 138; 3, т.2, § 5.3, с. 239-244],
где содержатся теоретический материал и практические рекомендации по данной теме.
Сложение и умножение комплексных чисел производится по правилам сложения и умножения алгебраических многочленов с учетом i i = −1. При записи результата следует отделить действительную часть от мнимой, т. е. собрать отдельно члены, содержащие множитель i , и члены, не содержащие множитель i :
(x1 + i y1 )+ (x2 + i y2 )= (x1 + x2 )+ i(y1 + y2 ),
(x1 + i y1 ) (x2 + i y2 )= (x1 x2 − y1 y2 )+ i(x1 y2 + y1 x2 ),
(x1 + i y1 )−(x2 + i y2 )= (x1 − x2 )+ i(y1 − y2 ).
В частности, z z = z 2 . Операции сложения и вычитания
сводятся к сложению и вычитанию векторов, изображающих эти числа. Отсюда расстояние между точками ρ(z1, z2 )= z1 − z2 .
y
z1
z1+z2
z2
z1–z2
0 |
x |
Рисунок 6
Пример 5.
z − z0 = R – уравнение окружности с центром в точке
z0
и радиусом равным R .
Деление на комплексное число, отличное от нуля, определяется как действие, обратное умножению.

14
Для представления частного в виде Re z + i Im z
следует провести простые преобразования, показанные на следующем примере.
Пример 6. |
3 − i |
|
(3 − i)(1 − 2i) |
3 − 6i − i − 2 |
|
1 |
− 7i 1 |
|
7 |
||
|
= |
|
= |
1 + 4 |
= |
|
5 |
= 5 |
− |
5 i . |
|
1 + 2i |
(1 + 2i)(1 − 2i) |
|
|||||||||
Для модуля и аргумента произведения и частного справедливы следующие утверждения:
1. z1 z2 = z1 z2 , Arg z1 z2 = Arg z1 + Arg z2 .
Пример 7. Найти модуль и аргумент произведения z i .
Решение. |
|
z i |
|
= |
|
z |
|
π |
|
|
|
|
|
|
|||||||
|
|
|
|
, Arg z i = Arg z + |
2 |
+ 2k π . |
||||
|
|
|
|
|
|
|
|
|
|
|
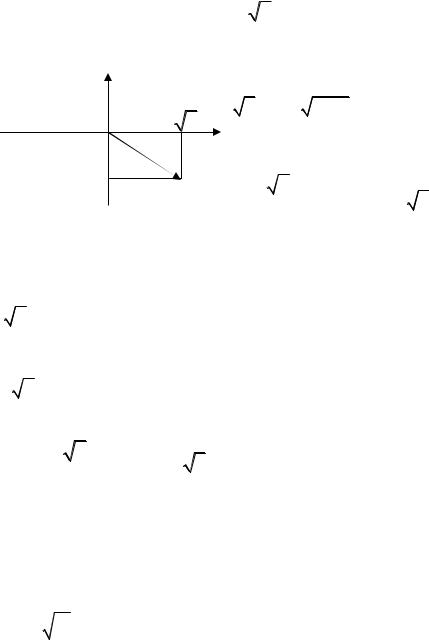
Таким образом, умножение на i соответствует повороту вектора z на угол;
2. |
|
z1 |
|
= |
|
|
z1 |
|
|
|
, |
Arg |
z1 |
= Arg z1 − Arg z2 . |
|
|
|
||||||||||||
z2 |
|
|
z2 |
|
|
z2 |
||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Пусть z = z (cos Arg z + i sin Arg z).
Тогда z2 = z z = z 2 (cos2Arg z + i sin2 Arg z).
Можно доказать методом полной математической индукции, что
для любого целого |
n > 0 : zn = |
|
z |
|
n (cos n Arg z + i sin n Arg z) |
|
|
(формула Муавра). Формула справедлива и для целых отрицательных n .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
Пример 8. Вычислить ( 3 − i)5 . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
y |
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
3 − i |
|
= |
3 +1 = 2, |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
x |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
arg( |
|
3 − i)= arctg |
|
− |
|
1 |
|
= − |
π |
, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||||||||||||||
|
|
|
|
|
-1 |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Рисунок 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3 − i = |
2 |
|
|
− |
π |
+ |
|
|
+ i sin |
|
− |
π |
+ 2k |
|
|
|
|
|
|
|
|
|
|
|||||
cos |
6 |
2k π |
|
6 |
π , |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
( 3 − i) |
5 |
= 25 |
|
|
|
− |
5 |
π+ |
|
|
|
|
|
|
|
|
5 |
π+10k |
|
= |
|
|
||||||
|
cos |
6 |
10k π |
+ i sin − |
6 |
π |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3 |
|
1 |
|
= −16 3 −16i . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= 32 − |
|
− i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Корнем n -й степени из комплексного числа называется такое число w , для которого wn = z .
Используя формулу Муавра, получим
|
|
w |
|
= n |
|
z |
|
, |
Arg w = Arg z = arg z + 2k π, k = 0, 1, 2, ... , n −1. |
||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
n |
n |
аргументы будут отличаться от |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Для |
других значений |
k |
|||||
полученных на число кратное |
2π, и, следовательно, получатся |
||||||||||
значения корня, совпадающие с рассмотренными. Итак, корень n -й степени из комплексного числа имеет n различных значений.
