подготовка к Начертательной геометрии

1. Методы проецирования и их свойства. Обратимость чертежа.

Проецирование – это процесс получения изображения чего-либо на что-либо.

1. Под методом проецирования понимается существование плоскостей проекций, объекта проецирования и проецирующих лучей. (Проекцией точки А на плоскости П0 есть точка А0 пересечение проецирующего луча с плоскостью проекций, который проходит через т А):

2. В зависимости от положения центра проецирования относительно плоскости проекций проецирование может быть центральным или параллельны. При центральном проецировании проецирующие лучи выходят с одной точки — центра проецирования S, который находится на определённом расстоянии от плоскости проекций П0. Центральное проецирование обладает наглядностью, оно используется при изображении предметов в перспективе. Основной недостаток — трудность определения размеров по его изображению.

3. При параллельном проецировании, проецирующие лучи проходят параллельно один одному. В этом случае считают, что центр проекций отдален в бесконечность. При параллельном проецировании задается направление проецирования — S и плоскость проекций. В зависимости от направления проецирования относительно плоскости проекций параллельные проекции могут быть прямоугольными, если проецирующие лучи проходят перпендикулярно к плоскости проекций, и косоугольными, если проецирующие лучи не перпендикулярные к плоскости проекций.

Основные свойства прямоугольного параллельного проецирования:

1) проекция точки есть точка;

2) проекция прямой есть прямая;

3) если точка принадлежит прямой, то одноименная проекция точки находится на одноименной проекции прямой;

4) если точка делит отрезок в каком-то соотношении, то проекция отрезка делится в таком же соотношении;

5) если две прямые параллельны между собой, то их одноименные проекции то же параллельны;

6) если две прямые пересекаются между собой, то они имеют общую точку, проекции этих прямых так же имеют общую точку, связанную проекционной связью.

Обратимость чертежа – это его свойство, позволяющее по изображению предмета судить о его форме и размерах.

2. Комплексный чертеж точки в системе двух и трех плоскостей проекций. Построение чертежа точки по ее координатам и определение координат точки по ее чертежу.

Комплексный чертеж - это ортогональное изображение предмета на две или более взаимоперпендикулярные плоскости проекций, совмещенные с плоскостью чертежа.

Комплексный чертеж в системе двух плоскостей проекции имеет две взаимноперпендикулярные плоскости проекции. При проецировании плоскости на чертеж П₂ – (фронтальная плоскость проекции) неподвижна, а П₁ – (горизонтальная плоскость проекции) вращается вокруг оси Ox совмещаясь с плоскостью чертежа. В эпюре из трех плоскостей проекций к двум уже имеющимся проекциям плоскостей добавляется третья плоскость П₃ – (профильная проекция). При построении комплексного чертежа используется метод прямоугольного или ортогонального проецирования.

Алгоритм построения наглядного изображения точки, заданной координатами (рис. 2.30):

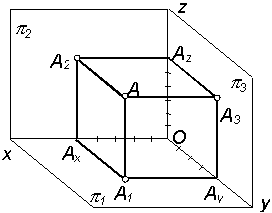
1.1. Соотнести знаки координат x, y, z с данными табл. 2.3.

1.2. Определить четверть, в которой расположена точка.

1.3. Выполнить наглядное (аксонометрическое) изображение четверти.

1.4. Отложить координаты точки на осях А_Х, А_Y, А_Z.

1.5. Построить проекции точки на плоскостях p₁, p₂, p_3.

1.6. Построить перпендикуляры к плоскостям p₁, p₂, p₃ в точках проекции А₁, А₂, А₃.

1.7. Точка пересечения перпендикуляров есть искомая точка А.

2. Алгоритм построения комплексного чертежа точки в системе трех плоскостей проекций p ₁, p ₂, p ₃, заданной координатами (рис. 2.32)

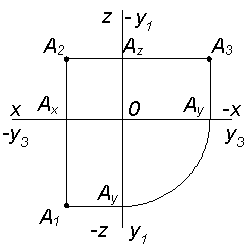
2.1. Определить по координатам четверть, в которой расположена точка.

2.2. Определить механизм совмещения плоскостей.

2.3. Построить комплексный чертеж четверти.

2.4. Отложить координаты точки на осях x, y, z (А_Х, А_Y, А_Z).

2.5. Построить проекции точки на комплексном чертеже.

3. Конкурирующие точки.

Конкурирующие точки – это точки, лежащие на одном проецирующем луче. Фронтально конкурирующие точки, лежат в одной точке на фронтальной плоскости проекции П₂, а горизонтально проецирующие точке лежат в одной точке на горизонтальной плоскости проекции П₁.

4. Комплексный чертеж прямой. Принадлежность точки прямой. Деление отрезка в данном отношении.

Прямая на чертеже может быть задана эпюром двух точек. Точка принадлежит прямой, если проекции принадлежат одной проекции прямой. Ли-ния k₁ и k₂ должна быть вертикальной и перпендикулярной к оси проекции Ox

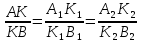Если точка делит отрезок в некотором отношении, то проекция точки делит проекцию отрезка в том же самом отношении.

5. Прямые общего и частного положения. Прямые уровня. Их чертежи и свойства. Проецирующие прямые, их чертежи и свойства.

Прямые по своему положению к проекции делят на: прямые общего положения (произвольно расположенные); прямые частного положения (прямые параллельно или перпендикулярно плоскостям проекции).

• Прямые частного положения их делят на прямые уровня и проецирующие прямые

1. Прямые уровня – это прямые параллельные одной из плоскостей проекции.

1. Горизонталь (h/g) – прямая параллельная горизонтальной плоскости проекции П₁

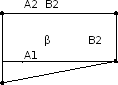
• z – const  h₂ || Ox

• AB Є h  A₁B₁=НВ(AB)

нв

2. Фронталь (f) – прямая параллельная фронтальной плоскости

проекции П₂

• y – const  f₂ || Ox

  нв

• AB Є f  A₂B₂=НВ(AB)

3. Профильная прямая – прямая параллельная профильной проекции П₃

• x – const  A₂B₂ ┴ Ox

AB || П₃ A₁B₁ ┴ Ox

нв

• A₃B₃=НВ(AB)

2. Проецирующие прямые – это прямые перпендикулярные одной из плоскостей проекции

1. Горизонтально проецирующая прямая перпендикулярна П₁

   нв

2. Фронтально проецирующая прямая перпендикулярна П₂

3. Профильно проецирующая прямая перпендикулярна П₃

   нв

   

A₂ B₂ A₃≡B₃

нв

нв

A₁ B₁

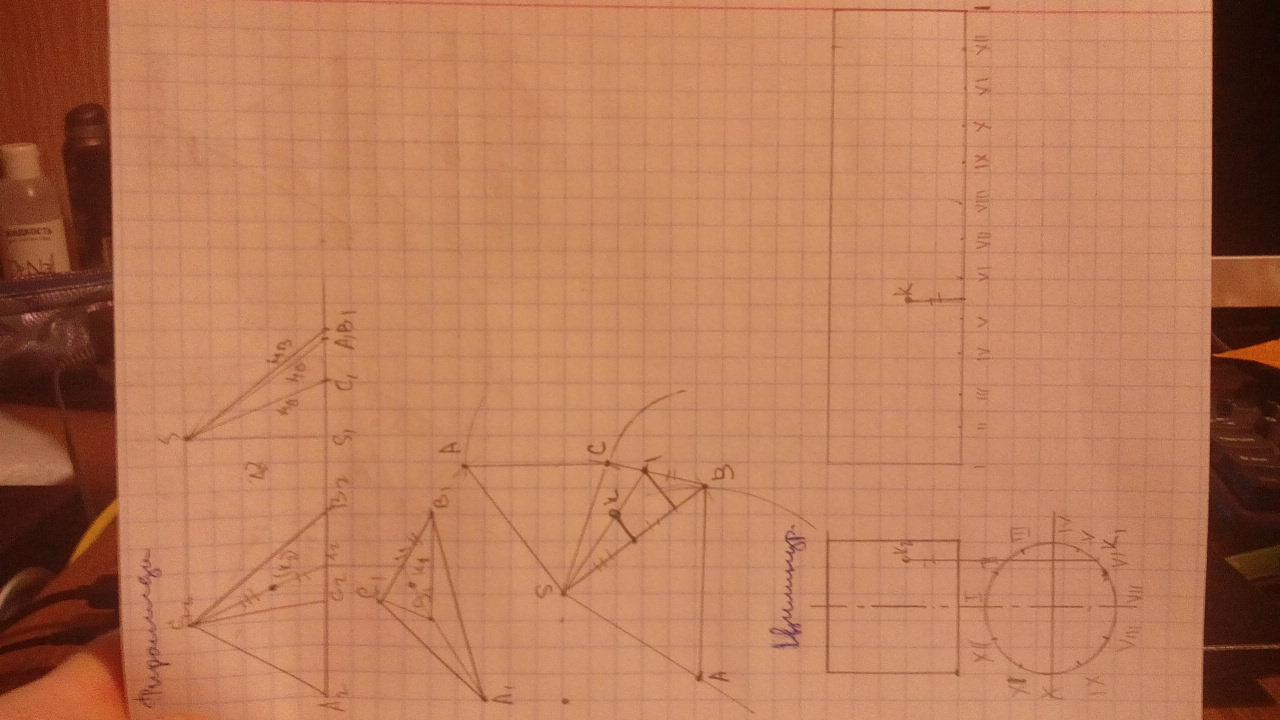
6. Определение натуральной величины отрезка общего положения с помощью прямоугольного треугольника.

Чтобы найти натуральную величину отрезка общего положения надо, на чертеже построить прямоугольный треугольник один катет которого разместить на проекции отрезка, тогда второй катет должен быть равен разнице координат концов отрезка взятой с другой проекции.

7. Взаимное положение прямых и их изображение на чертеже.

Если прямые параллельны между собой, то их одноименные проекции параллельны.

a||ba₁||b₁; a₂||b₂

Прямые пересекаются, если пересекаются их одноименные проекции и точки пересечения, проекции лежат на одной линии связи

mXn = Km₁Xn₁=K₁; m₂Xn₂=K₂; K₁K₂┴x

Скрещивающиеся прямые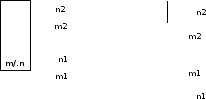

8. Теорема о проецировании прямого угла.

Прямой угол проецируется на плоскость без искажения, если одна из его сторон параллельна этой плоскости (рис. 122).

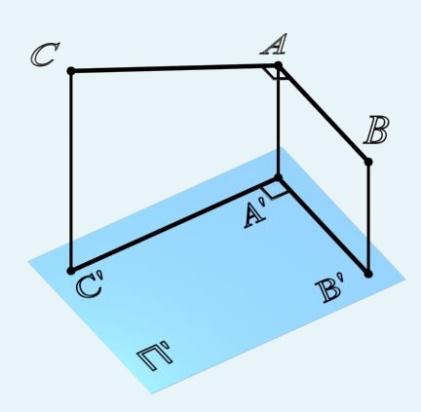
Рис. 122. Теорема о проекциях прямого угла

Дано: ∠BAC = 90º; AB∥ П'

Доказать, что С'A'⊥A'B'

Доказательство: если AB∥ П', то A'B'∥AB, но AA'⊥П' ⇒ AA'⊥A'B' значит AB⊥AA' AB⊥ плоскости , тогда и A'B'⊥CAA'C'. Следовательно, C'A'⊥A'B'.

На основании этой теоремы две взаимно перпендикулярные прямые (пересекающиеся или скрещивающиеся) проецируются на П₁ в виде взаимно перпендикулярных прямых, если одна из них горизонталь, на П₂ – если одна из них фронталь (рис. 123, а).

Условие перпендикулярности скрещивающихся прямых (рис. 123, б) сводятся к условиям перпендикулярности пересекающихся прямых, поведенных через произвольную точку и соответственно параллельных скрещивающимся прямым. Таким образом, понятие перпендикулярности можно отнести как к пересекающимся, так и к скрещивающимся прямым.

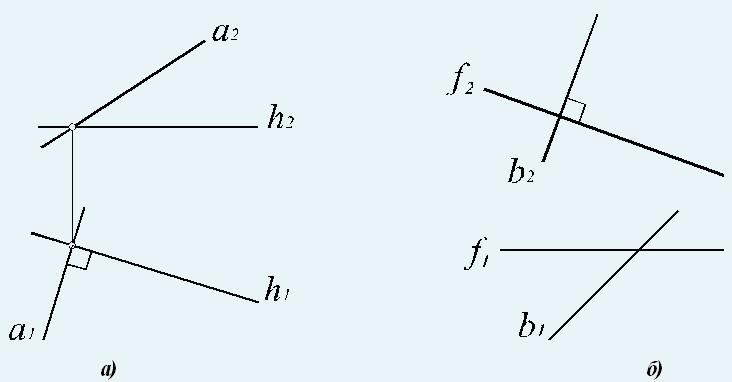
Рис. 123. Перпендикулярные прямые: а - пересекающиеся a₁⊥h₁⇒a⊥h ; б - скрещивающиеся b₂⊥f₂⇒b⊥f ;

9. Задание плоскости на чертеже.

Плоскости на чертеже могут быть заданы одним из следующих способов:

а) Эпюром трех точек не лежащих на одной прямой

б) Прямой и точкой на ней не лежащей

в) Двумя пересекающимися прямыми

г) Двумя параллельными прямыми

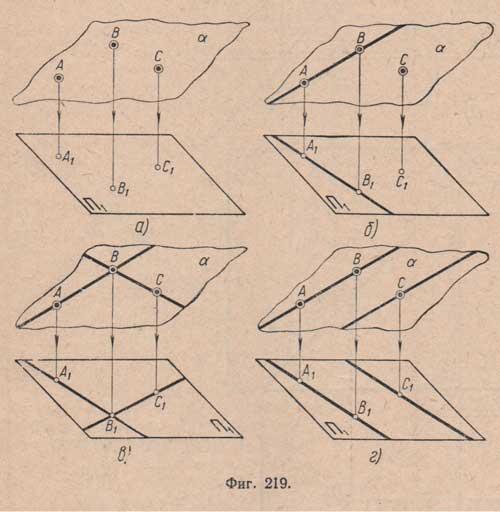
д) любая плоская фигура.

10. Плоскости общего и частного положения. Плоскости частного положения и их свойства.

Плоскости по своему положению по отношению к плоскостям проекции, делят на плоскости общего положения (произвольно расположенные) и частного (параллельные либо перпендикулярно расположенные).

Плоскость частного положения делят на плоскости уровня и проецирующие плоскости:

Плоскость уровня – это плоскости параллельные какой либо плоскости проекции.

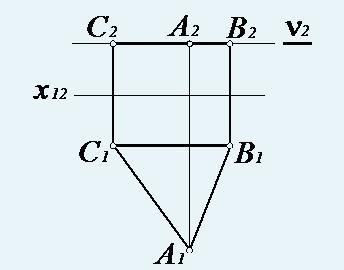
1. Горизонтальная плоскость уровня ГПУ ∥ П₁ – плоскость, параллельная горизонтальной плоскости проекций

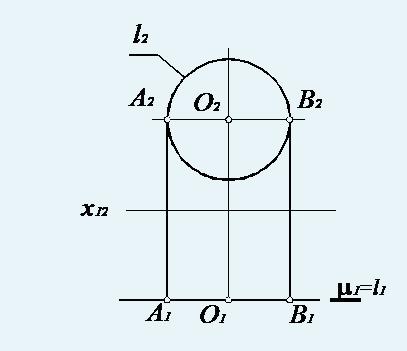
2. Фронтальная плоскость уровня ФПУ ∥ П₂ – плоскость, параллельная фронтальной плоскости проекций

3. Профильная плоскость уровня ППУ ∥ П₃ – плоскость, параллельная профильной плоскости проекций

Проецирующие плоскости – это плоскости перпендикулярные какой либо плоскости проекции

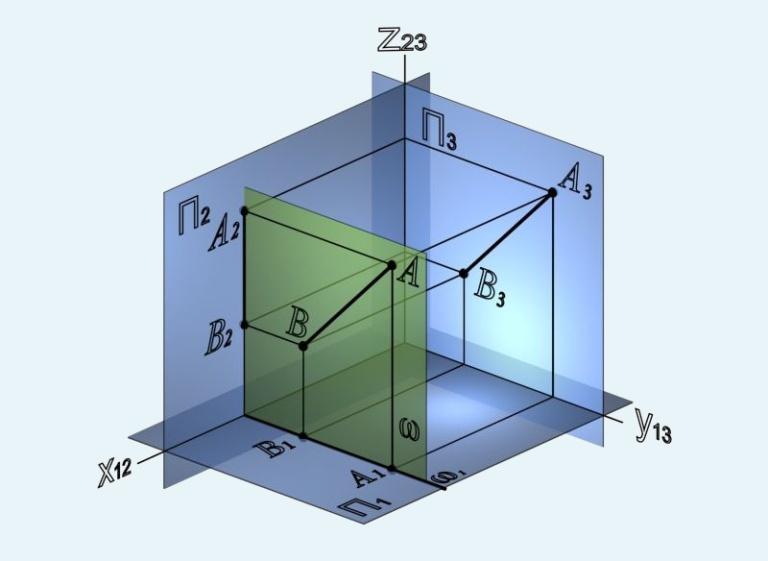
1. Горизонтально-проецирующая плоскость ГПП ⊥ П₁ – плоскость, перпендикулярная горизонтальной плоскости проекций П₁

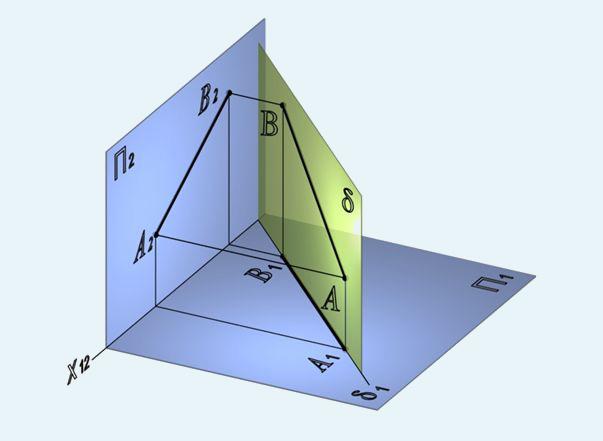
2. Фронтально-проецирующая плоскость ФПП ⊥ П₂ – плоскость, перпендикулярная фронтальной плоскости проекций П₂

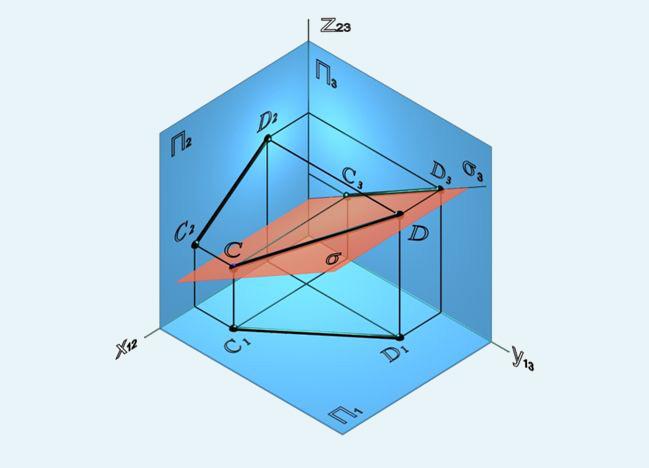
3. Профильно-проецирующая плоскость ППП ⊥ П₃ – плоскость, перпендикулярная профильной плоскости проекций П₃

11. Принадлежность прямой плоскости. Главные линии плоскости.

Прямая принадлежит плоскости если пересекает две прямые образующие плоскость.

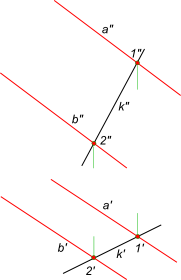
Эта задача регистрирует условия что прямая принадлежит плоскости, кроме этого она регистрирует принадлежность точки плоскости.

12. Принадлежность точки плоскости.

Точка плоскости принадлежит, если через нее можно провести прямую лежащую в плоскости.

13. Параллельность прямой и плоскости. Параллельность плоскостей.

Прямая плоскости параллельна, если она параллельна хотябы одной прямой лежащей в плоскости.

Плоскости параллельны, если две пересекающиеся прямые параллельны двум пересекающимся прямым другой плоскости.

14. Построение линии пересечения двух плоскостей, одна из которых проецирующая.

Линией пересечения двух плоскостей является прямая, для построения которой достаточно определить две точки, принадлежащие обеим плоскостям одновременно.

.

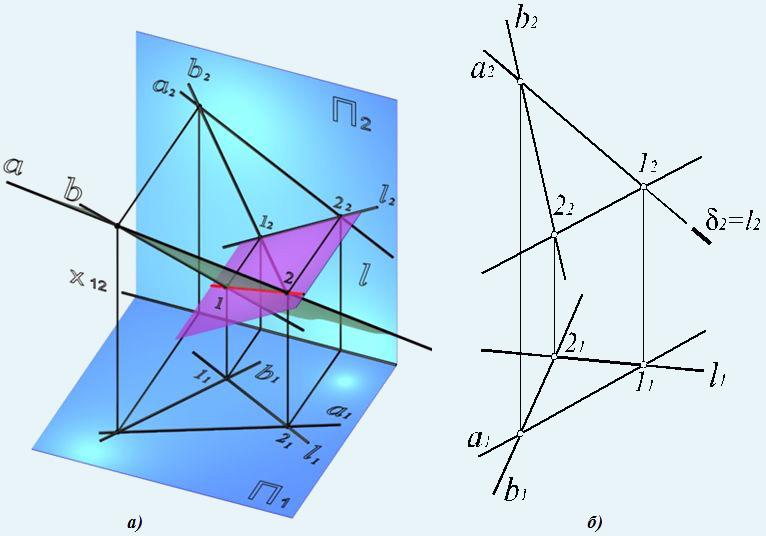
Рис. 75. Пересечение плоскости общего положения с проецирующей плоскостью а – наглядное изображение; б – комплексный чертеж

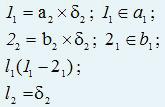
Рассмотрим построение линии пересечения l плоскости общего положения α(a×b) и фронтально-проецирующей плоскости δ(δ2) (рис. 75, б). Линия, по которой пересекаются две плоскости, принадлежит обеим плоскостям одновременно, следовательно, для ее построения достаточно определить две точки, общие для пересекающихся плоскостей, или одну точку и направление линии пересечения. В данном случае, достаточно определить точки пересечения прямых a и b с плоскостью δ(δ2). Они однозначно определят линию пересечения l.

15. Пересечение прямой с плоскостью. Частные случаи пересечения прямой с плоскостью.

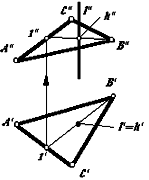
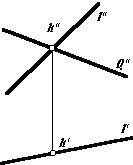
Пересечение проецирующей прямой с плоскостью (рис. 4.2,а) определяется из условия принадлежности точки пересечения заданной плоскости (см. тему 3).  Пересечение прямой с проецирующей  плоскостью (рис. 4.2,а) определяется в пересечении вырожденной проекции плоскости и соответствующей проекции прямой.

На рис. 4.2,б  задана фронтально проецирующая плоскость, пересечение  вырожденной  проекция  которой с проекций прямой l'' на эту же плоскость определяет точку пересечения. Как видим, решение позиционных задач при таком расположении простые. 

16. Основная позиционная задача по определению точки пересечения прямой с плоскостью.

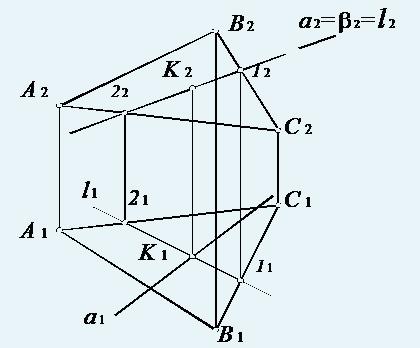
Задача об определении точки пересечения прямой общего положения с плоскостью общего положения называется первой позиционной задачей. На рис. 76 представлено наглядное изображение решения первой позиционной задачи.

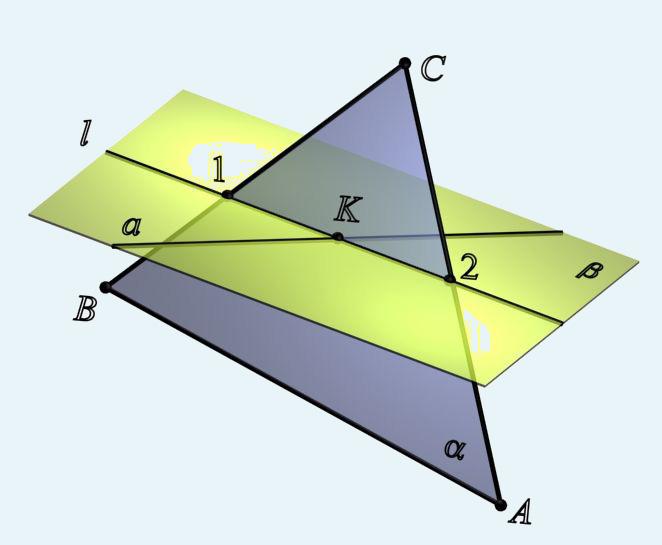
Для того чтобы найти точку пересечения прямой с плоскостью нуно:

1. через прямую провести проецирующую плоскость;

2. построить линию пересечения заданной плоскости с проецирующей;

3. точка пересечения построенная линией с заданной прямой и есть точка пересечения прямой с плоскостью.

Видимость прямой a по отношению к плоскости на фронтальной плоскости проекций (рис. 79) определяется с помощью конкурирующих точек 2 – на прямой (AC) и 3 – на прямой a. Глубина точки 3 больше, следовательно, видима будет прямая a.

17. Перпендикулярность прямой и плоскости.

Прямая плоскости перпендикулярна, если она перпендикулярна горизонтали и фронтали плоскости.

Взаимно перпендикулярные прямая и плоскость могут быть построены на эпюре Монжа из условия перпендикулярности прямой к двум пересекающимся прямым, принадлежащим этой плоскости.

Если в плоскости взять пересекающиеся горизонталь и фронталь, то появляется возможность воспользоваться теоремой о проецировании прямого угла.

Построение прямой перпендикулярной к плоскости общего положения заданной треугольником.

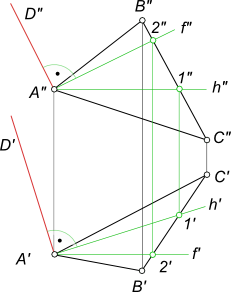
18. Методы преобразования проекций. Метод замены плоскостей проекций.

1. Вращение точки вокруг проецирующей прямой;

2. Вращение вокруг линии уровня;

3. Плоскопараллельное перемещение

Все вышеперечисленные методы предусматривают вращение или перемещение геометрических элементов при неподвижных плоскостях проекции.

Метод замены плоскостей проекции. Этот метод позволяет при неизменном положении геометрических элементов в пространстве подбирать плоскости проекции так, чтобы геометрические элементы по отношению к новым плоскостям проекции заняли бы частное положение.

19. Решение метрических задач заменой плоскостей проекций.

Все метрические задачи можно разбить на две группы:

1. Задачи связанные с прямыми:

1. Задача: Определить расстояние от точки до прямой

2. Задача: Определить расстояние между двумя прямыми

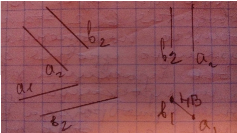
3. Задача: Определить расстояние между скрещивающимися прямыми

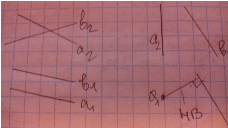
4. Здача: Определить НВ двухгранного угла

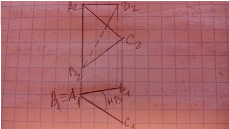
Эти задачи объединены частными случаями, в которых одна или обе прямые являются проецирующими. По этому для того чтобы их решить нужно преобразовать прямую общего положения в проецирующую прямую. Это преобразование проводится в два этапа:

1. Прямую общего положения преобразуем в прямую уровня, для этого новую ось проекции x’ выбираем параллельно одной из проекций прямой;

2. Прямую уровня преобразуем в проецирующую прямую, для этого ось x” выбираем перпендикулярно прямой, построенной на первом этапе.

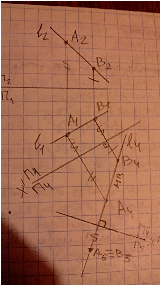
2. Задачи связанные с плоскостями:

1. Определить расстояние от точки до плоскости;

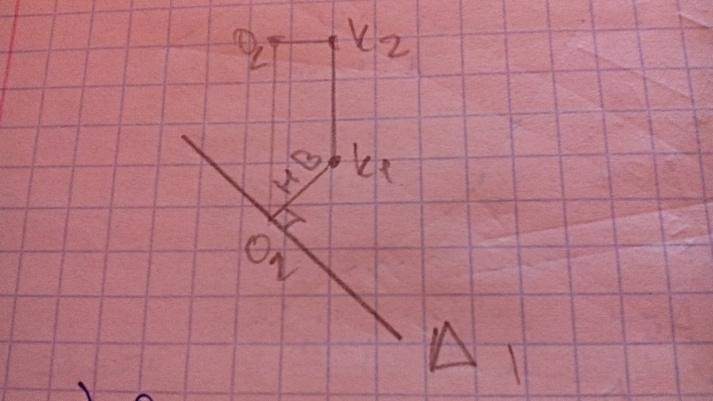
2. Определить расстояние между параллельными плоскостями

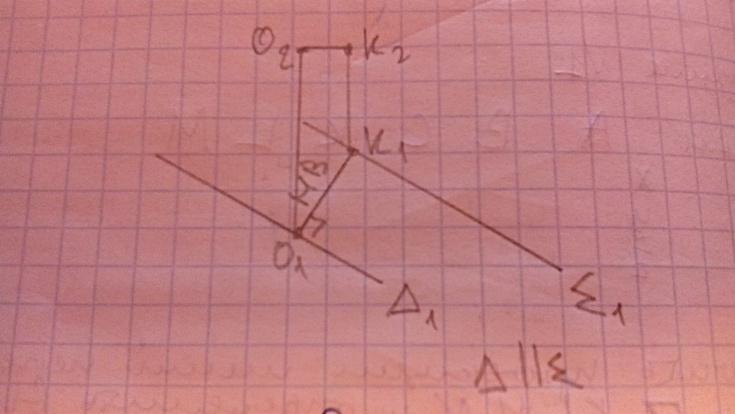
3. Проведение всевохможных построений в плоскости

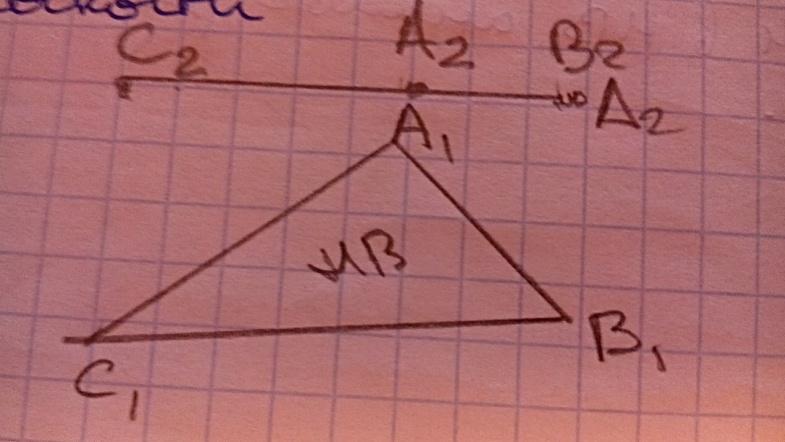
Все эти задачи объединены частными случаями, которых плоскость является проецирующей плоскостью следовательно, если дана плоскость общего положения, ее можно преобразовать в проецирующую и решать задачу в частном виде.

Преобразования плоскости общего положения в проецирующую проводятся:

1. Плоскость общего положения преобразуем в плоскость проецирующую, для этого ось x’ выбираем либо перпендикулярно h₁ либо перпендикулярно f₂. В этом случае можно решить первые две задачи;

2. Продолжив преобразование проецирующей плоскости в плоскость уровня, выбираем x” параллельно прямой в которую спроецировалась плоскость в первом преобразовании. В результате на плоскость П₅ плоскость спроецируется в НВ и тогда можно решать все задачи связанные с построением.

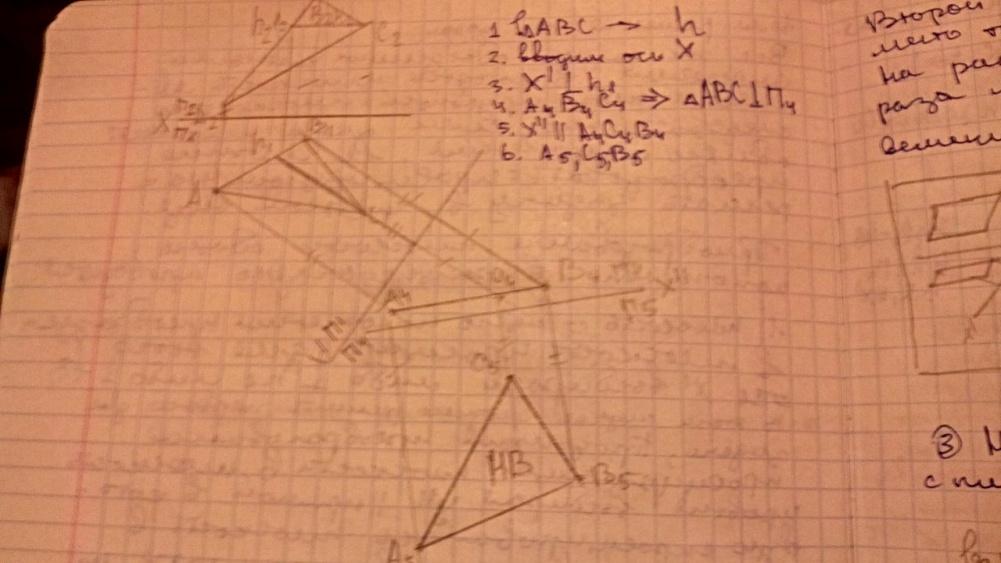
20. Поверхности. Принадлежность точки поверхности.

Существует множество поверхностей, рассматривать будем поверхности вращения и многогранники.

Поверхности вращения: Цилиндр, конус, шар, тор.

Поверхности многогранники: Куб, пирамида, призмы и т.д.

Точка на поверхности. Точка принадлежит поверхности, если через нее можно провести линию лежащую на поверхности.

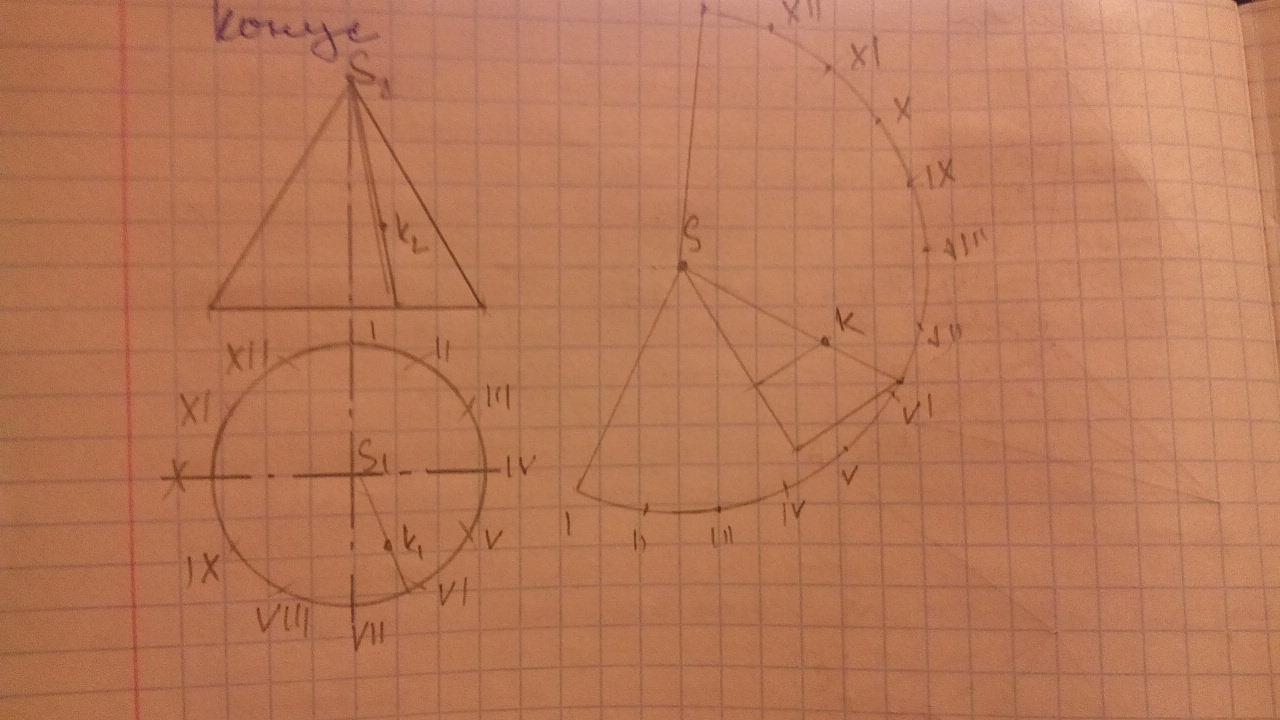
21. Сечение поверхностей проецирующими плоскостями.

Если плоскость пересекает поверхность, то образуется линия пересечения, все точки этой линии принадлежат одновременно и плоскости, и поверхности. Исходя из того, что секущая плоскость является проецирующей, одна проекция линии пересечения является прямой лежащей на проекции плоскости в пределах поверхности. Вторую проекцию линии пересечения строят из условия принадлежности точек этой линии поверхности.

22. Пересечение прямой с поверхностью. Определение точек пересечения прямой с поверхностью.

Чтобы определить взаимное положение прямой и поверхности нужно:

1. Через прямую провести проецирующую плоскость;

2. Построить линию пересечения поверхности с этой плоскостью.

3. Проанализировать полученные данные:

1. Если построенная линия не имеет с заданной прямой ни одной общей точки, то эта прямая с поверхностью не имеет ни одной общей точки;

2. Если построенная линия и заданная прямая имеют одну общую точку, то эта прямая касается поверхности в этой точке;

3. Если построенная линия и заданная прямая имеют две общие точки, то эта прямая пересекает поверхность в этих точках.

23. Взаимное пересечение поверхностей. Основные методы построения линии пересечения поверхностей.

Пересекаясь поверхности образуют линию пересечения все точки которой принадлежат обеим поверхностям.

Форма линии пересечения может быть различной, она зависит от того какие поверхности пересекаются между собой.

1. Если пересекаются 2 многогранника, то линия пересечения есть ломанный пространственный многоугольник;

2. Если пересекаются поверхность вращения и многогранник, то линия пересечения является пространственная кривая, состоящая из плоских веток;

3. Если пересекаются поверхности вращения, то линия пересечения есть пространственная кривая.

Любая задача по пересечению поверхностей начинается с анализа исходных данных:

Если одна из поверхностей проецируется в линию это означает, что одна проекция линии пересечения известна, она лежит на линии, в которую спроецировалась поверхность в пределах очерка второй поверхности. В этом случае вторую проекцию линии пересечения ищут из условия принадлежности точек линии второй поверхности; во всех остальных случаях применяют специальные методы построения линии пересечения с поверхностью:

1. Метод вспомогательных секущих плоскостей;

2. Метод вспомогательных секущих концентрических сфер;

3. Метод вспомогательных эксцентрических сфер.

24. Развертка поверхностей