Расчетно-графическая по теории вероятностей

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА 4(2)

для студентов 221, 222, 223, 225 групп

Теория вероятностей и математическая статистика

Задание 1. Выберите задачу Вашего варианта и решите (5 баллов).

1. Вероятность того, что деталь, изготовляемая на первом станке, будет первосортной, равна 0,7. При изготовлении детали на втором станке эта вероятность равна 0,8. Изготовлено пять деталей. Две из них изготовлены на первом станке. Какова вероятность того, что все детали первосортные?

2. В мешочке имеются карточки с буквами П, Р, О, С, Т, О. Какова вероятность, вынимая случайным образом буквы одну за другой, получить слово “СПОРТ”?

3. В цехе пять моторов. Вероятность того, что мотор включен, равна 0,9. Какова вероятность того, что включены три мотора?

4. Окрашенный деревянный куб распилен так, что каждое его ребро разделено на 8 равных частей. Полученные кубики ссыпаны в урну. Какова вероятность вынуть из урны случайным образом кубик, у которого ровно две грани окрашены?

5. В урне находятся карточки с буквами С, Т, Р, Е, К, О, З, А. Какова вероятность получить слово “КОЗА”, вынимая четыре буквы последовательно одна за другой случайным образом?

6. Какова вероятность того, что при последовательном вынимании четырех букв из урны с буквами А, Р, И, Ф, М, Е, Т, И, К, А, получим слово “ИКРА”?

7. Деревянный куб, три грани которого окрашены, распилен на 1000 кубиков одинакового размера. Полученные кубики ссыпаны в урну и перемешаны. Какова вероятность вынуть кубик с одной окрашенной гранью? (Рассмотреть два случая окраски граней большого куба).

8. Вероятность хотя бы одного попадания при трех выстрелах равна 0,936. Какова вероятность поражения мишени при двух выстрелах?

9. Деревянный куб, пять граней которого окрашены, распилен так, что каждое ребро разделилось на 9 равных частей. Полученные кубики ссыпаны в урну и перемешаны. Какова вероятность вынуть кубик с двумя окрашенными гранями?

10. Какова вероятность, вынимая по одной три карточки последовательно из набора карточек с буквами В, О, З, Д, У, Х, получить слово “УХО”?

11. В мешочке имеются карточки с буквами П, Р, О, С, Т, О, Т, А. Какова вероятность, выбирая случайным образом пять букв по одной, получить слово “СПОРТ”?

12. Десять учебников, среди которых три книги по теории вероятностей, нужно расставить на полке. Какова вероятность того, что при случайной расстановке книг учебники по теории вероятностей будут стоять рядом?

13. Какова вероятность того, что при случайной расстановке букв А, А, М, М, Г, И, К, А, Р, Т в ряд получится слово “ГРАММАТИКА”?

14. В ящике находятся буквы З, А, К, О, Н. Какова вероятность, вынув последовательно четыре буквы, получить слово “КОЗА”?

15. В ящике находятся 13 стандартных и пять бракованных деталей. Какова вероятность того, что среди пяти взятых деталей окажутся две бракованные?

16. Какова вероятность того, что при случайной расстановке букв К, О, М, Б, И, Н, А, Т получится слово “КОМБИНАТ”?

17. Измерено 100 шариков. Результат измерения – нормальная случайная величина со средним 10 мм и дисперсией 4 мм². Диаметр шарика оценивается как среднее арифметическое полученных измерений. Какую точность измерения можно гарантировать с вероятностью 0,997?

18. В лотерее используется 1000 билетов, из которых 300 выигрышных. Найти вероятность выигрыша хотя бы по одному билету, если куплено 10 билетов. Сколько билетов нужно купить, чтобы можно было рассчитывать на выигрыш с вероятностью не меньшей, чем 0,6?

19. Деревянный куб, у которого окрашены две смежные грани, распилен так, что каждое ребро разделено на 10 равных частей. Полученные кубики ссыпаны в урну и перемешаны. Какова вероятность вынуть убик с одной окрашенной гранью?

20. Вероятность того, что событие появится хотя бы один раз в двух испытаниях, равна 0,75. Найти вероятность того, что при четырех испытаниях событие появится три раза.

21. В партии из 40 изделий 10 бракованных. Случайным образом отобрано 4 изделия. Какова вероятность того, что они все без брака?

22. В мастерской 12 измерительных приборов, из которых 6 проходили настройку. Настройщик наугад берет 2 прибора. Какова вероятность того, что они все проходили настройку?

23. На полке 26 книг, из которых 17 на русском языке. Наугад взяли 3 книги. Какова вероятность того, что они все на русском языке?

24. В аквариуме плавают 24 рыбки, из которых половину составляют гуппи. Кот случайным образом поймал 4 рыбки. Какова вероятность того, что ему достались только гуппи?

25. Область лежит внутри круга радиуса R=3. Вычислить вероятность попадания случайной точки в область

D=

26. На складе находятся 6 костюмов 48 размера, 10 костюмов 50 размера и 5 костюмов52 размера. Случайным образом выбирают 2 костюма. Найти вероятность того, что они окажутся одного размера.

27.Пусть (а; в) – координаты случайной точки в квадрате К=(а;в)а1,в1. Найти вероятность того, что корни уравнения х²+х+ав=0 действительны.

28.На отрезке прямой ОА поставлены случайным образом две точки В и С. Найти вероятность того, что длина ВС будет меньше длины ОВ. Предполагается, что вероятность попадания точки на отрезок не зависит от расположения этого отрезка, а зависит только от его длины.

29.Какова вероятность попадания случайной точки в область

целиком лежащую внутри круга, заданного неравенством х²+у²1?

30.Вероятность попадания точки М(х; у) в область Д, лежащую целиком внутри круга К=(х; у)х²+у²1, пропорциональна площади этой области Д. Вычислить вероятность попадания случайной точки в область

Д=(х; у)х²+у²1, х²2у.

Задание 2. Выберите задачу Вашего варианта и решите (7 баллов).

1. На каждые 20 пластинок, изготовленных на станке, приходится в среднем три бракованных. Определить вероятность того, что из 700 взятых наугад изделий 600 будут бездефектными.

2. Вероятность того, что деталь стандартна, равна 0,9. Сколько деталей нужно обобрать, чтобы с вероятностью 0,9544 можно было утверждать, что относительная частота появлений нестандартных деталей (среди отобранных) отклонится от вероятности по абсолютной величине не более, чем на =0,03?

3. Какова вероятность того, что сумма двух чисел, взятых из промежутка (0; 1), будет не больше единицы, а произведение не больше 2/9?

4. Составьте ряд распределения числа попаданий по кольцу баскетболистом при трех бросаниях мяча, если вероятность попадания при одном бросании 0,6. Вычислить математическое ожидание числа попаданий.

5. Вероятность хотя бы одного попадания при двух выстрелах 0,96. Составить ряд распределения числа попаданий при четырех выстрелах.

6. Вероятность хотя бы одного попадания при трех выстрелах равна 0,973. Какова дисперсия при десяти выстрелах?

7. Вероятность хотя бы одного попадания при трех выстрелах равна 0,875. Какова вероятность поражения мишени при четырех выстрелах?

8. В первой урне 5 белых шаров и 7 красных. Во второй урне 6 белых шаров и 8 красных. Из каждой урны вынули по одному шару и положили с третью урну. Какова вероятность вынуть белый шар из третьей урны?

9. При автоматической штамповке деталей наблюдается 10% брака. Какова вероятность, что в партии из 1000 изделий отклонение от от указанного процента будет менее 0,028?

10. При автоматической штамповке деталей наблюдается 10% брака. Какова вероятность, что в партии из 1000 изделий отклонение от от указанного процента будет менее 0,028?

11. Станок – автомат дает в среднем 90% изделий первого сорта. Найти вероятность того, что среди трехсот изделий число изделий первого сорта будет от 264 до 279.

12. В круг вписан правильный треугольник. Какова вероятность того, что брошенные в круг две случайные точки попали внутрь треугольника?

13. Вероятность появления события в одном испытании равна 0,6. Найти вероятность того, что при 1200 независимых испытаниях отклонение частоты от вероятности по абсолютной величине не превысит 0,05.

14. Два студента обусловили место встречи в течении часа. Пришедший первым ждет другого 15 мин. Какова вероятность, что встреча состоится?

15. На контроль поступают одинаковые блюда, изготовленные двумя поварами. Производительность первого повара вдвое больше, чем второго. Процент брака у первого повара 0,8%, у второго – 0,6%. Проверяемое блюдо не удовлетворяет требованиям контроля. Найти вероятность того, что оно изготовлено вторым поваром.

16. Для некоторой местности число дождливых дней в августе равно 11. Чему равна вероятность того, что первые три дня августа будут дождливыми.

17. Первый магазин выполняет план с вероятностью 0,9, а второй – с вероятностью 0,6, а третий – с вероятностью 0,7.Найти вероятность того, что план выполнят не менее двух магазинов.

18. Три автомата изготовляют одинаковые детали. Их производительности относятся как 2:3:5, а стандартные детали среди их продукции составляют в среднем соответственно 96%, 97%, 99%. Найти вероятность того, что наугад взятая деталь стандартная.

19. 60% шерстяной пряжи окрашивается в яркие тона. Какова вероятность того, что среди пятисот мотков пряжи, поступивших в торговлю, число мотков яркой окраски окажется от 280 до 320?

20. Вероятность хотя бы одного попадания при трех выстрелах равна 0,875. Какова вероятность двух попаданий при четырех выстрелах?

21. Пассажир обращается с вероятностью 0,7 в одну кассу и с вероятностью 0,3 – в другую. Вероятность приобрести требуемый билет в первой кассе равна 0,6, а во второй – Найти вероятность того, что пассажир купил билет.

22. Три спортсмена участвуют в отборочных соревнованиях. Вероятности зачисления в сборную команду первого, второго и третьего спортсменов соответственно равны 0,8, 0,7, 0,6. Найти вероятность того, что хотя бы один из них попадет в сборную.

23. Человек, заблудившийся в лесу, вышел на пересечение трех тропинок. Вероятность выхода из леса в течение оставшегося дня составляет соответственно 0,8, 0,4, 0,6 для каждой тропинки. Чему равна вероятность того, что человек вышел из леса в этот день, если он выбирает одну из трех тропинок с равной вероятностью?

24. Имеется коробка с девятью новыми теннисными мячами. Для игры берут три мяча, после игры их кладут обратно. При выборе мячей игранные мячи от новых не отличают. Какова вероятность того, что после трех игр в коробке не останется новых мячей?

25. Во время испытаний было установлено, что вероятность безотказного срабатывания реле при отсутствии помех равна 0,99., при перегреве – 0,95, при вибрации – 0,9, при вибрации и перегреве – 0,8.Найти вероятность отказа этого реле при работе в жарких странах, где вероятность перегрева равна 0,2, вероятность вибрации – 0,1, перегрев и вибрация – независимые события.

26. В пункте проката имеется 10 телевизоров, для которых вероятность исправной работы в течение года равна 0,9 и 5 телевизоров с вероятностью исправной работы 0,95. Найти вероятность того, что наугад взятый телевизор будет работать исправно в течение года.

27. Монета подбрасывается до тех пор, пока впервые не появится герб. Какова вероятность того, что будет произведено не более трех бросаний монеты?

28. Вероятность опечатки на странице рукописи равна 0,3. В рукописи 210 страниц машинописного текста. Найти вероятность того, что в рукописи не более 50 страниц с опечатками.

29. В шкафу находятся 8 однотипных приборов. В начале опыта все приборы новые. Для временной эксплуатации берут наугад 2 прибора, после эксплуатации их возвращают в шкаф. Найти вероятность того, что после четырехкратного выбора и эксплуатации не останется новых приборов.

30. В отделение связи поступило 4 телеграммы. Всего имеется 4 канала связи. Телеграммы случайным образом распределяются по каналам. Каждая телеграмма с одной и той же вероятностью передается по любому из четырех каналов. Найти вероятность того, что все четыре телеграммы будут переданы по одному каналу.

Задание 3. Выберите задачу Вашего варианта и решите (8 баллов).

1. Составьте ряд распределения числа попаданий, если при одном выстреле вероятность попадания в мишень р=0,8, а произведено пять выстрелов. Приведите график функции распределения.

2. У человека в кармане 4 ключа, из которых только один подходит к двери его квартиры. Ключи последовательно извлекаются (без возвращения) до тех пор, пока не появится нужный ключ. Найти закон распределения случайной величины ξ – числа ключей, вынутых из кармана. Найти математическое ожидание и дисперсию. Составить функцию распределения, построить ее график.

3. Вероятность появления события в одном испытании р=0,4. Найти число испытаний n, при котором с вероятность. 0,7698 можно ожидать, что относительная частота появления отклонится от его вероятности по абсолютной величине не более, чем на =0,02.

4. Случайное отклонение размера детали от заданного – нормальная случайная величина с параметрами а=0, =8. Годными считаются те детали, для которых отклонение заключено в пределах 110 см. Найти среднее количество бракованных изделий, если изготовлена тысяча изделий.

5. При штамповке зубчатых колес вероятность нарушения стандартности равна 0,1. Найти вероятность того, что из пятисот изготовленных колесиков стандартных будет не менее четырехсот.

6. Вероятность того, что наугад взятое изделие окажется стандартным, равна 0,9. Сколько изделий нужно отобрать, чтобы с вероятностью 0,954 можно было утверждать, что доля стандартных изделий среди отобранных отклонится по абсолютной величине от 0,9 не более чем на 0,05?

7. Случайное отклонение размера детали от заданного – нормальная случайная величина с параметрами: а=0, =3. Годными являются те детали, для которых отклонение заключено в пределах от –5 до +5 мм. Сколько изделий следует изготовить, чтобы с вероятностью не меньшей, чем 0,99, среди них было не менее двух годных?

8. В партии из 100 телефонных аппаратов примерно 20 недействующих. Случайным образом отобраны 5 аппаратов. Найдите закон распределения числа недействующих аппаратов среди выбранных и дайте график функции распределения.

9. Случайное отклонение размера детали от заданного – нормальная случайная величина с параметрами а=0, =8. Изделие подлежит переделке, если отклонение больше 10 мм. Найти среднее число изделий, подлежащих переделке, если было изготовлено 1000 изделий.

10. Вероятность появления события в одном испытании р=0,6. Найти вероятность того, что при 1200 независимых испытаниях отклонение частоты от вероятности не превысит 0,05.

11. Случайное отклонение размера детали от заданного – нормальная величина с параметрами а=0, =3. Годными являются детали, для которых отклонение заключено в пределах от –10 до 10 мм. Сколько нужно изготовить изделий, чтобы с вероятностью не меньшей 0,99 среди них было не менее 5 годных?

12. Время безотказной работы двигателя – экспоненциальная случайная величина со средним 1000 часов. Найти среднее число двигателей, вышедших из строя за 2000 часов, если их было десять.

13. Ножки циркуля, каждая длиной 10 см, раздвинуты на угол , значения которого распределены в пределах от 0 до 180⁰ равномерно. Найти математическое ожидание расстояния между остриями ножек.

14. Из данной точки по заболоченному участку, имеющему форму круга радиуса 200 км, требуется проложить дорогу. Какова ожидаемая длина дороги, если направление ее выбирается произвольно?

15. При штамповке колесиков для часов вероятность нарушения стандартности равна 0,1. Найти вероятность того, что в пятистах изготовленных колесиках будет стандартных не менее 450.

16. Вероятность попадания точки М(х, у) на дугу окрудности х²+у²=1 пропорциональна длине дуги. Найти вероятность попадания случайной точки на Р=(х, у)х²+у²=1, у .

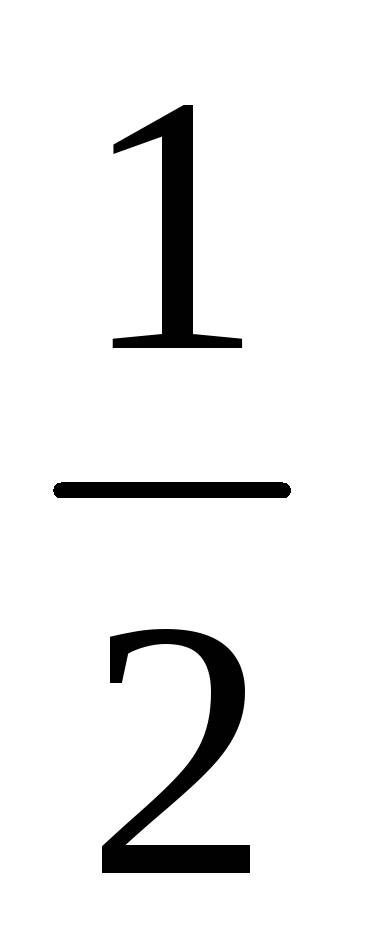17. В лотереи на 100 билетов разыгрываются две вещи, стоимость которых составляет 210 тыс.руб. и 50 тыс.руб. Найти закон распределения случайной величины ξ – числа испробованных лампочек. Найти математическое ожидание и дисперсию. Составить функцию распределения, построить ее график.

18. Ошибка взвешивания – случайная величина, распределенная нормально с параметрами m=10 г и σ=20 г. Найти вероятность того, что взвешивание произведено с ошибкой, не превышающей по модулю 25 г.

19. Имеется 3 лампочки, каждая из которых с вероятностью 0,3 имеет дефект. При включении дефектная лампочка перегорает и заменяется другой. Найти закон распределения случайной величины ξ – суммы выигрыша на два купленных билета. Найти математическое ожидание и дисперсию. Составить функцию распределения, построить ее график.

20. Случайная величина Х распределена равномерно на [2; 4]. Составить функцию плотности f(x). Построить график функции распределения F(x). Какова вероятность попадания Х в интервал (2,5; 3)?

21. Длина платья, выпускаемого предприятием, - случайная величина, распределенная нормально со средним 100 см и средним квадратическим отклонением 4 см. Найти вероятность того, что случайно выбранное платье будет иметь длину, меньшую, чем 90 см.

22. Отклонение размера изготавливаемой детали от стандарта – случайная величина, распределенная по нормальному закону с параметрами m=0 и σ=3 мм. Найти вероятность того, что размер изделия отклонился от стандартного на 6 мм по модулю.

23. Случайная величина  равномерно распределена на отрезке [0; ]. Построить график плотности f(х). Вычислить D(). Найти вероятность попадания случайной величины на промежуток [1; 2].

24. Функция распределения случайной величины  имеет вид

F(х)=А+В

Определить постоянные А и В. Найти плотность распределения вероятностей f(х). Построить графики F(x) и f(x).

25. Случайная величина  равномерно распределена на отрезке [-1; 4]. Построить график плотности f(х). Вычислить D(). Найти вероятность попадания случайной величины на промежуток [0; 3].

26. Случайная величина  равномерно распределена с М()=2 и D()=1. Найти интервал, на котором распределена случайная величина . Записать ее функцию распределения.

27. Случайная величина  равномерно распределена на отрезке [-0,5; 2,5]. Вычислить М() и D(). Что вероятнее: в результате испытания  окажется на промежутке [0; 1] или вне этого промежутка?

28. Случайная величина  равномерно нормально с М()=9 и D()25. Найти вероятность попадания  на интервал (5;14).

29. Испытывают три элемента, работающих независимо. Длительность времени безотказной работы каждого элемента распределена по показательному закону с λ=0,1. Найти вероятность того, что в промежутке времени откажет ровно 2 элемента.

30. Станок-автомат изготовляет валики, диаметр которых распределен по нормальному закону с математическим ожиданием 20 мм и дисперсией 0,04 . Найти интервал, в котором с вероятностью 0,997 будут заключены диаметры изготовленных валиков.

Задание 4. Выберите задачу Вашего варианта и решите (10 баллов).

1. Случайная величина Х распределена равномерно в интервале [-1; 1]. Построить график функции плотности f(х). Вычислить плотность распределения случайной величины =sinХ.

2. Случайная величина 0 обладает тем свойством, что ² распределена равномерно на [0; 1]. Найти закон распределения  и ее числовые характеристики.

3. Случайная величина  распределена равномерно в интервале (0; 2). Найти плотность распределения случайной величины =cos .

4. Случайная величина  распределена нормально с параметрами а=0, =1. Найти плотность распределения случайной величины =².

5. Случайная величина 0 распределена равномерно и обладает тем свойством, что ² распределена равномерно на [0; 1]. Найти закон распределения случайной величины  и ее числовые характеристики.

6. Случайная величина  обладает тем свойством, что случайная величина =ln  распределена нормально с параметрами а=0, =2. Найти закон распределения  и ее математическое ожидание.

7. Случайная величина  распределена равномерно в интервале 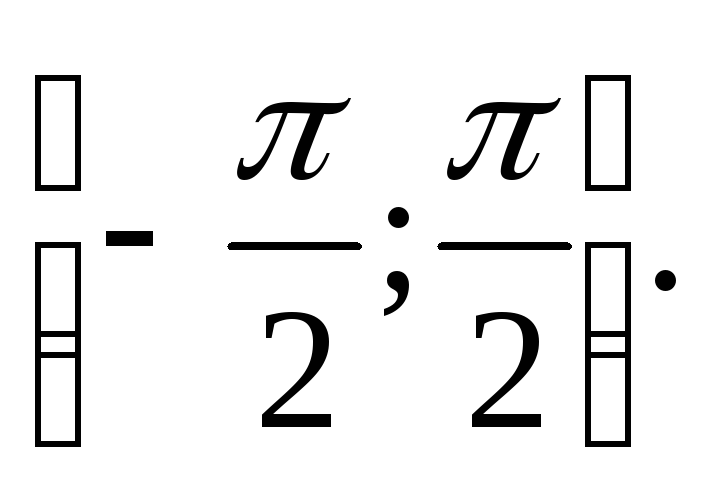Найти плотность распределения случайной величины cos .

8. Случайная величина  распределена равномерно на [-1; 1]. Найти распределение случайной величины =. Найти М() и D().

9. Случайная величина  распределена равномерно на [-1; 1]. Найти распределение случайной величины Y=sin(). Вычислить M(Y) и D(Y).

10. Найти закон распределения случайной величины =, если  - нормальная величина с параметрами а=0 и =1.

11. Случайная величина  распределена равномерно на [-1; 1]. Найти распределение случайной величины Y=cos(). Вычислить M(Y) и D(Y).

12. Случайная величина  распределена равномерно на [0; 1]. Найти распределение случайной величины =sin . Найти М().

13. Случайная величина  распределена нормально с параметрами а=0, =1. Найти распределение и числовые характеристики случайной величины =².

14. Через точку (0; 1) проведена прямая; угол наклона ее к оси ОХ является равномерной случайной величиной на промежутке [0; ]. Найти распределение абсциссы точки пересечения этой прямой с осью ОХ.

15. Случайная величина =е^ обладает тем свойством, что имеет равномерное распределение на промежутке [0; 1]. Найти функцию распределения  и ее плотность.

16. Случайная величина Х распределена равномерно в интервале [-1; 1]. Построить график функции плотности f(х). Вычислить плотность распределения случайной величины =cosХ.

17. Случайная величина 0 обладает тем свойством, что ³ распределена равномерно на [0; 1]. Найти закон распределения  и ее числовые характеристики.

18. Случайная величина  распределена равномерно в интервале (0; 2). Найти плотность распределения случайной величины =|sin|.

19. Случайная величина  распределена нормально с параметрами а=0, =1. Найти плотность распределения случайной величины =³.

20. Случайная величина 0 распределена равномерно и обладает тем свойством, что ³ распределена равномерно на [0; 1]. Найти закон распределения случайной величины  и ее числовые характеристики.

21. Случайная величина  обладает тем свойством, что случайная величина =2ln  распределена нормально с параметрами а=0, =2. Найти закон распределения  и ее математическое ожидание.

22. Случайная величина  распределена равномерно в интервале Найти плотность распределения случайной величины cos .

23. Случайная величина  распределена равномерно на [-1; 1]. Найти распределение случайной величины =. Найти М() и D().

24. Случайная величина  распределена равномерно на [-1; 1]. Найти распределение случайной величины Y=sin(). Вычислить M(Y) и D(Y).

25. Найти закон распределения случайной величины =, если  - нормальная величина с параметрами а=0 и =2.

26. Случайная величина  распределена равномерно на [-0,5; 0,5]. Найти распределение случайной величины Y=cos(). Вычислить M(Y) и D(Y).

27. Случайная величина  распределена равномерно на [0; 0,5]. Найти распределение случайной величины =sin . Найти М().

28. Случайная величина  распределена нормально с параметрами а=0, =2. Найти распределение и числовые характеристики случайной величины =².

29. Через точку (0; 1) проведена прямая; угол наклона ее к оси ОХ является равномерной случайной величиной на промежутке [0; 0,5]. Найти распределение абсциссы точки пересечения этой прямой с осью ОХ.

30. Случайная величина =е^ обладает тем свойством, что имеет равномерное распределение на промежутке [0; 0,5]. Найти функцию распределения  и ее плотность.

Задание 5. По заданной выборке значений случайной величины :

1. построить гистограмму относительных частот;

2. построить эмпирическую функцию распределения;

3. вычислить несмещенные оценки 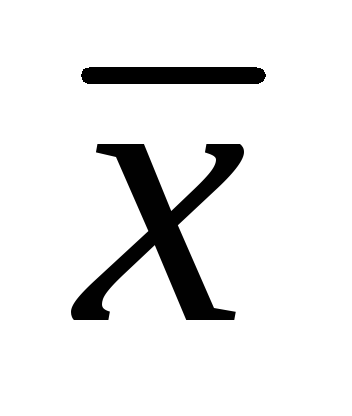и

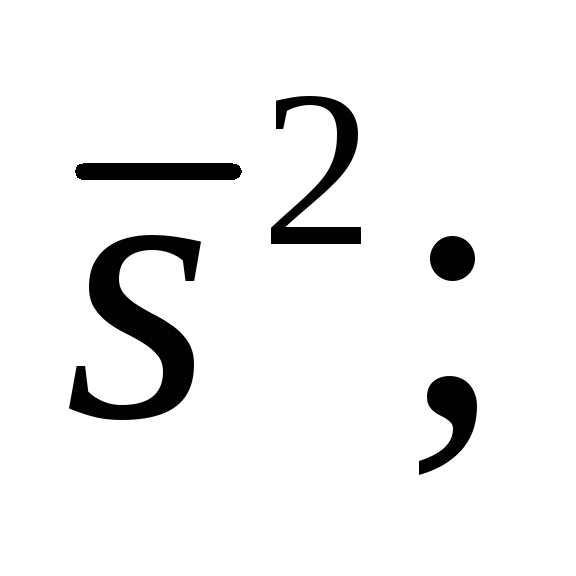
4. найти доверительный интервал для оценки математического ожидания случайной величины  с надежностью 0,95, считая  нормально распределенной (20 баллов).

1.

	0,455	0,4459	0,240	0,564	0,214	0,677	0,214	0,260
0,531	0,552	0,477	0,487	0,030	0,580	0,486	0,461	-0,020
0,023	0,806	0,662	0,276	0,467	0,571	0,484	0,574	0,437
0,305	0,581	0,782	0,373	0,603	0,769	0,136	0,720	-0,016
0,389	0,379	0,764	0,728	0,503	-0,130	0,135	0,720	-0,016
0,456	0,167	0,967	0,731	0,485	0,665