
- •Министерство образования и науки российской федерации
- •Лабораторная работа №1 операции над множествами
- •Теоретические сведения
- •Пример выполнения работы.
- •Контрольные вопросы
- •Примеры записи нечеткого множества
- •Пример выполнения работы.
- •Контрольные вопросы
- •Задание для лабораторной работы.
- •Лабораторная работа №3 бинарные отношения
- •Теоретические сведения
- •Технология выполнения работы.
- •Контрольные вопросы
- •Задание для лабораторной работы.
- •Лабораторная работа № 4 комбинаторные алгоритмы
- •Теоретические сведения
- •Технология выполнения работы.
- •Контрольные вопросы
- •Задание для лабораторной работы.
- •Лабораторная работа № 5 Машинное представление графа
- •Теоретические сведения
- •Технология выполнения работы.
- •Контрольные вопросы
- •Задание для лабораторной работы.
- •Лабораторная работа №6 алгоритмы построения кратчайших путей в графе и кратчайшего остова графа
- •Теоретические сведения
- •Пример выполнения работы.
- •Контрольные вопросы
- •Задание для лабораторной работы.
- •Лабораторная работа №7 алгоритмы построения эйлерова и гамильтонова цикла
- •Теоретические сведения
- •Пример выполнения работы.
- •Контрольные вопросы
- •Задание для лабораторной работы.
- •Лабораторная работа №8 совершенные нормальные формы булевых функций
- •Теоретические сведения
- •Технология выполнения работы.
- •Контрольные вопросы
- •Задание для лабораторной работы.
- •Библиографический список
Пример выполнения работы.
Даны множества;
 ,
, ,
, .
Найти:
.
Найти: ;
; ;
;
Даны
множества;
![]() ,
,![]() ,
,![]() .
Найти:
.
Найти:
 ;
; .
.
Решение.
 =
[1; 7)
=
[1; 7) 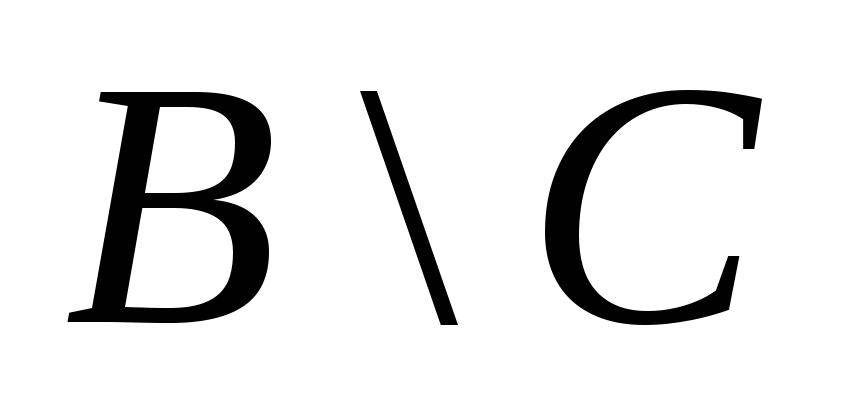 =
[4; 7)
=
[4; 7)
 =
[4; 5]
=
[4; 5] =
=
 =
{4}
=
{4}
 =
{1; 2}
=
{1; 2}
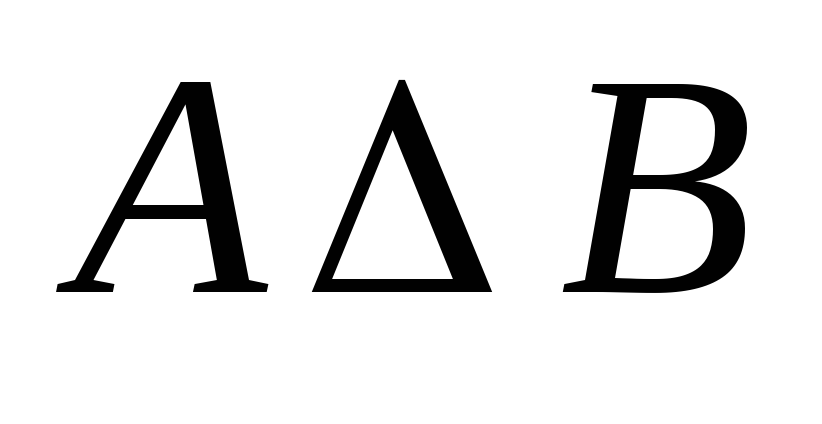 =
{1; 2; 4}
=
{1; 2; 4}
2. Доказать тождество A(B \ C) = (AB)\(AC).
Решение.
a) I способ. Докажем два нестрогих включения.
1) Прямое включение A(B \ C) (AB)\(AC).
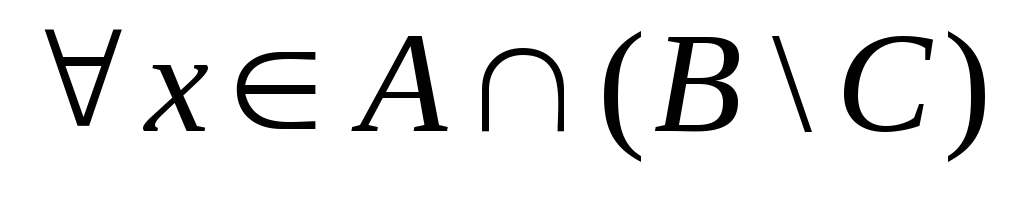

![]()
![]()
![]()
2) Обратное включение (A B)\(AC) A(B \ C).
![]()
![]()
![]()
![]() ,
так как в 1-м случае имеем противоречие
,
так как в 1-м случае имеем противоречие
![]()


b) II способ.
(AB)
\ (AC)
=
![]() =
=
![]() =
=
=
=![]() =
=
![]() =
=![]() =
A(B
\ C)
=
A(B
\ C)
3. Доказать включение множеств
(A1 A2) (B1 B2) (A1 B1) (A2 B2).
Решение.
![]()
![]()



![]()
![]()
4. Доказать, что A B C A B и A C.
Решение.
Докажем прямое следование, т.е. ABC AB и AC.
Если
справедливо включение
![]() ,
то
,
то
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Докажем обратное следование AB и AC ABC.
Выполнение
обоих включений условия
![]() означает, что
означает, что![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Контрольные вопросы
Дайте определения операций дополнения, пересечения, объединения, разности и симметричной разности множеств. Приведите примеры выполнения операций.
Сформулируйте отрицание принадлежности элемента множествам, построенных с помощью операций над множествами.
Приведите способы доказательства отношений нестрогого, строгого включения и равенства множеств.
Задание для лабораторной работы.
Для множеств варианта выполнить операции над множествами.
Доказать равенство множеств 2-мя способами:
по определению равенства множеств, доказав два нестрогих включения;
с использованием свойств операций.
Доказать включение множеств.
Доказать или опровергнуть утверждения о следовании или эквивалентности отношений между множествами.
Лабораторная работа №2
НЕЧЁТКИЕ МНОЖЕСТВА
Цель работы: изучение способов построения нечётких множеств и операций над нечёткими множествами.
Теоретические сведения
Нечеткое подмножество A универсального множества E определяется как множество упорядоченных пар A ={A(х)/х}, где A(х) – характеристическая функция принадлежности (или просто функция принадлежности), принимающая значения в некотором вполне упорядоченном множестве M (например, M =[0,1]). Функция принадлежности указывает степень (или уровень) принадлежности элемента x подмножеству A. Множество M называют множеством принадлежностей. Если M = {0,1}, то нечеткое подмножество A может рассматриваться как обычное или четкое множество.
Примеры записи нечеткого множества
Пусть E = {x1, x2, x3, x4, x5 }, M = [0,1]; A – нечеткое множество, для которого A(x1)=0,3; A(x2)=0; A(x3)=1; A(x4)=0,5; A(x5)=0,9. Тогда множество A можно представить в виде: A = {0,3/x1; 0/x2; 1/x3; 0,5/x4; 0,9/x5} или
A = 0,3/x1 0/x2 1/x3 0,5/x4 0,9/x5 или
|
A = |
|
Для построения функции принадлежности могут использоваться прямые методы, когда эксперт либо просто задает для каждого xE значение A(x), либо определяет функцию совместимости. При прямых методах используются также групповые прямые методы, когда, например, группе экспертов предъявляют конкретное лицо и каждый должен дать один из двух ответов: “этот человек лысый” или “этот человек не лысый”, тогда количество утвердительных ответов, деленное на общее число экспертов, дает значение "лысый" (данного лица). Как правило, прямые методы задания функции принадлежности используются для измеримых понятий, таких как скорость, время, расстояние, давление, температура и т.д., или когда выделяются полярные значения.
Косвенные методы определения значений функции принадлежности используются в случаях, когда нет элементарных измеримых свойств, через которые определяется интересующее нас нечеткое множество. Как правило, это методы попарных сравнений. Если бы значения функций принадлежности были нам известны, например, A(xi) = wi, i = 1, 2, ..., n, то попарные сравнения можно представить матрицей отношений A = {aij}, где aij = wi / wj (операция деления).
На практике эксперт сам формирует матрицу A, при этом предполагается, что диагональные элементы равны 1, а для элементов симметричных относительно диагонали aij = 1/aji, т.е. если один элемент оценивается в раз сильнее чем другой, то этот последний должен быть в 1/ раз сильнее, чем первый. Доказано, что в общем случае задача сводится к поиску вектора w, удовлетворяющего уравнению вида Аw = maxw, где max – наибольшее собственное значение матрицы A. Имеет место теорема Перрона, согласно которой для матрицы А с положительными элементами решение данной задачи существует и является положительным.
В
случае идеальной согласованности
экспертных оценок должно выполняться
соотношение
![]() .
(1)
.
(1)
В этом случае max совпадает с n – размерностью матрицы А. В случае нарушения условия (1) max меньше n. Таким образом, величина разности max – n может служить мерой согласованности экспертных оценок.
Выполнить операции с нечёткими множествами означает построить функции принадлежности множеств, получившихся в результате. Эти функции определяются с помощью функций принадлежности исходных множеств.
1. Дополнение.
![]()
2. Пересечение.
AB – наибольшее нечеткое подмножество, содержащееся одновременно в A и B;
A B(x) = min{A(x), B(x)}.
3. Объединение.
А В – наименьшее нечеткое подмножество, включающее как А, так и В, с функцией принадлежности
A B(x) = max {(A(x), B(x)}.
А
\ B
= А ![]() с функцией принадлежности:
с функцией принадлежности:
A\B(x) = min { A(x), 1 – B(x)}.
