Министерство образования и науки российской федерации

ФГБОУ ВПО

“Воронежский государственный УНИВЕРСИТЕТ

ИНЖЕНЕРНЫХ технологиЙ”

Ю.В. БУГАЕВ, И.Ю. ШУРУПОВА,

О.В. АВСЕЕВА, Л.А. КОРОБОВА

ДИСКРЕТНАЯ МАТЕМАТИКА

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

ВОРОНЕЖ

2015

ПРЕДИСЛОВИЕ

Процесс изучения дисциплины направлен на формирование следующих компетенций:

• способностью применять математический аппарат, в том числе с использованием вычислительной техники, для решения профессиональных задач (ПК-2);

• способностью применять методологию научных исследований в профессиональной деятельности, в том числе при работе над междисциплинарными и инновационными проектами (ПК-5).

• готовность использовать математические методы обработки, анализа и синтеза результатов профессиональных исследований (ПК-26).

В результате освоения дисциплины студент должен:

знать:

• основные понятия и методы дискретной математики;

• основные сведения о дискретных структурах, используемых в персональных компьютерах;

уметь:

• применять математические методы при решении профессиональных задач повышенной сложности;

владеть:

• методами построения математической модели профессиональных задач и содержательной интерпретации полученных результатов.

Лабораторная работа №1 операции над множествами

Цель работы: изучение операций над множествами и их свойств, методов доказательства утверждений теории множеств.

Теоретические сведения

Множеством называется совокупность некоторых предметов, объединенных общим признаком. Элементы множества – это те предметы, из которых состоит множество.

Для множеств вводятся следующие отношения.

Множество А нестрого включено в множество В (обозначается АВ) если для любого элемента хА, следует что хB. Нестрогое включение не исключает совпадения множеств.

Множество А строго включено в множество В (обозначается АВ) если:

1. АВ;

2. существует yB, такой, что yA.

Множество А совпадает с множеством В (А = В), если все элементы множества В являются элементами множества В и все элементы множества В являются элементами множества А, т.е.

(АВ и ВА)  (А = В).

Большинство утверждений теории множеств связано с равенством двух множеств и включением одного множества в другое. Поэтому детально разберёмся в методах доказательства этих фактов.

1. Доказательство нестрогого включения АВ. Для этого нужно доказать, что любой элемент x, принадлежащий множеству А одновременно является элементом множества В, т.е.

( x  А)   (x  В).

2. Доказательство строгого включения АВ состоит из двух частей:

1. АВ;

2.  y: y  B и y  A.

3. Доказательство равенства А = В сводится к доказательству двух включений А  В и В  А.

Дадим определения операций над множествами, используя способ задания множества характеристическим свойством или формулой теории множеств.

1. Дополнение :.

2. Пересечение :.

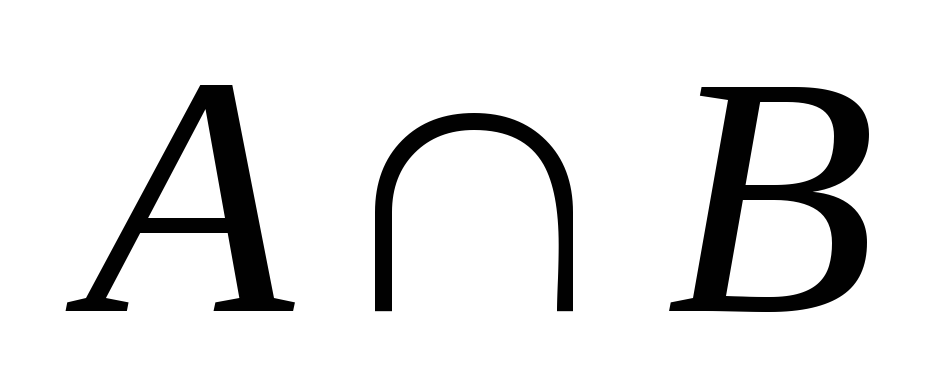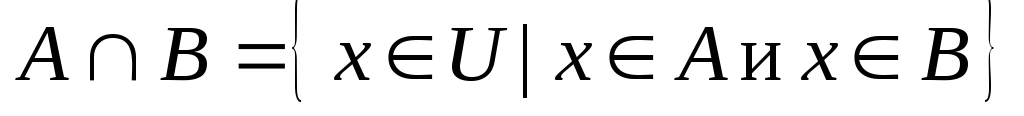3. Объединение :.

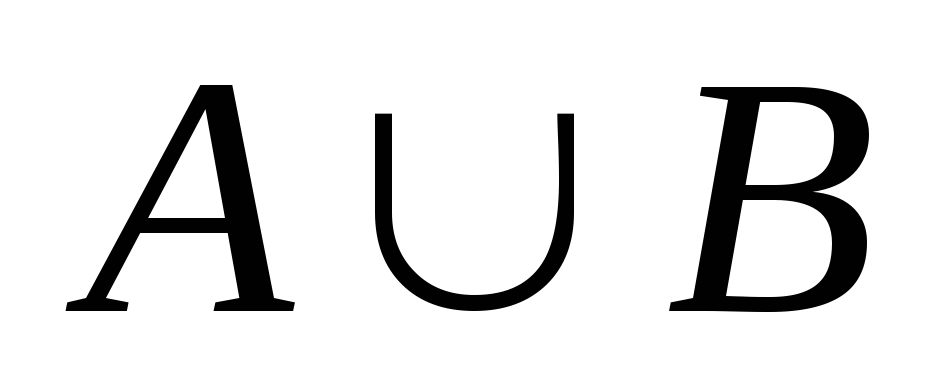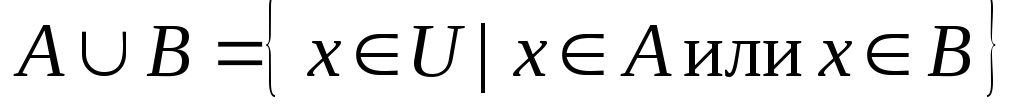4. Разность :.

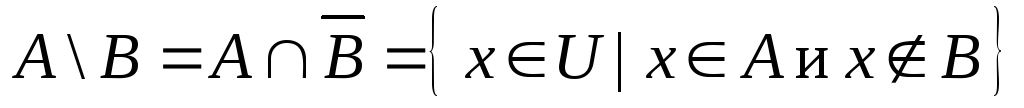5. Симметричная разность :.

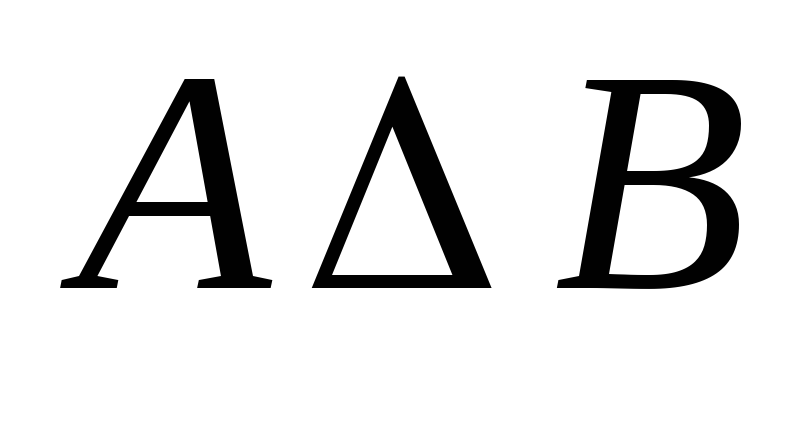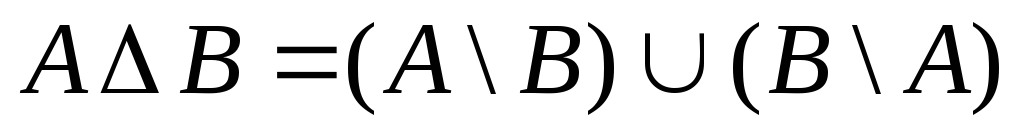В доказательствах будем также использовать следующие краткие обозначения, для того чтобы расписать принадлежность элемента множеству, построенному с помощью операций над множествами.



Фигурная скобка и запятая здесь, как и прежде, обозначает выполнение обоих свойств.



Квадратная скобка означает выполнение хотя бы одного из свойств. Таким образом, доказательство в дальнейшем распадается на два случая, для которых рассуждения проводятся отдельно, каждое в своей строке.





Распишем также, что означает, что элемент не принадлежит множеству, построенному с помощью операций над множествами.









Если из условия следует свойство о принадлежности элемента одному множества (например ) и ничего не известно относительно другого (B), которое участвует в формуле доказываемого утверждения, то необходимо рассмотреть оба случая и в обоих случаях вывести (или опровергнуть) требуемое свойство.

Утверждение вида эквивалентно включениямили.