
- •Введение
- •Программа курса математическая логика и терия алгоритмов
- •Логическое следствие в алгебре высказываний
- •2.1.3. Эквивалентные формулы алгебры высказываний
- •2.1.4. Дизъюнктивные и конъюнктивные нормальные формы в алгебре высказываний
- •2.1.5. Совершенные дизъюнктивные и конъюнктивные нормальные формы
- •Исчисление высказываний
- •Определение формального исчисления
- •Система аксиом и правил вывода
- •Теорема о дедукции в исчислении высказываний
- •Теорема о замене в исчисления высказываний
- •Свойства выводимых и эквивалентных формул исчисления высказываний
- •Основные эквивалентности исчисления высказываний
- •Полнота и непротиворечивость исчисления высказываний
- •Логика предикатов
- •Алгебраические системы
- •Пример 3. Построить подсистему алгебраической системы , порожденную множествомХ:
- •Формулы логики предикатов
- •Истинность формулы логики предикатов в алгебраической системе
- •2.3.4. Логическое следствие в логике предикатов
- •2.3.5. Эквивалентные формулы логики предикатов
- •2.3.6. Пренексная нормальная форма в логике предикатов
- •X(φ∧ψ)≡xφ∧ψ, X(φ∨ψ)≡xφ∨ψ,
- •X(φ∧ψ)≡xφ∧ψ, X(φ∨ψ)≡xφ∨ψ,
- •Xφ≡X(φ)xφ≡X(φ)
- •2.4. Исчисление предикатов
- •2.4.1. Система аксиом и правил вывода
- •2.4.2. Эквивалентные формулы исчисления предикатов
- •2.4.3. Теорема Геделя о полноте. Непротиворечивость исчисления предикатов
- •Элементы теории алгоритмов
- •2.5.1. Машины Тьюринга
- •2.5.2. Примитивно рекурсивные функции
- •2.5.3. Частично рекурсивные функции
- •Задания для домашних и контрольных работ
- •3.1. Совершенные дизъюнктивные нормальные формы, совершенные конъюнктивные нормальные формы
- •3.2. Логическое следствие в алгебре высказываний
- •Логическое следствие в логике предикатов
- •Частично рекурсивные функции
- •Список литературы
- •Основная литература
- •4.2. Дополнительная литература
- •Содержание
Полнота и непротиворечивость исчисления высказываний
Формула φ(x1,…,xn) ИВ называется тождественно истинной (обозначается ⊨φ), если φ(x1,…,xn) – тождественно истинная формула как формула алгебры высказываний.
Теорема 4 (о полноте). Формула φ ИВ доказуема тогда и только тогда, когда φ тождественно истинна:
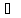 φ
φ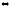 ⊨φ.
⊨φ.
Таким образом, для того чтобы установить, доказуема ли формула ИВ, достаточно составить ее таблицу истинности. Как известно, существует эффективный алгоритм построения таблицы истинности, и, значит, ИВ разрешимо. Кроме того, из теоремы о дедукции и теоремы о полноте легко следует, что отношение эквивалентности ≡ в АВ и ИВ совпадают.
Теорема 5 (о непротиворечивости). ИВ непротиворечиво.
Доказательство. По теореме о полноте любая формула, не являющаяся тождественно истинной, не доказуема в ИВ. Например, такой формулой является формула х∧¬х. Следовательно, ИВ непротиворечиво.
Схема аксиом называется независимой в исчислении, если хотя бы один ее частный случай не доказуем в исчислении без этой схемы.
Теорема 6. Схемы аксиом ИВ независимы.
Логика предикатов
Алгебраические системы
Часто объектом изучения в математике служит множество вместе с определенной на нем структурой. Например, поля, формирующие основу обычной арифметики, линейные пространства, обеспечивающие связь геометрических объектов с операциями над числами, множества с выделенными на них бинарными отношениями. Все эти структуры образуют алгебраические системы, представляющие собой некоторые миры с определенными на них законами. Перейдем к точному определению алгебраической системы.
Напомним, что п-местным
предикатом (отношением) на множестве А
называется любое
подмножество множества Аn;
п-местной алгебраической
операцией на множестве
А называется
функция F:An→A,
где
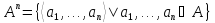 – n-я
декартова степень множества А.
Отметим, что поскольку
операция F является
функцией, для любого набора (x1,…,xn)
– n-я
декартова степень множества А.
Отметим, что поскольку
операция F является
функцией, для любого набора (x1,…,xn) An
результат применения
операции F(x1,…,xn)
однозначно определен.
Так как область значений операции F
лежит в множестве А,
то будем говорить,
что операция F
замкнута на
множестве А.
An
результат применения
операции F(x1,…,xn)
однозначно определен.
Так как область значений операции F
лежит в множестве А,
то будем говорить,
что операция F
замкнута на
множестве А.
Сигнатурой Σназывается совокупность предикатных и функциональных символов с указанием их местности. Константным символом или простоконстантойназывается 0-местный функциональный символ. Еслиα ‑ функциональный или предикатный символ, то его местность обозначается черезμ(α).Частоп-местные предикатные и функциональные символы будем обозначать соответственно черезР(n)иF(n), возможно с индексами. Если в рассматриваемой сигнатуре используются стандартные символы, такие, например, как + для операции сложения, ≤ для отношения порядка, | для отношения делимости, 0 для константного символа и другие, то мы просто пишемΣ={≤}, Σ={≤,+, ... , 0} и т.д.
Алгебраической системой сигнатурыΣназывается пара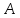 =
=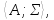 гдеА– непустое множество и
каждомуn-местному
предикатному (функциональному) символу
изΣпоставлен в соответствиеn-местный предикат
(соответственно операция) наА. МножествоА называетсяносителем, илиуниверсумом алгебраической системы
гдеА– непустое множество и
каждомуn-местному
предикатному (функциональному) символу
изΣпоставлен в соответствиеn-местный предикат
(соответственно операция) наА. МножествоА называетсяносителем, илиуниверсумом алгебраической системы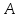 .
Предикаты и функции, соответствующие
символам изΣ, называются
ихинтерпретациями. Обозначать
интерпретации будем теми же буквами,
что и соответствующие символы сигнатуры,
возможно с индексомA.
Заметим, что интерпретацией любого
константного символа является некоторый
элемент изА. ЕслиΣ={α1,…,
αn} – конечная
сигнатура, то в записи
.
Предикаты и функции, соответствующие
символам изΣ, называются
ихинтерпретациями. Обозначать
интерпретации будем теми же буквами,
что и соответствующие символы сигнатуры,
возможно с индексомA.
Заметим, что интерпретацией любого
константного символа является некоторый
элемент изА. ЕслиΣ={α1,…,
αn} – конечная
сигнатура, то в записи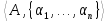 фигурные
скобки будем опускать.
фигурные
скобки будем опускать.
Пример 1. 1) Набор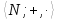 является алгебраической системой с
двумя двухместными операциями.
является алгебраической системой с
двумя двухместными операциями.
Набор
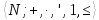 является алгебраической системой с
бинарным отношением ≤, двухместными
операциями +,
является алгебраической системой с
бинарным отношением ≤, двухместными
операциями +, ,
одноместной операцией':п→n+1
и нуль-местной операций 1.
,
одноместной операцией':п→n+1
и нуль-местной операций 1.Набор
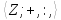 не является алгебраической системой,
поскольку деление не является операцией
на множестве
не является алгебраической системой,
поскольку деление не является операцией
на множестве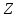 ,а элемент
,а элемент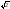 не принадлежит
не принадлежит .
.Набор
 является алгебраической системой, где
является алгебраической системой, где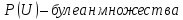
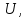 т.е.
множество всех подмножеств множества
т.е.
множество всех подмножеств множества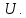
Алгебраическая система
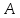 =
=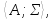 называетсяподсистемой системы
называетсяподсистемой системы =
=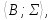 (обозначается
(обозначается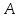

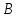 ),
если выполняются следующие условия:
),
если выполняются следующие условия:
а) А В;
В;
б) для любого функционального символа
F (n) Σи любых элементовa1,a2,…,an
Σи любых элементовa1,a2,…,an A
выполняется равенствоFA(a1,a2,…,an)=FB(a1,a2,…,an),
т.е. интерпретации символаFдействуют
одинаково на элементах изА;
A
выполняется равенствоFA(a1,a2,…,an)=FB(a1,a2,…,an),
т.е. интерпретации символаFдействуют
одинаково на элементах изА;
в) для любого предикатного символа
Р(n) Σ
справедливо равенствоP
Σ
справедливо равенствоP =
=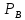 ∩An,
т.е. предикат
∩An,
т.е. предикат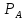 содержит в точности те кортежи предиката
содержит в точности те кортежи предиката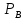 ,
которые состоят из элементов множестваА.
,
которые состоят из элементов множестваА.
Теорема 1. Если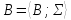 ‑ алгебраическая система,X
‑ алгебраическая система,X В,
X≠Ø, то существует
единственная подсистема
В,
X≠Ø, то существует
единственная подсистема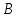 (Х)=
(Х)=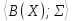 алгебраической системы
алгебраической системы
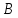 такая, чтоX
такая, чтоX В(Х)
и
В(Х)
и
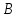 (Х)
(Х)
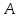 для любой подсистемы
для любой подсистемы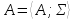 алгебраической системы
алгебраической системы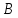 ,
для которойX
,
для которойX А.
А.
Подсистема
 (Х)
из теоремы 1 называетсяподсистемой
алгебраической системы
(Х)
из теоремы 1 называетсяподсистемой
алгебраической системы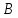 ,
порожденной множеством X.
,
порожденной множеством X.
Для описания элементов подсистемы
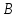 (Х)
определим индукцией по построению
понятиетерма сигнатурыΣ:
(Х)
определим индукцией по построению
понятиетерма сигнатурыΣ:
переменные и константные символы из Σсуть термы;
если F
 Σ‑ n-местный
функциональный символ,t1,t2,…,tn‑ термы, тоF(t1,t2,…,tn)‑ терм;
Σ‑ n-местный
функциональный символ,t1,t2,…,tn‑ термы, тоF(t1,t2,…,tn)‑ терм;никаких термов, кроме построенных по пп. 1,2, нет. Множество всех термов сигнатуры Σ обозначается черезТ(Σ).
Под сложностьютерма будем понимать число символов, входящих в терм.
Пример 2.
1) Термами сигнатуры Σ={+,∙,≤,0} будут, например,0, x, x+y, z∙(x+z)+0∙y, а x+y≤(0+х)x термом не является.
2) Если Σ={ƒ(3), g(1), h(2)} ‑ функциональная сигнатура, то выраженияh(ƒ(x1, x2, x3), g(x2)), g(ƒ(h(x1, x2), x1, g(x2))– термы, аh(x1, ƒ(x1, x3)) термом не является.
Пусть t(x1,…,xk)
‑ терм изT(Σ),
все переменные которого содержатся в
множестве {x1,…,xk},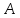 =
=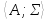 ‑ алгебраическая система.Значение
терма t на
элементахa1,…,ak
‑ алгебраическая система.Значение
терма t на
элементахa1,…,ak A
(t(a1,…,ak))
определяется по индукции:
A
(t(a1,…,ak))
определяется по индукции:
если t есть переменнаяxi (константный символс), то значениеt естьаi (с);
если t
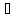 F(t1,…,
tn),
гдеF (n)
F(t1,…,
tn),
гдеF (n) Σ,
t1(x1,…,xk),…,tn(x1,…,xk)
Σ,
t1(x1,…,xk),…,tn(x1,…,xk) Т(Σ)
и значения термовt1,…,
tnна элементахa1,…,akравныb1,…,bn
то значение термаtестьF(b1,…,bn).
Т(Σ)
и значения термовt1,…,
tnна элементахa1,…,akравныb1,…,bn
то значение термаtестьF(b1,…,bn).
Теорема 2. Если =
=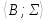 ‑ алгебраическая система,Ø≠X
‑ алгебраическая система,Ø≠X B,
тоB(Х)={t(a1,…,an)
| t
B,
тоB(Х)={t(a1,…,an)
| t T(Σ),
a1,…,an
T(Σ),
a1,…,an X}.
X}.
