
- •Введение
- •Программа курса математическая логика и терия алгоритмов
- •Логическое следствие в алгебре высказываний
- •2.1.3. Эквивалентные формулы алгебры высказываний
- •2.1.4. Дизъюнктивные и конъюнктивные нормальные формы в алгебре высказываний
- •2.1.5. Совершенные дизъюнктивные и конъюнктивные нормальные формы
- •Исчисление высказываний
- •Определение формального исчисления
- •Система аксиом и правил вывода
- •Теорема о дедукции в исчислении высказываний
- •Теорема о замене в исчисления высказываний
- •Свойства выводимых и эквивалентных формул исчисления высказываний
- •Основные эквивалентности исчисления высказываний
- •Полнота и непротиворечивость исчисления высказываний
- •Логика предикатов
- •Алгебраические системы
- •Пример 3. Построить подсистему алгебраической системы , порожденную множествомХ:
- •Формулы логики предикатов
- •Истинность формулы логики предикатов в алгебраической системе
- •2.3.4. Логическое следствие в логике предикатов
- •2.3.5. Эквивалентные формулы логики предикатов
- •2.3.6. Пренексная нормальная форма в логике предикатов
- •X(φ∧ψ)≡xφ∧ψ, X(φ∨ψ)≡xφ∨ψ,
- •X(φ∧ψ)≡xφ∧ψ, X(φ∨ψ)≡xφ∨ψ,
- •Xφ≡X(φ)xφ≡X(φ)
- •2.4. Исчисление предикатов
- •2.4.1. Система аксиом и правил вывода
- •2.4.2. Эквивалентные формулы исчисления предикатов
- •2.4.3. Теорема Геделя о полноте. Непротиворечивость исчисления предикатов
- •Элементы теории алгоритмов
- •2.5.1. Машины Тьюринга
- •2.5.2. Примитивно рекурсивные функции
- •2.5.3. Частично рекурсивные функции
- •Задания для домашних и контрольных работ
- •3.1. Совершенные дизъюнктивные нормальные формы, совершенные конъюнктивные нормальные формы
- •3.2. Логическое следствие в алгебре высказываний
- •Логическое следствие в логике предикатов
- •Частично рекурсивные функции
- •Список литературы
- •Основная литература
- •4.2. Дополнительная литература
- •Содержание
Теорема о дедукции в исчислении высказываний
Теорема 1 (о
дедукции). Пусть φ1,…,φm,φ,ψ
– формулы ИВ. Тогда φ1,…,φm,φ⊢ψ
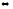 φ1,…,φm,⊢φ→ψ.
φ1,…,φm,⊢φ→ψ.
Пример 4. Покажем, что φ→ψ⊢¬ψ→¬φ;
Решение. По теореме о дедукции
φ→ψ⊢¬ψ→¬φ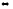 φ→ψ,
¬ψ⊢¬φ.
φ→ψ,
¬ψ⊢¬φ.
Строим вывод формулы ¬φ из формул φ→ψ,¬ψ:
1) φ→ψ (гипотеза);
2) ¬ψ (гипотеза);
(φ→ψ)→((φ→¬ψ)→¬ψ) (схема аксиом 9);
(φ→¬ψ)→¬φ (к пп. 1 и 3 применили правило вывода);
¬ψ→(φ→¬ψ) (схема аксиом 1);
φ→¬ψ (к пп. 2 и 5 применили правило вывода);
¬φ (к пп. 6 и 4 применили правило вывода).
Пример 5. Покажем, чтоφ→(ψ→χ)⊢ψ→(φ→χ)
Решение.По теореме о дедукции
φ→(ψ→χ)⊢ψ→(φ→χ)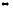 φ→(ψ→χ),ψ⊢(φ→χ)
φ→(ψ→χ),ψ⊢(φ→χ)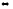 φ→(ψ→χ),ψ,φ⊢χ.
φ→(ψ→χ),ψ,φ⊢χ.
Строим вывод формулы χ из формул φ→(ψ→χ),ψ,φ:
1) φ→(ψ→χ) (гипотеза);
2) φ (гипотеза);
3) ψ (гипотеза);
4) ψ→χ (к пп. 2 и 1 применили правило вывода);
5) χ (к пп. 3 и 4 применили правило вывода).
Теорема о замене в исчисления высказываний
Формулы φ и ψ назовем эквивалентными (обозначим φ≡ψ), если
φ⊢ψ и ψ⊢φ.
Замечание 2. Для любых формул φ и ψ ИВ
φ≡ψ ⊢φ→ψ
и ⊢
ψ→φ.
⊢φ→ψ
и ⊢
ψ→φ.
Утверждение 1. Отношение ≡ является отношением эквивалентности на множестве формул ИВ, т.е. для любых формул φ, ψ, χ ИВ:
а) φ≡φ;
b)
φ≡ψ ψ≡φ;
ψ≡φ;
с) φ≡ψ,
ψ≡x φ≡x.
φ≡x.
Утверждение 2. Для любых формул φ, ψ, φ1, ψ1, φ2, ψ2 ИВ таких, что φ1≡ψ1 и φ2≡ψ2, имеют место эквивалентности:
φ1∧φ2≡ψ1∧ψ2, φ1∨φ2≡ψ1∨ψ2, φ1→φ2≡ψ1→ψ2, ¬φ1≡¬ψ1.
Теорема 2 (о замене). Пусть φ ‑ формула ИВ, ψ ‑ ее подформула, φ' получается из φ заменой некоторого вхождения ψ на формулу ψ' ИВ и ψ≡ψ'. Тогда φ≡φ'.
Свойства выводимых и эквивалентных формул исчисления высказываний
Утверждение 3. Пусть φ,ψ, χ – формулы ИВ. Тогда
⊢φ→φ;
φ∧ψ⊢φ;
φ∧ψ⊢ψ;
φ,ψ⊢φ
 ψ;
ψ;φ→ψ, ψ→χ⊢φ→χ (свойство транзитивности);
φ→(ψ→χ)≡ψ→(φ→χ) (свойство перестановочности посылок);
φ→(ψ→χ)≡φ∧ψ→χ (свойство соединения и разъединения посылок);
φ→ψ≡¬ψ→¬φ (свойство контрапозиции).
Доказательство. Пункты 1, 4, 6, 8 доказаны в примерах 13, 14, 16, 17.
Докажем пункт 7.
Покажем, что
φ→(ψ→χ)⊢φ ψ→χ.
По теореме о дедукции
ψ→χ.
По теореме о дедукции
φ→(ψ→χ)⊢φ ψ→χ
ψ→χ φ→(ψ→χ),
φ
φ→(ψ→χ),
φ ψ⊢χ.
ψ⊢χ.
Строим вывод формулы χ
из формул φ→(ψ→χ),
φ ψ:
ψ:
φ→(ψ→χ) (гипотеза);
φ
 ψ
(гипотеза);
ψ
(гипотеза); φ
 ψ→φ
(схема аксиом 3);
ψ→φ
(схема аксиом 3);φ (к пп. 2 и 4 применили правило вывода);
φ
 ψ→ψ
(схема аксиом 4);
ψ→ψ
(схема аксиом 4);ψ (к пп. 2 и 5 применили правило вывода);
ψ→χ (к пп. 4 и 1 применили правило вывода);
χ (к пп. 6 и 7 применили правило вывода).
Покажем,
что φ ψ→χ⊢φ→(ψ→χ).
По теореме о дедукции
ψ→χ⊢φ→(ψ→χ).
По теореме о дедукции
φ ψ→χ⊢φ→(ψ→χ)
ψ→χ⊢φ→(ψ→χ)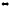 φ
φ ψ→χ,
φ⊢φ→χ
ψ→χ,
φ⊢φ→χ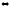 φ
φ ψ→χ,
φ,
ψ⊢χ.
ψ→χ,
φ,
ψ⊢χ.
Строим
квазивывод формулы χ
из формул φ ψ→χ,
φ,
ψ:
ψ→χ,
φ,
ψ:
φ
 ψ→χ
(гипотеза);
ψ→χ
(гипотеза);φ (гипотеза);
ψ (гипотеза);
φ
 ψ
(к п.п. 2 и 3 применили свойство 4);
ψ
(к п.п. 2 и 3 применили свойство 4);χ (к пп. 4 и 1 применили правило вывода).
Основные эквивалентности исчисления высказываний
Теорема 3. Пусть φ, ψ, χ ‑ формулы ИВ. Тогда имеют место следующие эквивалентности:
φ∧ φ≡φ, φ∨ φ≡φ (законы идемпотентности);
φ∧ ψ≡ψ∧ φ, φ∨ ψ≡ψ∨ φ (законы коммутативности);
(φ∧ψ)∧χ≡φ∧(ψ∧χ), (φ∨ψ)∨χ≡φ∨(ψ∨χ) (законы ассоциативности);
φ∧(ψ∨χ)≡(φ∧ψ)∨(φ∧χ), φ∨(ψ∧χ)≡(φ∨ψ)∧(φ∨χ) (законы дистрибутивности);
¬(φ∧ψ)≡¬φ∨¬ψ, ¬(φ∨ψ)≡¬φ∧¬ψ (законы де Моргана);
¬¬φ≡φ (закон двойного отрицания);
φ→ψ≡¬φ∨ψ;
⊢φ∨¬φ.
Доказательство.В примере 3 показано, чтоφ⊢¬¬φ. Покажем, что ¬¬φ⊢ φ. По теореме о дедукции
¬¬φ⊢
φ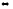 ⊢¬¬φ→
φ,
⊢¬¬φ→
φ,
что выполняется, т.к. ¬¬φ→ φ – частный случай схемы аксиом 10.
Докажем закон де Моргана ¬(φ∧ψ)≡¬φ∨¬ψ. Строим квазивыводформулы ¬(φ∧ψ)→¬φ∨¬ψ:
1) (¬(¬φ∨¬ψ)→φ)→((¬(¬φ∨¬ψ)→ψ)→(¬(¬φ∨¬ψ)→φ∧ψ)) (схема аксиом 5);
¬φ→¬φ∨¬ψ (схема аксиом 6);
¬(¬φ∨¬ψ)→¬¬φ (к п. 2 применили свойство контрапозиции);
¬¬φ→φ (схема аксиом 10);
¬(¬φ∨¬ψ)→φ (к пп. 3 и 4 применили свойство транзитивности);
¬(¬φ∨¬ψ)→ψ (получается аналогично формуле 5);
(¬(¬φ∨¬ψ)→ψ)→(¬(¬φ∨¬ψ)→φ∧ψ) (к пп. 5 и 1 применили правило вывода);
¬(¬φ∨¬ψ)→φ∧ψ (к пп. 6 и 7 применили правило вывода);
¬(φ∧ψ)→¬¬(¬φ∨¬ψ) (к п. 7 применили свойство контрапозиции);
¬¬(¬φ∨¬ψ)→(¬φ∨¬ψ) (схема аксиом 10);
¬(φ∧ψ)→¬φ∨¬ψ (к пп. 9 и 10 применили свойство транзитивности). Строим квазивывод формулы ¬φ∨¬ψ→¬(φ∧ψ):
(¬φ→¬(φ∧ψ))→((¬ψ→¬(φ∧ψ))→((¬φ∨¬ψ)→¬(φ∧ψ))) (схема аксиом 8);
φ∧ψ→φ (схема аксиом 3);
¬φ→¬(φ∧ψ) (к п. 2 применили свойство транзитивности);
φ∧ψ→ψ (схема аксиом 4);
¬ψ→¬(φ∧ψ) (к п. 4 применили свойство транзитивности);
(¬ψ→¬(φ∧ψ))→((¬φ∨¬ψ)→¬(φ∧ψ)) (к пп. 3 и 1 применили правило вывода);
7) (¬φ∨ψ)→¬(φ∧ψ) (к пп. 5 и 6 применили правило вывода).
Таким образом, закон де Моргана ¬(φ∧ψ)≡¬φ∨¬ψ доказан.
Формула ИВ, получаемая из ДНФ (КНФ) АВ заменой логических переменных на переменные ИВ, называется ДНФ (КНФ) ИВ.
Теорема 2. Для любой формулыφ ИВ существует ДНФ (КНФ)ψИВ такая, чтоφ≡ψ.
