3.3. Числовые характеристики дискретных

случайных величин

Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на их вероятности:

. (3.1)

Математическое ожидание оценивает среднее значение случайной величины.

Свойства математического ожидания:

1. М(С) = С.

2. М(СХ) = СМ(Х).

3. М(Х + Y) = M(X) +M(Y).

4. М(ХY) = M(X)M(Y), случайные величины X и Y независимые.

Отклонением случайной величины X от ее математического ожидания M(X) называется случайная величина X – M(X).

Дисперсией случайной величины X называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

. (3.2)

Дисперсия характеризует степень разброса значений случайной величины относительно математического ожидания.

Свойства дисперсии:

1. D(C) = 0.

2. D(CX) = C²D(X).

3. D(X  Y) = D(X) + D(Y).

Дисперсию случайной величины удобно вычислять по формуле

. (3.3)

Средним квадратическим отклонением случайной величины называется корень квадратный из дисперсии, т. е.

. (3.4)

Так же как и дисперсия среднее квадратическое отклонение характеризует степень разброса значений случайной величины относительно математического ожидания. Единицы измерения M(X) и совпадают,D(X) измеряется в единицах квадратных.

Пример 3.9. Найти математическое ожидание, дисперсию, среднее квадратическое отклонение дискретной случайной величины, ряд распределения которой получили в примере 3.8.

Решение

В примере 3.8 получили приведенный ниже ряд распределения

X	0	1	2	3	4
pi

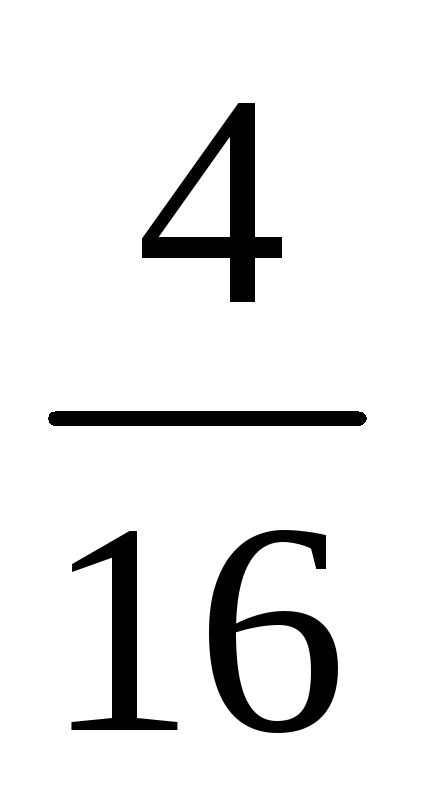
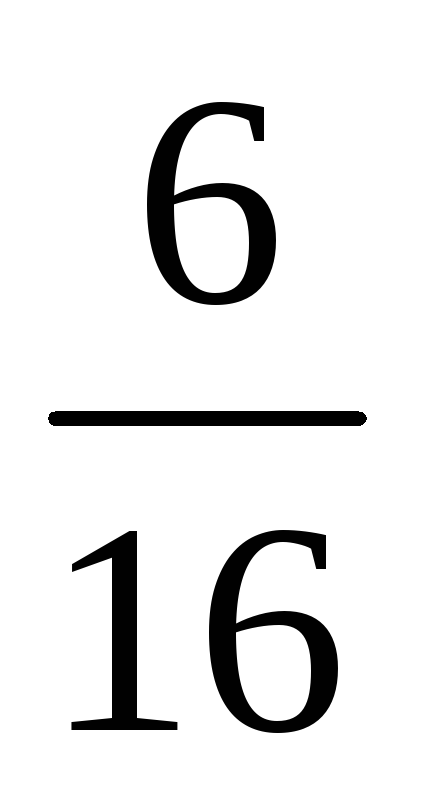
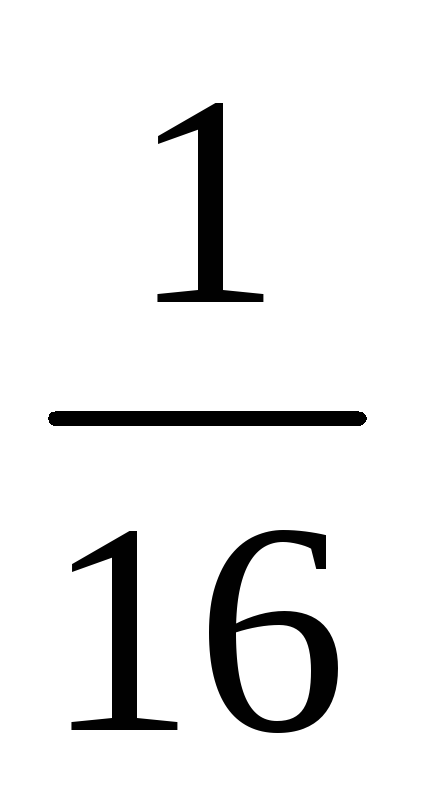
1. По формуле (3.1) найдем математическое ожидание:

.

2. По формуле (3.3) определим дисперсию:

.

.

3. По формуле (3.4) найдем среднее квадратическое отклонение:

.

Пример 3.10. Найти математическое ожидание случайной величины Y = 3X + 5, если M(X) = 2.

Решение

Используя свойства математического ожидания, получим:

_{Ответ: 11.}

Пример 3.11. Найти дисперсию случайной величины Y = 3X + 5, если D(X) = 4.

Решение

Используя свойства дисперсии, получим:

.

_{Ответ: 36.}

Тест 3.5.математическое ожидание дискретной случайной величины, заданной рядом распределения

x	-1	0	1
pi	0,1	0,7	0,2

равно:

1) –2;

2) 0;

3) 1;

4) 0,014;

5) 0,1.

Тест 3.6. Дисперсия дискретной случайной величины, заданной рядом распределения

x	-1	0	1
pi	0,1	0,7	0,2

равна:

1) ;

2) ;

3) ;

4) ;

5) .

Тест 3.7. Известно математическое ожидание случайной величины X : M(X) = 1. Тогда математическое ожидание случайной величины Y = 2 + 7X будет равно:

1) 2;

2) 9;

3) 1;

4) 7;

5) 0.

Тест 3.8. Дисперсия случайной величины равна 2. Тогда дисперсия случайной величиныбудет равна:

1) 2;

2) 9;

3) 49;

4) 10;

5) 50.

3.4. Непрерывные случайные величины

Функция распределения непрерывной случайной величины F(x) = P(X < x) является непрерывно дифференцируемой, за исключением конечного числа точек.

Все свойства функции распределения дискретной случайной величины выполняются и для функции распределения непрерывной случайной величины.

Производная от функции распределения F(x) называется плотностью распределения вероятностей (или дифференциальной функцией распределения):

.

Пример 3.12. Дана функция распределения непрерывной случайной величины

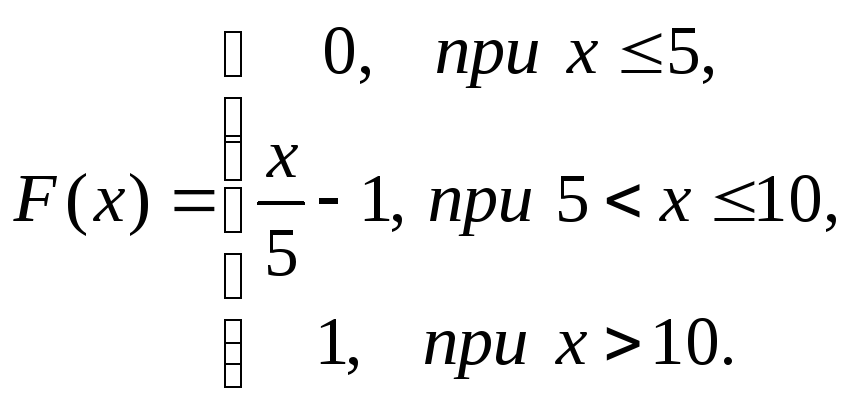
Найти плотность распределения этой случайной величины.

Решение

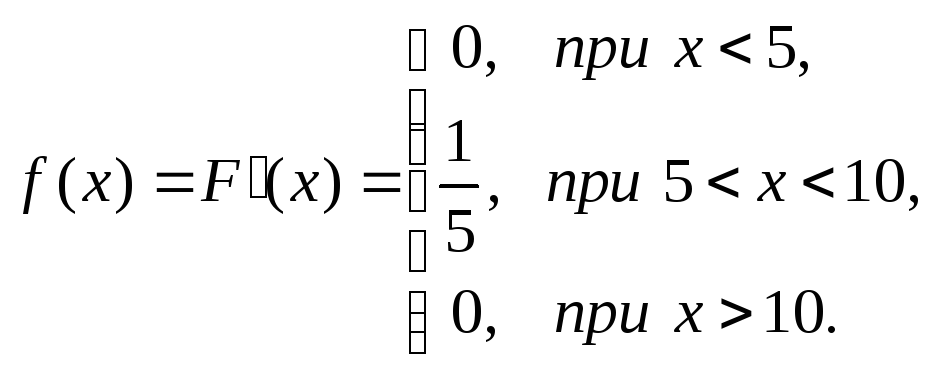
При x= 5 имеем:,.

Так как , тоне существует.

При x= 10 имеем:,.

Так как , тоне существует.

Тест 3.9. Дана функция распределения непрерывной случайной величиныX:

Дифференциальная функция распределения (плотность распределения) f(x) будет равна:

1) 0;

2) 1;

3)

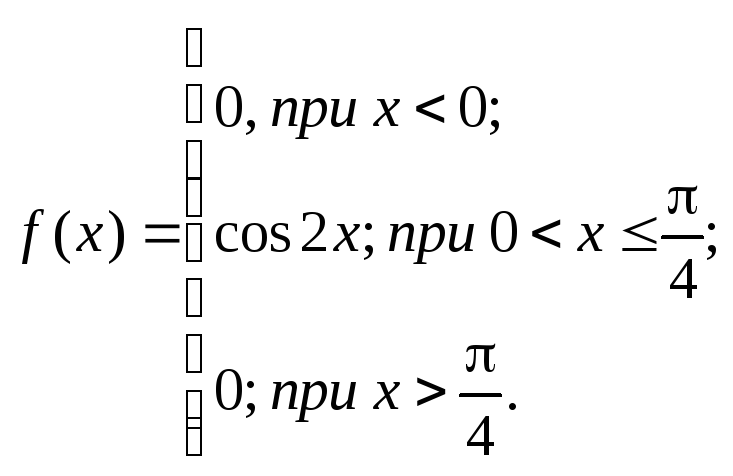
4)

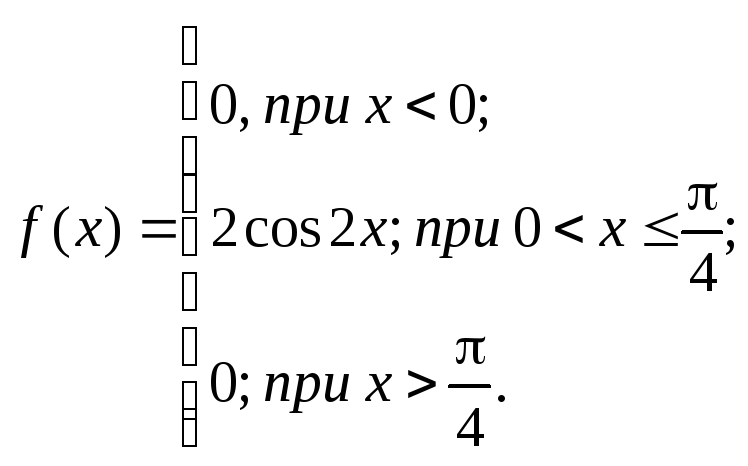
5)

Зная плотность распределения, можно найти функцию распределения по формуле

Вероятность того, что непрерывная случайная величина x примет значение, принадлежащее интервалу (a;b), определяется равенством

,

.

Пример 3.13. Дана функция распределения непрерывной случайной величины X

Найти вероятность того, что X примет значение, принадлежащее интервалу , черези.

Решение

1. Воспользуемся формулой

.

По условию ;; на этом интервале . Следовательно, искомая вероятность

.

2. Найдем плотность распределения:

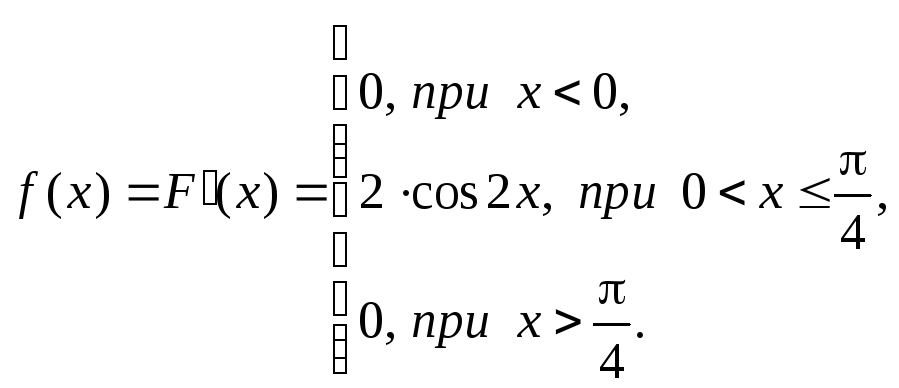
Воспользуемся формулой .

Тогда

.

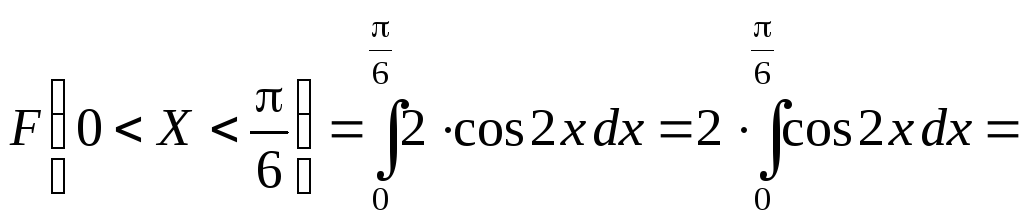
Ответ: .

Тест 3.10. Дана функция распределения непрерывной случайной величины

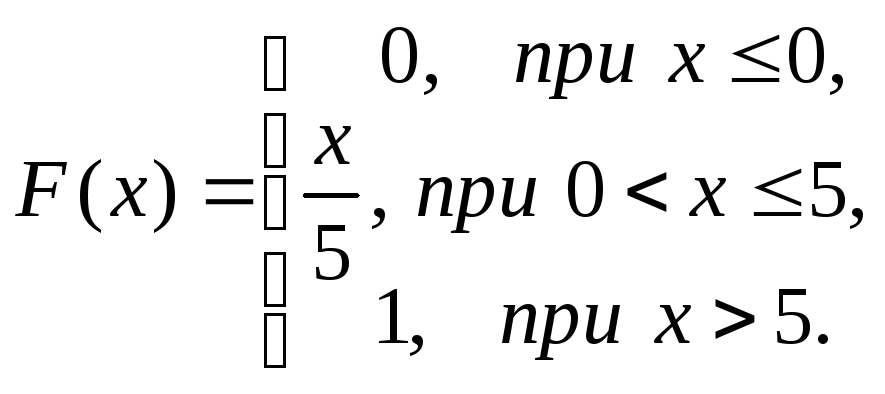
Вероятность того, что случайная величина примет значение, заключенное в интервале (3;4), равна:

1) 0;

2) ;

3)

4) 1;

5) .