Задачи для самостоятельного решения
1. Найти дисперсию, среднее квадратическое отклонение случайной величины X (число появления события A в 100 независимых испытаниях), если в каждом испытании вероятность наступления события А равна 0,7.
Ответ:21.
2. Найти начальные центральные моменты первого, второго и третьего порядков случайной величины X, которая задана законом распределения:
|
X |
2 |
3 |
|
P |
0,4 |
0,6 |
Ответ: 1 = 2,6, 2 = 7, 3 = 19,4; 1 = 0, 2 = 0,24, 3 = –17,624.
3. Монету бросают 4 раза. Найти математическое ожидание и дисперсию числа появлений герба.
Ответ: M(X) = 2, D(X) = 1.
4. Рабочий обслуживает 4 станка. Вероятность того, что первый станок не требует наладки равна 0,9, для второго – 0,8, для третьего – 0,75, четвертого – 0,7. Найти математическое ожидание числа станков, не требующих наладки.
Ответ: 3,15.
5. Найти математическое ожидание случайной величины Z = 3X + + 4Y, если M(X) = 2, M(Y) = 6.
Ответ: M(Z) = 30.
6. Дискретная случайная величина X принимает три возможных значения: x1 = 4 с вероятностью p = 0,5; x2 = 6 с вероятностью p = 0,34 и x3 с вероятностью p3. Найти x3 и p3, зная, что M(X) = 8.
Ответ: x3 = 21, p3 = 0,2.
2.4. Плотность распределения
Непрерывной называют такую случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.
Вероятность того, что непрерывная случайная величина X примет значение C, равна нулю (P(X = C) = 0), так как это есть вероятность того, что из бесконечного множества значений выпадает наперед заданное. Следовательно, значениям X в этом случае нельзя ставить в соответствии их вероятности. Закон распределения непрерывной величины Х может быть задан с помощью функции распределения:
F(x) =P(–
<X<x). (50)
Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения:
. (51)
Плотность распределения называют также дифференциальной функцией распределения. Зная плотность распределения, можно найти функцию распределения
. (52)
Плотность распределения вероятностей обладает следующими свойствами:
1.
. (53)
2.
. (54)
3.
. (55)
4.
,
если
. (56)
График дифференцируемой функции называют кривой распределения. Дифференциальная функция существует только для непрерывных случайных величин, а интегральная как для непрерывных, так и для дискретных случайных величин. Функция f(x) вероятностью не является.
Пример
2.11. Плотность
распределения случайной величины X
задана функцией
.
Найти значение параметра c.
Решение. Используя формулу (54) получим:
;
;
;
.
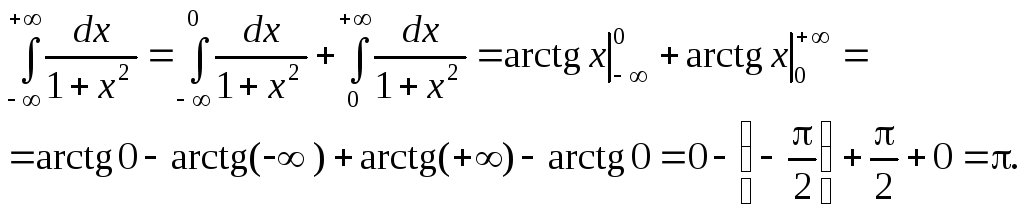
Пример 2.12. Найти вероятность того, что в результате испытания случайная величина X примет значение из интервала (1;2), если плотность вероятности величины X задана следующей функцией:
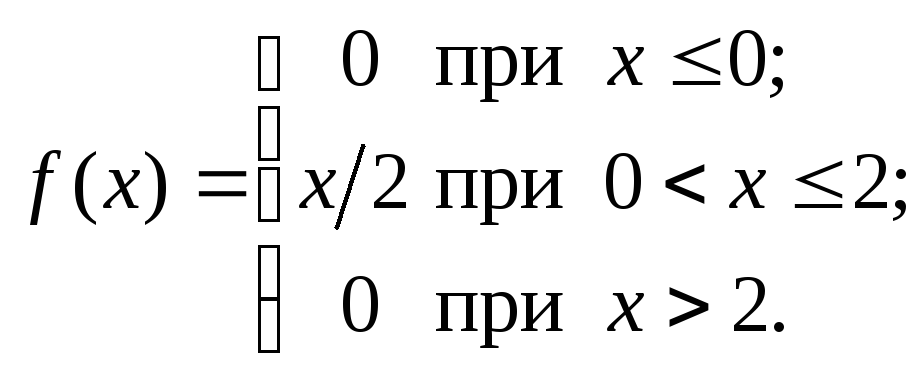
Решение.
.
Пример 2.13. Найти плотность распределения случайной величины X, функция распределения которой имеет вид:
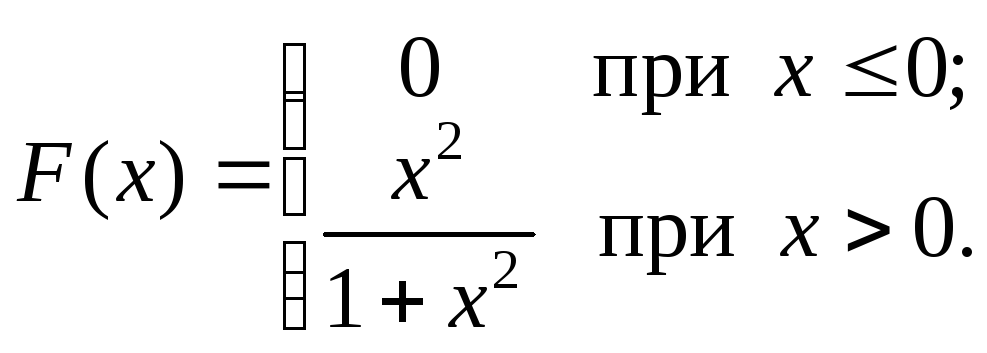
Решение.
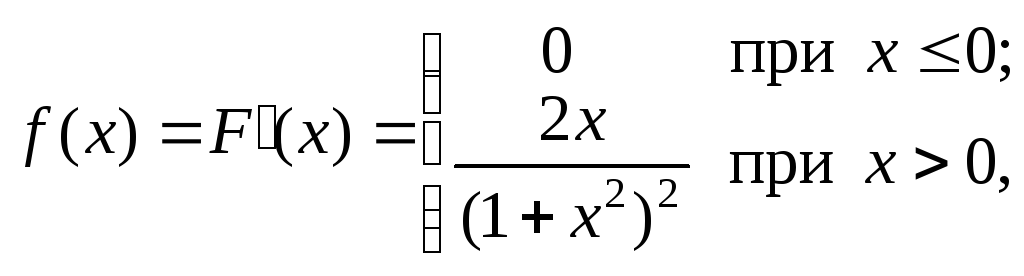
где
.
Пример 2.14. Найти функцию распределения F(x), если плотность распределения случайной величины X равна:
Решение. Используя формулу (52) получим:
при
;
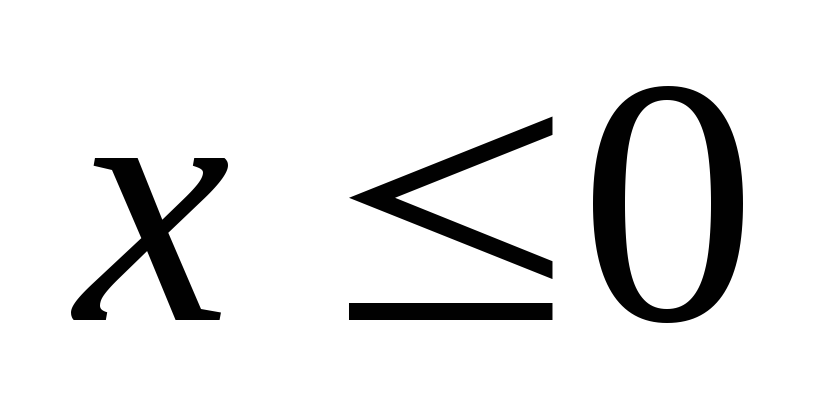
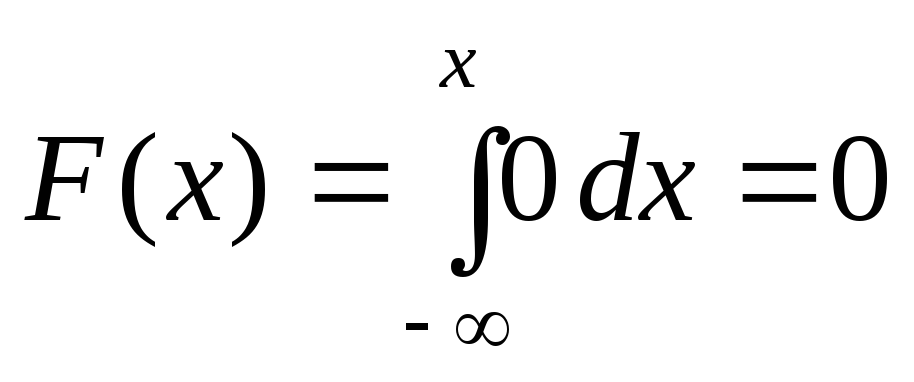при
;
при
.
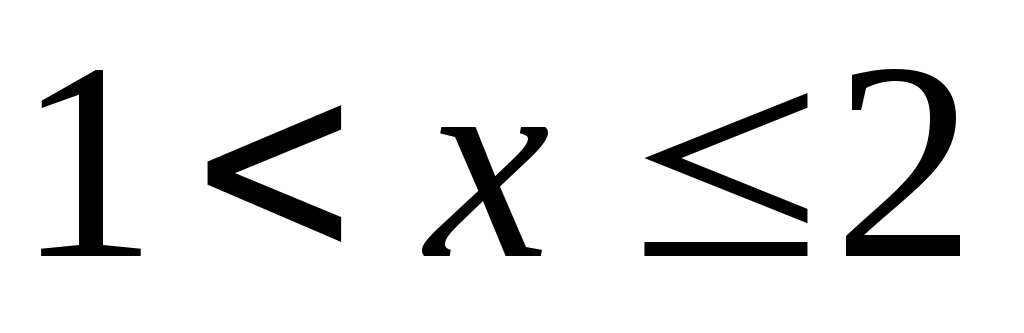
Искомая функция распределения имеет вид: x > 2,
= 0,5 + 4 – 2 – 2 + 0,5 + 0 = 1.
.
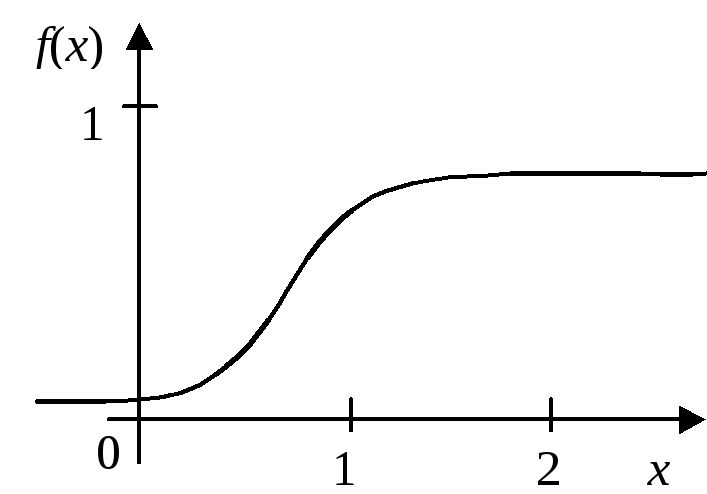
Графики функций f(x) и F(x) отражены на рис. 2.3 и 2.4.
|
Рис. 2.3 |
Рис. 2.4 |
