Лекция 6

2.3. Представление синусоидальных функций времени комплексными числами

Применение векторных диаграмм для анализа цепей переменного тока, несмотря на простоту и наглядность, не всегда дает достаточную точность при расчетах. Комплексный метод объединяет в себе простоту векторных диаграмм с возможностью производить расчеты с любой заданной степенью точности. Этот метод позволяет при различных операциях с электрическими величинами учитывать как абсолютные значения этих величин (модули), так и их фазы (аргументы).

Комплексный метод основан на представлении векторов в комплекс-ной плоскости и на записи их комплексными числами. Это позволяет для цепей синусоидального тока применять законы Ома и Кирхгофа и вытекающие из них методы расчета цепей в той же форме, что и для цепей по­стоянного тока. Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое можно записать в алгебраической, тригонометрической и показательной форме.

Комплексная плоскость представляет собой прямоугольную систему

координат (рис. 2.7), подобно плоскости декартовых координат. Ось абсцисс на комплексной плоскости является вещественной осью и обозначается (+); (—), а ось ординат — мнимой и обозначается (+j), (-j), где . По вещественной оси откладывают действительную часть комплексного числаа, а по мнимой оси — мнимую часть комплекс­ного числа jb. Комплексную величину отмечают точкой (и т. д.) или подчеркивают снизу (Z, Y, γ т. д.). Комплексным числом (или просто комплексом) называют сумму действительного и мнимого чисел, напри­мер для рис. 2.7

(2.12)

где — модуль комплекса, равный длине вектора, изображающего комплексное число; α = arctg (b/а) — аргумент комплексного числа, т. е. угол между осью вещественных чисел и вектором, изображаю­щим комплексное число;— формула Эйлера; е — основание натурального логарифма.

В (2.12) представлены три формы записи комплексного числа: алгеб­раическая, тригонометрическая и показательная.

За положительное направление вращения вектора на комплексной плоскости принимают направление вращения против часовой стрелки. Поэтому положительный угол α откладывают от полуоси вещественных чисел против часовой стрелки, а отрицательный угол (— α) —по часо­вой стрелке. Если имеется отрицательный угол (— α), то формула Эйлера принимает вид

Таким образом, в общем виде имеем следующие выражения для комплексного числа:

Если вектор R повернуть из положения 1 в положение 2 (рис. 2.7), то в комплексной форме это запишется как

Следовательно, умножение комплексного числа на множитель типаравносильно повороту вектора на комплексной плоскости на угол ±β Поэтому множительназывают поворотным или оператором поворота вектора.

Рассмотрим формулу Эйлера, считая, что

Умножение комплексного числа на ±j равносильно повороту вектора на комплексной плоскости на угол ±π/2. Если взять, например, комплексто, умножив его на j, получим что

при его графическом построении на комплексной плоскости соответствует повороту вектора R на угол π/2 в положительном направлении, т, е. про­тив часовой стрелки.

Считая угол поворотного множителя функцией времени, т. e. получаем множитель, или оператор вращения Это означает, что если вектор умножить на е^jωt, то он станет радиус-вектором, вращающим­ся со скоростью ω:

Это выражение называется комплексной функцией времени или комплексным мгновенным значением.

Производная от комплексной функции времени равна

(2.13) Интеграл от комплексной функции времени

(2.14)

Выражения (2.13) и (2.14) показывают, что дифференцирование и интегрирование комплексных функций времени можно заменить соот­ветственно умножением или делением их на jω.

Операции сложения, вычитания, умножения и деления синусоидаль­ных функций производят путем сложения, вычитания, умножения и деле­ния векторов на комплексной плоскости.

Два комплексных числа будут равны, если равны их действительные и мнимые части, т. е. когда Два комплексных числа и называютсопряженными, причем (a + jb)(a – jb) = a² + b².

Произведение комплексных чисел, например является комплексным числом, которому на комплексной плоскости соответствует вектор R:

(2.15)

Итак, вектор произведения комплексных чисел имеет длину, равную произведению их модулей, а угол γ относительно вещественной положи­тельной оси равен сумме углов векторов сомножителей.

При делении комплексных чисел получается комплексное число, модуль которого равен частному от деления модулей, а угол — разности углов исходных комплексных чисел:

(2.16)

Рассмотрим на комплексной плоскости вращающийся вектор , изображающий синусоидальное напряжение и составляющий с осью вещественных чисел угол(рис. 2.8). Запишем этот вектор в виде комплексного числа в трех формах:

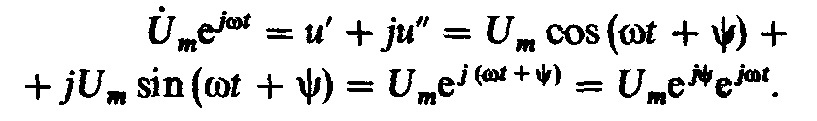(2.17)

Здесь U_mе^j = — комплексное число, соответствующее положению

вектора в начальный момент времени и называемое комплексной амплиту-дой; \|/ — начальная фаза; е^jt — множитель вращения, который является оператором поворота вектора на угол t относительно начального положения вектора.

Таким образом, мнимая составляющая комплексного числа и вектора на комплексной плоскости представляет собой синусоидальное напряжение

(2.18)

Здесь символ Im означает, что от комплексной функции времени, записанной в квадратных скобках, берется только мнимая часть.

В уравнении (2.17) вещественная часть комплексного числа и вектора на комплексной плоскости представляет собой косинусоидальную функцию времени, мгновенное значение которой

Здесь символ Re обозначает вещественную часть комплексной функции времени, записанной в скобках. На рис. 2.8 мгновенное значение и' можно определить графически как проекцию вращающегося векторана ось вещественных чисел.

Обычно на комплексной плоскости откладывают комплексы дей-ствующих значений, т. е. при расчете цепей синусоидального тока необ-ходимо знать только действующие значения для синусоидальных функций времени и их сдвиг по фазе друг относительно друга.

Если выражениеесть комплексная амплитуда напряжения, то соответственно комплексное действующее значение напряжения, или просто комплексное напряжение,

Этот комплекс напряжения на комплексной плоскости изобра-жается неподвижным вектором . Если необходимо получить выражение для мгновенного значения напряжения (э. д. с., тока), зная соответственно значение комплексного напряжения , то для этого вначале необходимо заданный комплекс умножить на , получив тем самым комплексную амплитуду, а затем, умножив еще наe^jt получить комплексную функцию времени. Взяв от комплексной функции времени мнимую часть, находят искомое мгновенное значение и".