ЛОГИНОВ Лекция 3

Лекция 3

Гармонический осциллятор

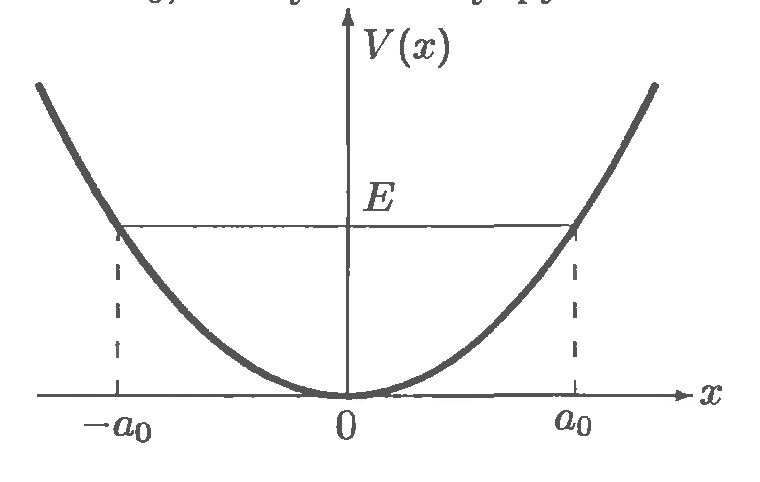
Постановка задачи. Рассмотрим стационарные состояния квантовой частицы массы движущейся в одномерном упругом поле с потенциальной энергией где -коэффициент жесткости. На рисунке показана полная энергия частицы . Точки поворота, в которых кинетическая энергия равна нулю, имеют координаты

Гамильтониан рассматриваемой системы имеет вид

. (s.1)

Стационарные состояния будем определять из решения следующего уравнения Шредингера

(s.2)

Здесь введена круговая частота В уравнении (s.2) перейдем к безразмерным переменным. Положим где Тогда гамильтониан (s.1) принимает вид

. (s.3)

Далее для решения спектральной задачи можно поступать обычным образом, решая непосредственно дифференциальное уравнение . Поступим, однако, иначе для чего используем представление операторов рождения и уничтожения.

Введем оператор

(s.4)

Этот оператор не является эрмитовым оператором. Эрмитово сопряженный оператору оператор имеет вид

(s.5)

Коммутатор операторов и равен

(s.6)

Действительно

С другой стороны

В представлении операторов гамильтониан модели квантового гармонического осциллятора принимает простой вид

(s.7)

Здесь введен оператор

(s.8)

Таким образом, гамильтониан системы- есть линейная функция оператора Решение интересующей нас спектральной задачи свелась к определению собственных функций и собственных значений более простого оператора .

Спектральная задача для оператора :

(s.9)

Исследуем свойства оператора .

1. Собственные значения оператора неотрицательны.

В самом деле, предполагая, что функции нормированы на единицу, находим

где Равенство нулю имеет место если Из доказательства следует, что спектр оператора , а следовательно и гамильтониана ограничен снизу. Ограничения связано с тем, что оператор потенциальной энергии имеет в точке минимум.

2. Предположим, что функция является собственной функцией оператора с собственным значением . Можно показать, что

Таким образом, если то , очевидно, собственная функция оператора , а - его собственное значение. Если то с учетом утверждения 1 следует

3. Покажем, что

(s.10)

где - собственная функция оператора , соответствующая наименьшему собственному значению . Так как - наименьшее собственное значение, то в соответствие с утверждением 2 , получаем

и

Собственное значение представляет собой также среднее значение оператора в состоянии :

Следовательно, наименьшее собственное значение оператора равно нулю.

4. Собственные значения оператора -целые числа.

В самом деле, пусть - собственное значение оператора , лежащее в интервале , а - соответствующая собственная функция. Подействуем последовательно раз оператором на функцию . В результате получим последовательность собственных значений:. Последнее в этой последовательности собственное значение лежит в интервале . Ему соответствует собственная функция . Подействуем оператором на функцию , получим

Результат обусловлен тем, что действие оператора приводит к собственному значению , что невозможно (см. утверждение 1). Собственное значение -есть среднее значение оператора в состоянии :

Отсюда, заключаем, что

(s.11)

При - наименьшее собственное значение.

5. Пусть - собственная функция оператора с собственным значением Покажем, что функция - также является собственной функцией оператора с собственным числом В самом деле, используя коммутационное соотношение (s.6) получаем

(s.12)

Из-за неограниченности операторов кинетической и потенциальной энергии спектр оператора сверху неограничен.

Операторы получили название операторов рождения и уничтожения частиц, а оператор - называется оператором числа частиц. Подобные операторы широко используются в различных разделах квантовой механики. Под частицей следует понимать не реальную частицу, а квант с энергией

Пусть собственная функция оператора числа частиц, тогда

(s.13)

Следовательно, задача о стационарных состояниях квантового гармонического осциллятора принимает вид

(s.14)

с дискретным спектром энергии , который с учетом (s.13) имеет вид:

(s.15)

Число называется главным квантовым числом. Спектр энергии (s.15) эквидистантный, т.е. расстояние между соседними уровнями постоянно и не зависит от

Отметим, что с помощью операторов рождения и уничтожения спектр энергии определен минуя непосредственное решение спектральной задачи (s.14), а используя только коммутационное соотношение (s.6).

Определим из (s.14) собственные функции . Считаем, что собственные функции ортогональны и нормированы на единицу, т.е.

Рассмотрим действие операторов на волновую функцию . Так как

Коэффициент подлежит определению. Рассмотрим скалярные произведения

,

Таким образом

Отсюда

(s.16)

Установим действие оператора на функцию . Так как

то

В результате получаем

(s.17)

Перейдем к определению явного вида волновых функций стационарных состояний квантового гармонического осциллятора. При этом воспользуемся свойствами (s16) и (s.17) операторов уничтожения и рождения. Для решения задачи необходимо в первую очередь определить волновую функцию , соответствующую наименьшему собственному значению Волновые функции для собственных значений можно определить, используя свойство (s.17) оператора рождения. Так как

то учитывая явный вид (s.4) для оператора уничтожения, получаем следующее дифференциальное уравнение первого порядка

(s.18)

Его решение имеет вид

(s.19)

Здесь учтено условие нормировки Остальные функции получаем, используя свойство (s.17) оператора рождения :

. (s.20)

Для определения результата действия й степени оператора рождения на волновую функцию основного состояния , рассмотрим следующее выражение. Имеем

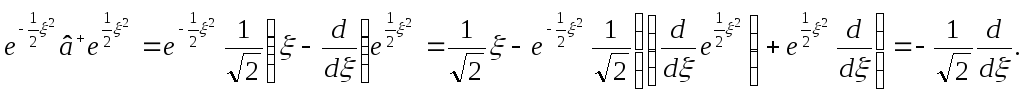
Перепишем выражение (s.20) в виде

Далее подставим в произведение операторов единичный оператор В результате, получим

Учитывая явный вид оператора , приходим к произведению операторов , т.е. к произведению операторов В результате выражение для волновой функции принимает вид

или, учитывая (s.19)

(s.21)

Окончательно, собственные функции оператора Гамильтона для квантового гармонического осциллятора можно представить в виде

(s.22)

где

(s.23)

Функции хорошо известны в математике и называются полиномами Чебышова-Эрмита. Эти функции образуют полный ортонормированный набор:

Окончательно, возвращаясь к размерной переменной решение спектральной задачи (s.2), имеет вид

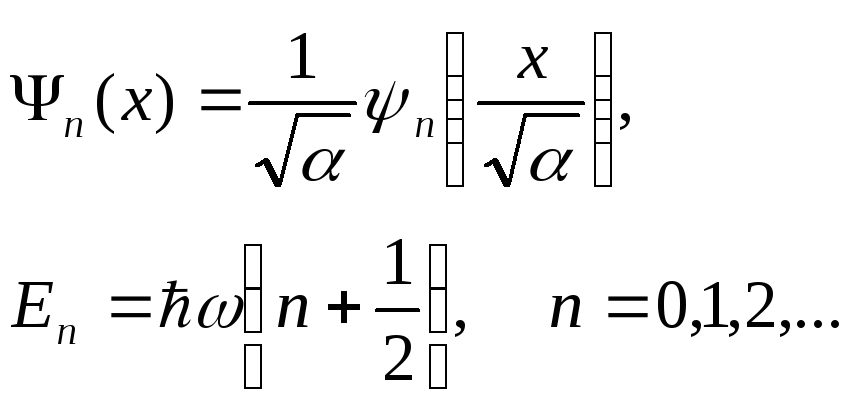(s.24)

Для вычисления различных средних физических величин, нам понадобятся рекуррентные соотношения для функций и формулы их дифференцирования по переменной Их легко вывести, если воспользоваться выражениями (s.16), (s.17) для операторов рождения и уничтожения. Учитывая их явный вид, получаем

(s.25)

(s.26)

Сравнение классического и квантового гармонических осцилляторов

1. Полная энергия классического гармонического осциллятора может принимать любые положительные значения, начиная с . При частица покоится в начале координат. В квантовом случае результат принципиально иной. Полная энергия может принимать только дискретные значения Спектр энергий эквидистантный - независит от . Наименьшее значение энергии называется энергией нулевых колебаний.

2. Средние значения координаты и импульса классического осциллятора равны нулю: Для квантового осциллятора среднее значение координаты и импульса соответственно равны:

Учитывая выражения (s.25), (s.26) находим

Здесь учтено, что функции образуют полный ортонормированный набор, так, что

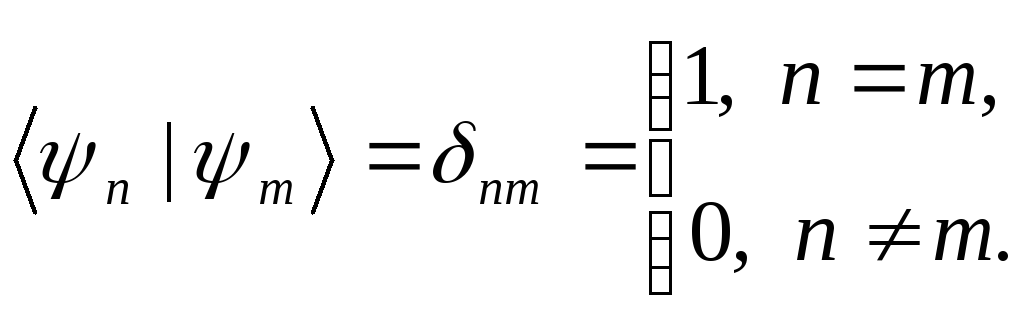
Таким образом, и для классического и квантового осциллятора средние значения координат и импульса равны нулю.

3. Для модели классического гармонического осциллятора его энергия связана со среднеквадратичным отклонением от положения равновесия выражением

где черта сверху означает среднее по периоду колебаний Проверим выполняется ли подобное соотношение в квантовом случае. Для этого вычислим, используя формулы (s.25), (s.26), среднеквадратичные флуктуации координаты в произвольном состоянии . Имеем

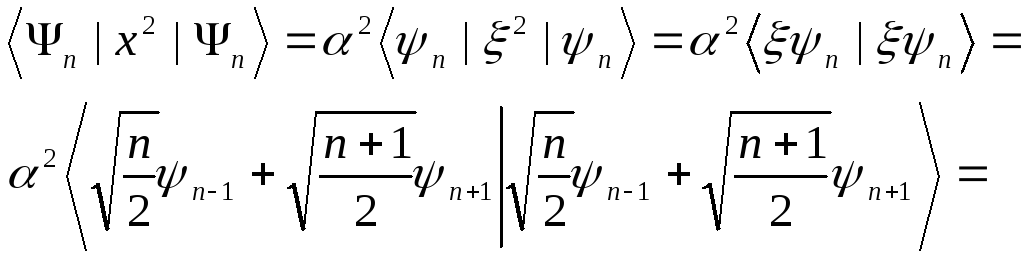
С учетом выражения для спектра энергии в (s.24), получаем

Таким образом, и в классическом и квантовом случаях, связь между энергией и среднеквадратичными отклонениями от положения равновесия одинакова.

4. Для классического осциллятора имеет место теорема вириала: , где - средняя по периоду колебаний кинетическая энергия частицы. Какова связь между средней кинетической и потенциальной энергиями осциллятора в произвольном квантовом состоянии ? Рассмотрим среднее

.

Отсюда, непосредственно, следует

Таким образом, и в квантовом случае средняя кинетическая энергия равна средней потенциальной энергии, т.е. теорема вириала выполняется.

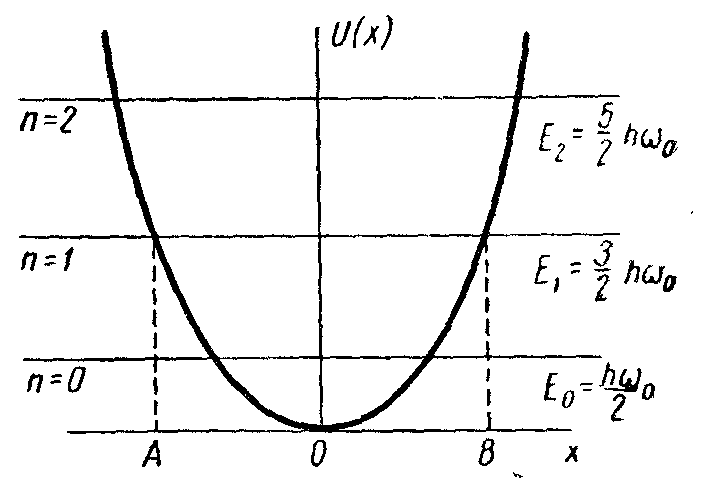
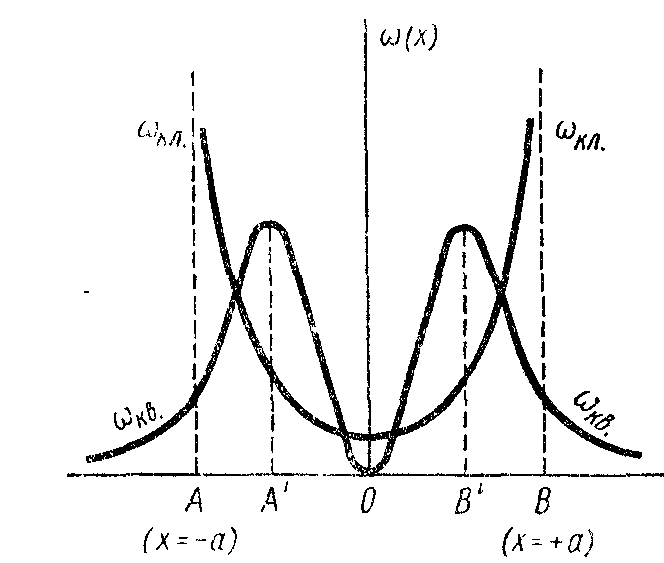
5.1. Обсудим некоторые особенности квантовых состояний гармонического осциллятора. На рис. представлена диаграмма квантовых уровней и потенциальной энергии . Для примера рассмотрим квантовый уровень с энергией В классическом случае частица с такой энергией может совершать колебательные движения между точками и (точками поворота, где кинетическая энергия обращается в ноль). Обозначим амплитуду колебаний через и определим вероятность нахождения частицы в области , лежащей внутри отрезка .

Эта вероятность равна

где время, за которое частица проходит расстояние а период колебаний. Пусть период колебаний равен тогда

где - скорость частицы. Выразим скорость частицы через переменную Для простоты положим, что решение уравнения движения для классического осциллятора имеет вид Отсюда

Таким образом, искомая вероятность равна

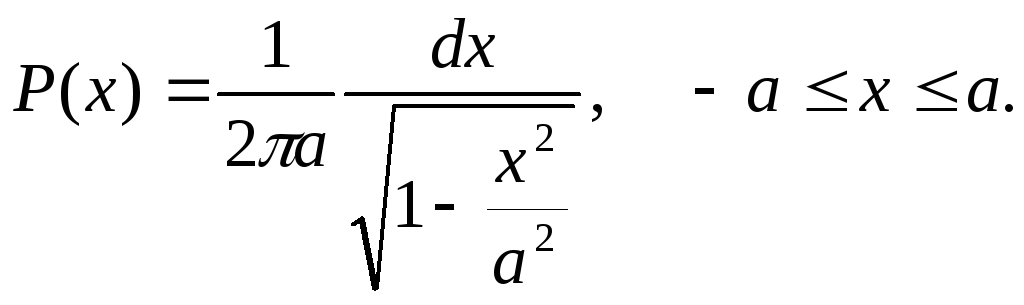(s.27)

Выражение, стоящее перед представляет собой, очевидно, плотность вероятности. Обозначим ее как

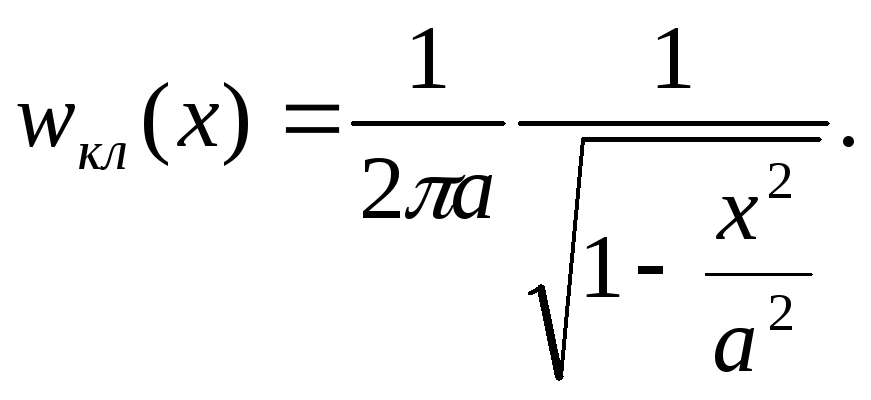(s.28)

Заметим, что для распределения (s.28) условие нормировки выполняется. Из вида распределения (s.28) видно, что функция имеет минимум в точке , в точках поворота Таким образом, вероятность встретить частицу в центральной области мала из-за того, что здесь скорость частицы максимальна, в окрестности точек поворота скорость мала и вероятность встретить частицу больше.

Рассмотрим квантовый гармонический осциллятор. Вероятность найти частицу в области в произвольном квантовом состоянии равна

(s.29)

В состоянии с энергией

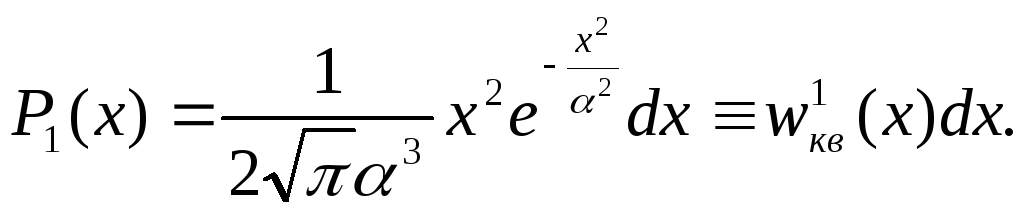(s.30)

Распределение 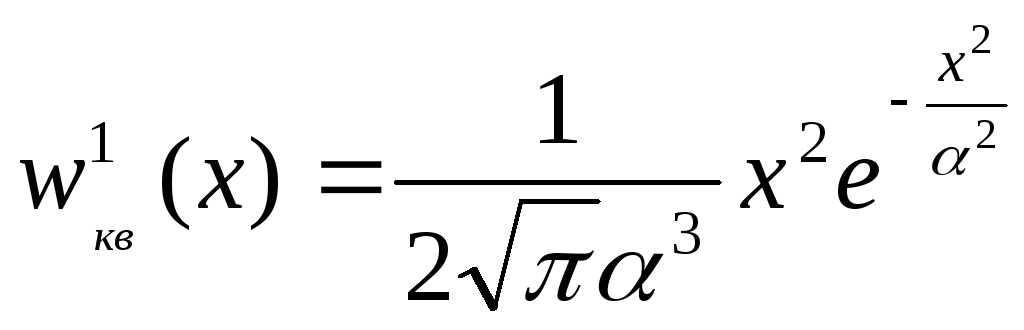имеет три точки экстремума - точка минимума и две точки максимума (точки и соответственно). Для уровня точки поворота и имеют координаты Важно, что распределение определено и за пределами точек поворота, т.е. имеется отличная от нуля вероятность найти частицу вне области