
- •Министерство образования и науки
- •Правила выполнения контрольной работы
- •Варианты контрольных работ
- •Образцы решения типовых заданий.
- •Контрольная работа №2.
- •Контрольные работы для студентов со средним профессиональным образованием (спо).
- •Перечень контрольных вопросов к экзамену по курсу «Математический анализ»
- •Список литературы:
Варианты контрольных работ
Чтобы определить номер своего варианта, студент должен воспользоваться приведённой ниже таблицей. Например, если номер студента в учебном журнале - первый, то он выполняет задание для варианта № 1, если двенадцатый- то вариант № 2, если тринадцатый -то вариант № 3 и т. д. Затем, определив номер своего варианта, необходимо из каждого задания контрольной работы выбрать задачу с соответствующим номером.
|
Вариант, присвоенный студенту учебным отделом |
Вариант контрольной работы |
|
1, 11, 21 |
1 |
|
2, 12, 22 |
2 |
|
3, 13, 33 |
3 |
|
4, 14, 24 |
4 |
|
5,15, 25 |
5 |
|
6, 16, 26 |
6 |
|
7,17, 27 |
7 |
|
8, 18, 28 |
8 |
|
9, 19,29 |
9 |
|
10, 20, 30 |
10 |
Образцы решения типовых заданий.
ПРИМЕР 1. Найдите предел![]()
Решение.
Разделим числитель и знаменатель выражения на 7n. После преобразований получим:
![]()
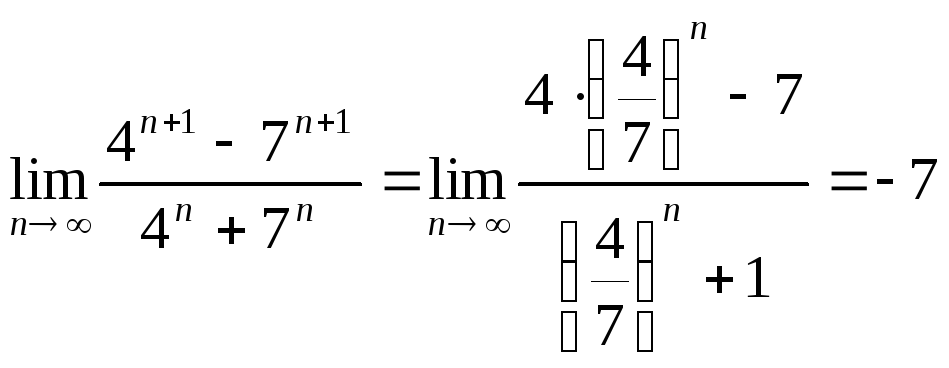 .
.
(Так как при
![]() выражение
выражение![]() стремится к нулю по свойству показательной
функции с основанием 0<a<1).
стремится к нулю по свойству показательной
функции с основанием 0<a<1).
ПРИМЕР 2. Найдите предел
![]()
Решение.
Имеем неопределённость вида
![]() .
Чтобы устранить её, разделим числитель
и знаменатель на
.
Чтобы устранить её, разделим числитель
и знаменатель на![]() :
:
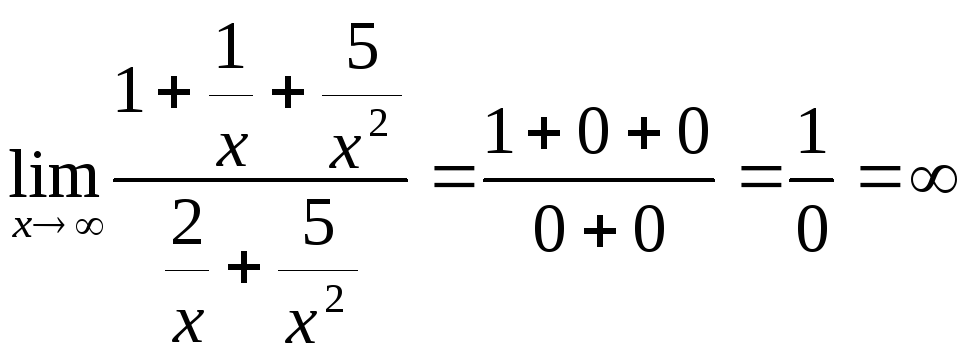 .
.
ПРИМЕР 3. Найдите предел
![]() .
.
Решение.
Имеем неопределённость вида
![]() .
Чтобы раскрыть её, умножим и разделим
выражение в скобках на сопряженное ему
выражение
.
Чтобы раскрыть её, умножим и разделим
выражение в скобках на сопряженное ему
выражение![]() .
Получим:
.
Получим:
![]() .
.
ПРИМЕР 4. Найти предел
![]()
Решение.
Имеем неопределенность вида “0/0”. Подвергнем функцию преобразованию, чтобы получить возможность использовать первый замечательный предел;
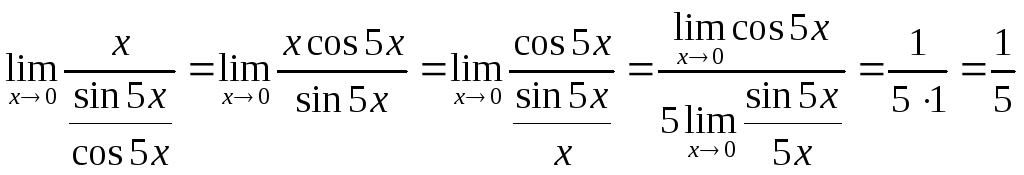 .
.
ПРИМЕР 5. Найти предел![]() .
.
х
Решение.
Имеем неопределённость вида
![]() .
Чтобы воспользоваться вторым замечательным
пределом, преобразуем данную функцию:
.
Чтобы воспользоваться вторым замечательным
пределом, преобразуем данную функцию:
![]() .
.
ПРИМЕР 6. Продифференцировать функцию:
![]() .
.
Решение.
Находим производную данной функции по правилам дифференцирования сложной функции:
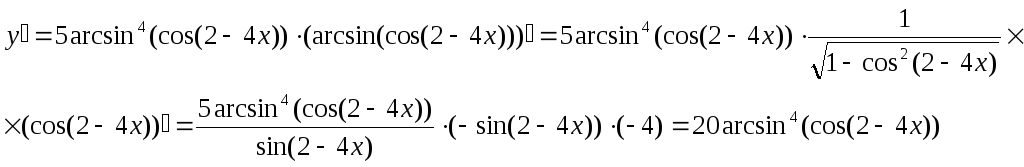 .
.
ПРИМЕР 7. Найти производную функции,
заданной неявно:
![]() .
.
Решение.
Дифференцируем данную функцию по х:
![]() ,
откуда
,
откуда![]()
ПРИМЕР 8. Найти производную
![]() от функции, заданной параметрически:
от функции, заданной параметрически:![]() .
.
Решение.
![]() .
.
ПРИМЕР 9. Найти область определения
функции
![]()
Решение.
Данная функция определена для всех х,
не обращающих в нуль знаменатель, т.е.
не являющихся корнями уравнения![]() .
Это все числа вида
.
Это все числа вида![]() .
.
Таким образом, область определения
D(у) - вся числовая
прямая, кроме точек![]() .
.
ПРИМЕР 10. Исследовать функцию и построить
ее график:
![]()
Решение.
Функция определена и непрерывна в
интервале (0;+). В
граничной точке![]() области определения функция имеет
бесконечный разрыв, так как
области определения функция имеет
бесконечный разрыв, так как![]() .
.
Так как в точке
![]() функция имеет бесконечный разрыв, то
прямая
функция имеет бесконечный разрыв, то
прямая![]() является вертикальной асимптотой.
Найдем уравнение наклонной асимптоты
является вертикальной асимптотой.
Найдем уравнение наклонной асимптоты![]() (если
она существует).
(если
она существует).
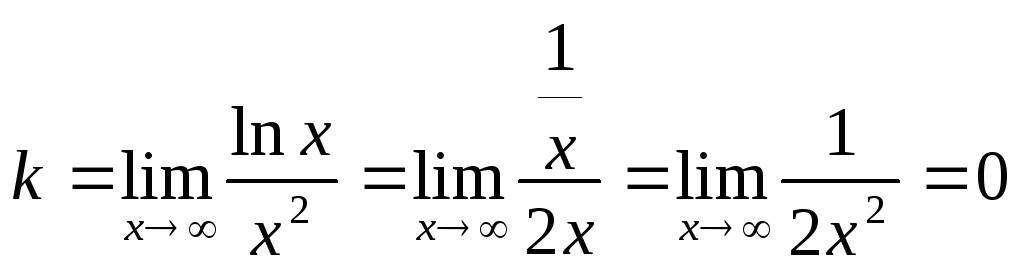 ;
;
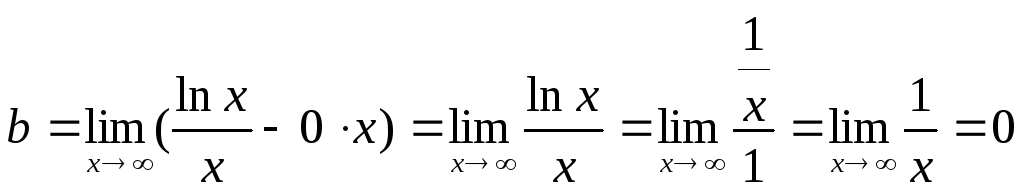 .
.
(При нахождении пределов воспользовались правилом Лопиталя).
Итак,
![]() и уравнение асимптоты
и уравнение асимптоты![]() .
Таким образом, график имеет в качестве
асимптот оси координат.
.
Таким образом, график имеет в качестве
асимптот оси координат.
Найдем производную функции и критические точки:
![]() .
Стационарная критическая точка:
.
Стационарная критическая точка:![]() .
Исследуем знак производной на
интервалах(0;е) и (е;).
.
Исследуем знак производной на
интервалах(0;е) и (е;).
х
0 е

+ -
Составим таблицу:
x (0;e) e (e;+) y` + 0 - y возрастает max убывает
Экстремум функции:
![]() .
.
Найдем вторую производную и значения х, при которых график может иметь точку перегиба:
![]() ,
,![]() при
при![]() .
.
Определим знак второй производной в
интервалах
+ -![]() и
и![]() :
:

-
х
0 +
![]()
x (0; ( y`` - 0 + график выпуклый точка
перегиба вогнутый
![]() )
)
![]() 4,48
4,48
![]() ;)
;)
Составим таблицу:
y(![]() )=3/(
)=3/(![]() )0.33
)0.33
График пересекает ось абсцисс в точке (1;0). Точек пересечения с осью ординат нет. Строим эскиз графика функции:
у
х
1 е


![]() е
е
ПРИМЕР 11. Построить график функции, заданной уравнением в полярных координатах
![]()
Решение.
Построим график данной функции в
декартовых координатах для
![]() :
:
r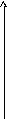

/2
3/2 2
![]()
φ
0
Из этого графика видно, что
![]() при
при![]() имеем
имеем![]() .
.
Поэтому требуемый график будет находиться
в секторах, соответствующих данным
значениям , а также
в секторах, симметричных им относительно
начала координат (в силу того, что перед![]() стоит чётный коэффициент).
стоит чётный коэффициент).
Учитывая характер изменения rв этих промежутках (от 0 до 1 и затем снова до 0) получим следующий график (восьмилепестковую розу):
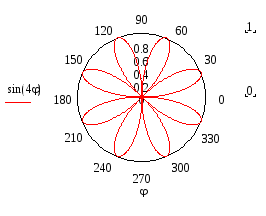
ПРИМЕР 12. Исследовать сходимость ряда
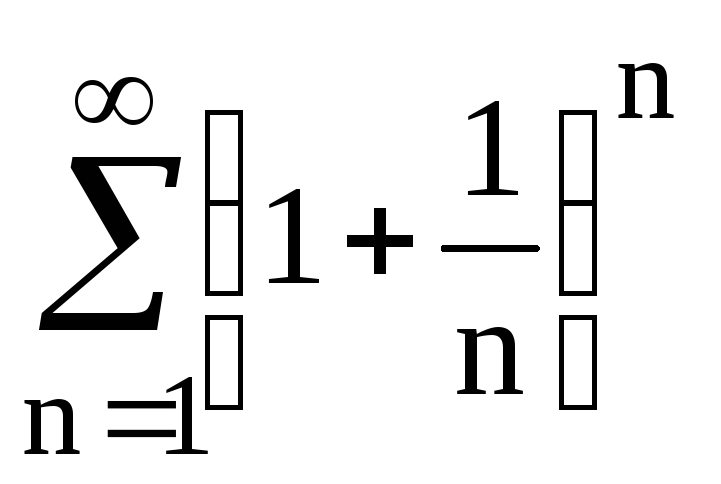
Проверим, выполняется ли необходимое условие сходимости знакоположительного ряда. Найдём предел общего члена ряда
![]() .
.
Так как данный предел не равен нулю, то не выполняется необходимое условие сходимости ряда, следовательно, он расходится.
ПРИМЕР 13. Разложить функцию
![]() в ряд по степеням х.
в ряд по степеням х.
Решение.
Разложим функцию в ряд Маклорена.
Учитывая, что
![]() ,
разложим функцию на сумму двух более
простых:
,
разложим функцию на сумму двух более
простых:
![]() .
.
Далее преобразуем:
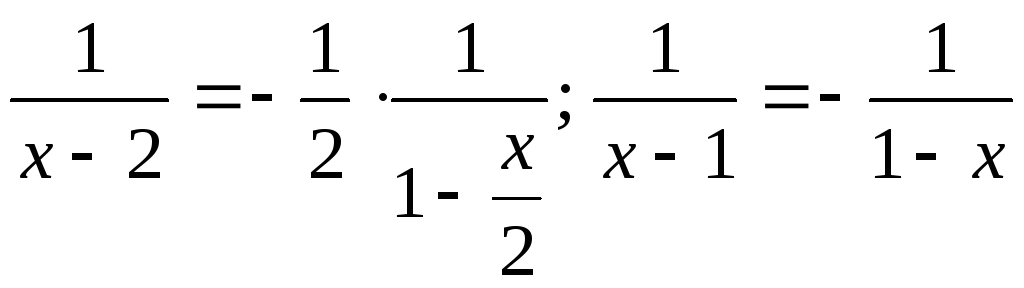 .
.
Воспользуемся разложением:
![]() .
.
*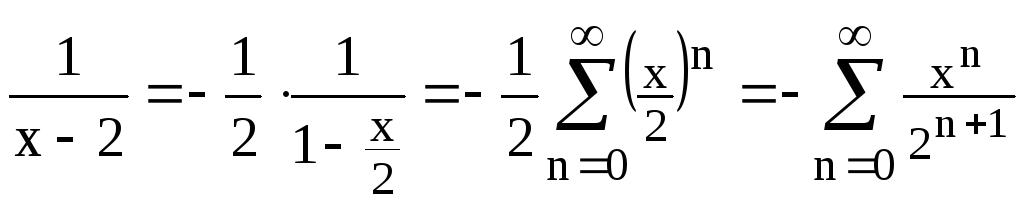 (при
(при![]() <1, т.е. при
<1, т.е. при![]() <2)
<2)
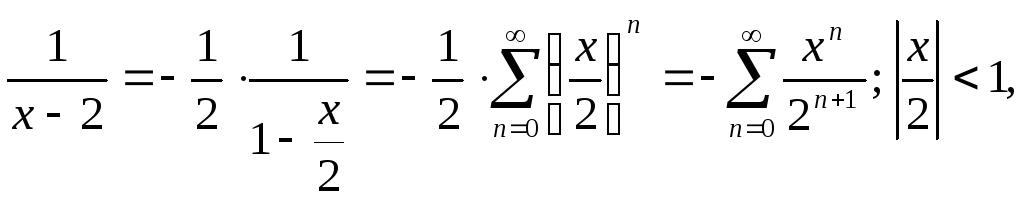 то есть
то есть![]() .
.
Аналогично получим второе разложение:
![]() .
.
Тогда:
![]() .
.
Окончательно получаем:
![]()
ПРИМЕР 14. Найти неопределённый интеграл
![]() .
.
Решение.
Введем подстановку
![]() ,
откуда
,
откуда![]() .
Тогда
.
Тогда![]() .
Находим полученный табличный интеграл
и возвращаемся к прежней переменной:
.
Находим полученный табличный интеграл
и возвращаемся к прежней переменной:
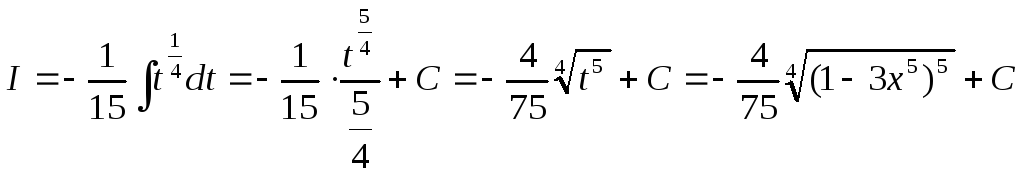 .
.
ПРИМЕР 15. Найти неопределённый интеграл
![]() .
.
Решение.
Подведем под знак дифференциала знаменатель подынтегральной дроби:
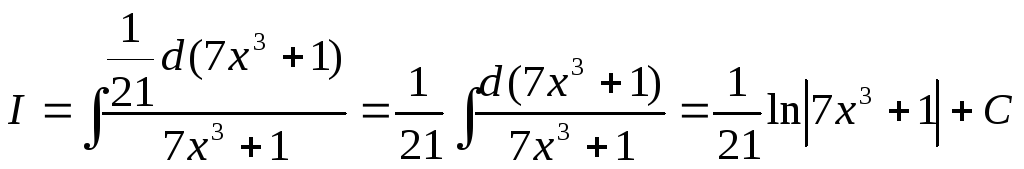 .
.
ПРИМЕР 16. Найти неопределённый интеграл
![]() .
.
Решение.
Применим формулу интегрирования по
частям:
![]() .
В данном случае:
.
В данном случае:
![]() .
Подставляя эти выражения в формулу,
получим:
.
Подставляя эти выражения в формулу,
получим:
![]() .
.
ПРИМЕР 17. Вычислить интеграл 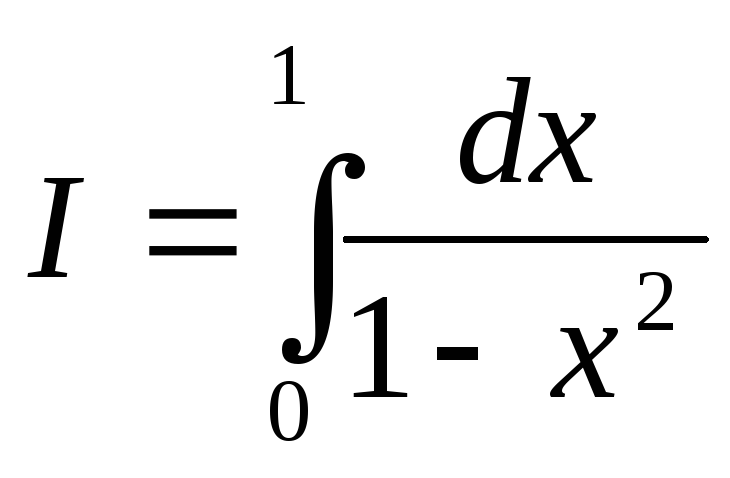 или установить его расходимость.
или установить его расходимость.
Решение.
Точка ![]() является особой точкой, поскольку
подынтегральная функция имеет в ней
бесконечный разрыв. Поэтому:
является особой точкой, поскольку
подынтегральная функция имеет в ней
бесконечный разрыв. Поэтому:
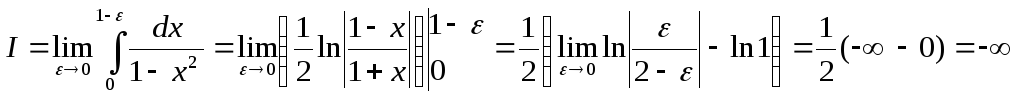 - получили бесконечный предел.
- получили бесконечный предел.
Таким образом, данный интеграл расходится.
ПРИМЕР 18. Решить уравнение: ![]() .
.
Решение.
Данное уравнение является дифференциальным уравнением первой степени с Разделяющимися переменными. Разделим переменные:
![]() .
.
Проинтегрируем части последнего равенства:
![]() .
.
Отсюда:
![]() .
.
Окончательно имеем:
![]() - общее решение данного уравнения.
- общее решение данного уравнения.
ПРИМЕР 19. Решить уравнение: ![]() .
.
Решение.
Данное дифференциальное уравнение относится к типу однородных дифференциальных уравнений
![]() ,
,
которые решаются с помощью подстановки
![]() .
.
Отсюда:
![]() .
.
После подстановки в исходное уравнение получим:
![]() .
.
Это – уравнение с разделяющимися переменными. Разделяем переменные:
![]()
Интегрируя обе части, получим:
![]()
Используя обратную подстановку, получим:
![]()
Окончательно имеем обще решение в виде:
![]() .
.
Теперь, чтобы найти частное решение, подставляем в общее решение начальное условие:
![]() .
.
Искомое частное решение:
![]() .
.
Контрольные работы для студентов со средним полным образованием.
Контрольная работа № 1.
Задание 1. Найти следующие пределы:
1a)![]() ;
б)
;
б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
2.a)
![]() ; б)
; б)![]() ;
;
в)
![]() г)
г)![]() ;
;
3. а)![]() ;
б)
;
б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
4.a)
![]()
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
5.a)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ; в)
; в)
![]() ;
;
6.a)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
7.a)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
8.a)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ; г)
; г)
![]()
9.a)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
10a)
![]() ;
б)
;
б)
![]() ;
;
в)![]() ;
г)
;
г)![]()
Задание 2.Найдите производные функций:
1.
а)y=extgx+![]() ;
б)x=ln(xy)
; в)
;
б)x=ln(xy)
; в)
![]()
a) y = ln(excosx + exsinx) ; б) x4+y4 = x2y2 ; в)
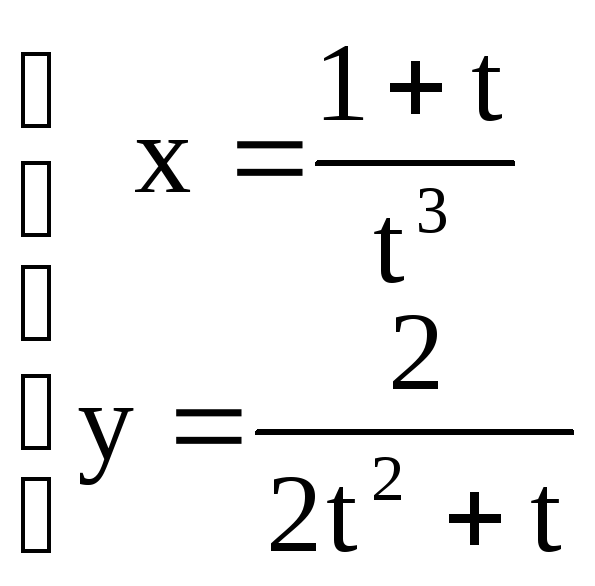
a) y = arcsin(sinx – cosx) ; б) x = ex+y ; в)
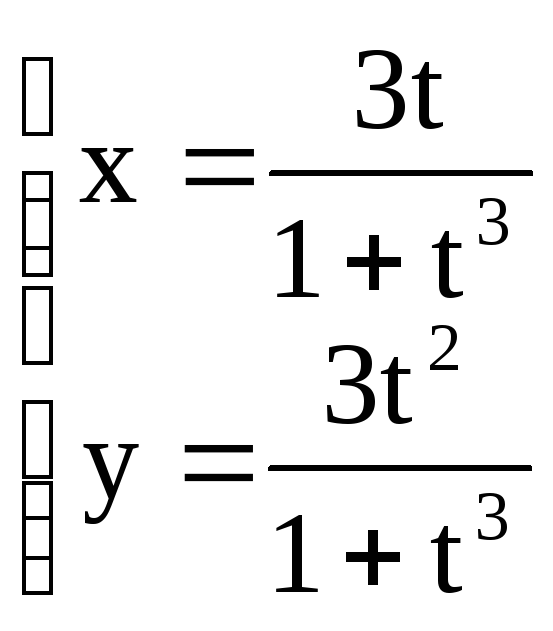
a) y = ln
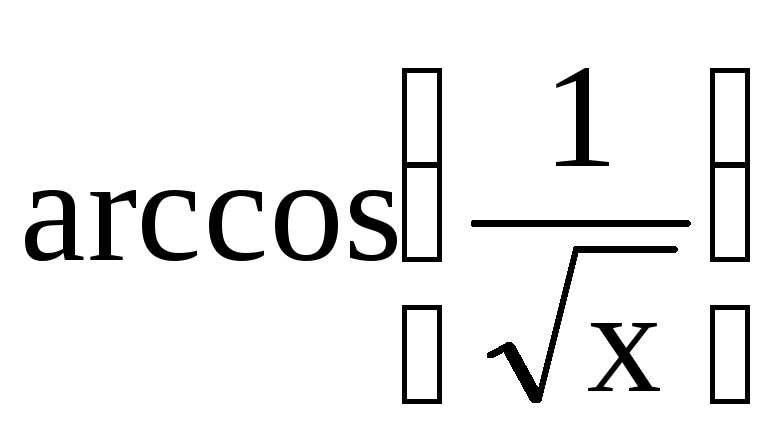 ;
б) cos(xy)=x ; в)
;
б) cos(xy)=x ; в)
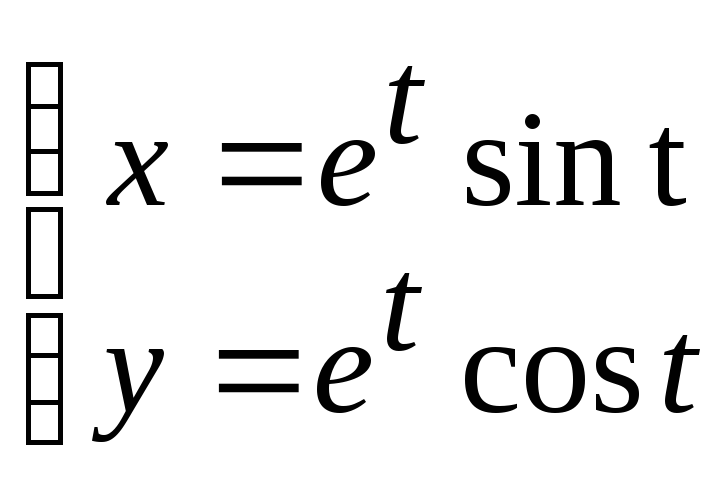
a) y = x2log3x+3x ; б) x3+y3-3xy=0 ; в)
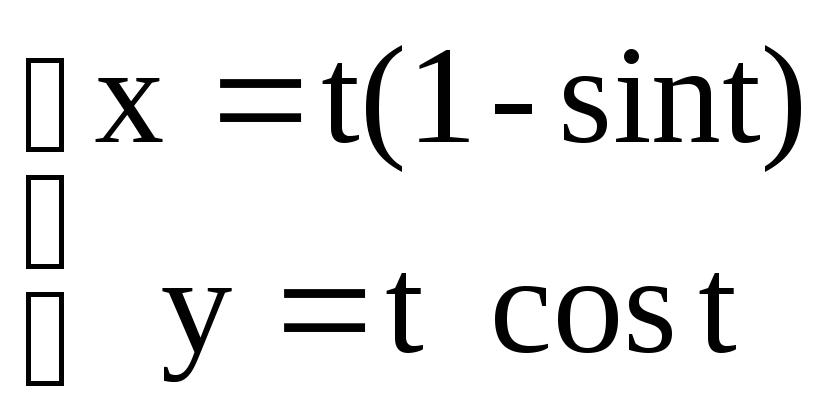
a) y =
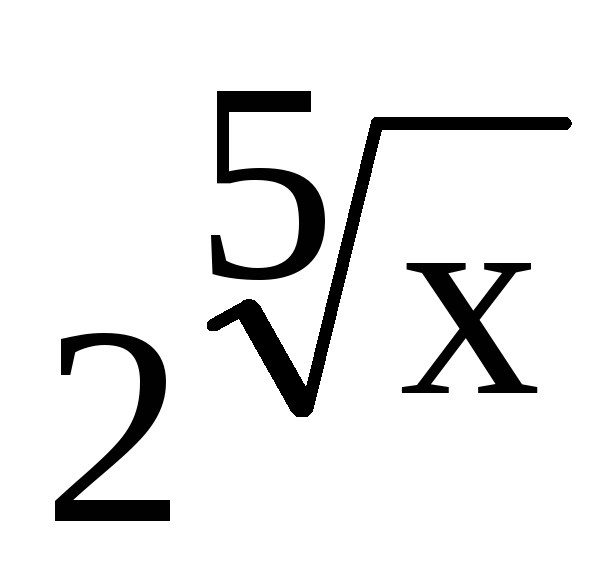 sin3x
; б)
sin3x
; б)
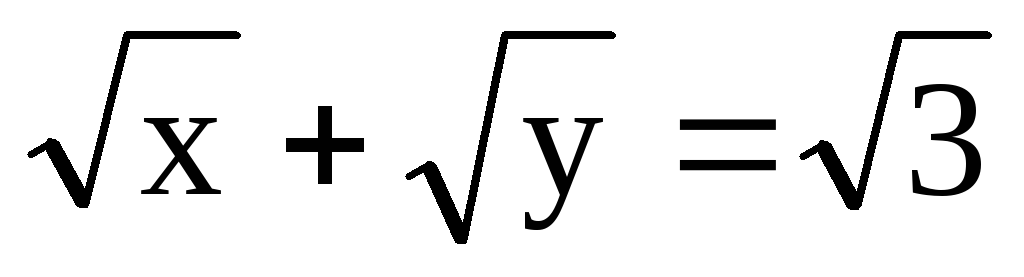 ;
в)
;
в)
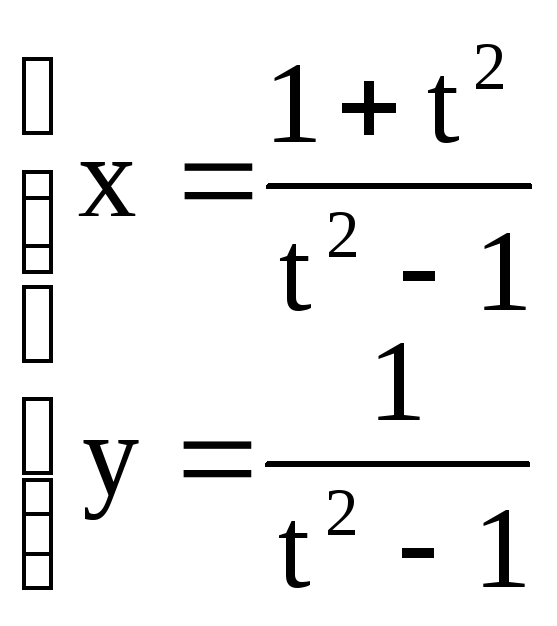
а) y=
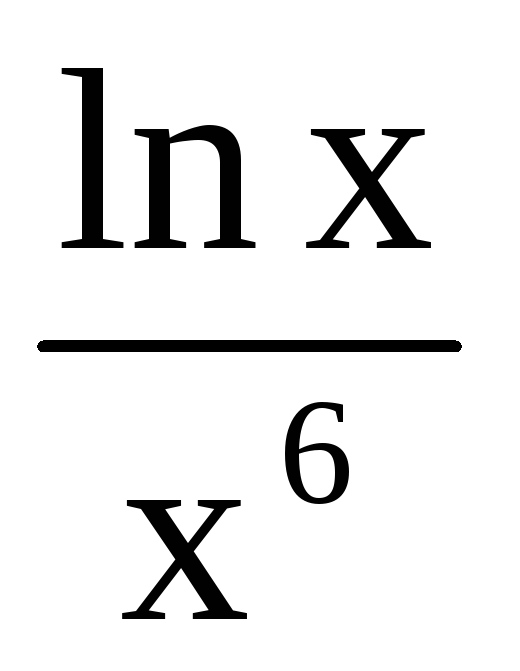 ;
б)yx=xy; в)
;
б)yx=xy; в)
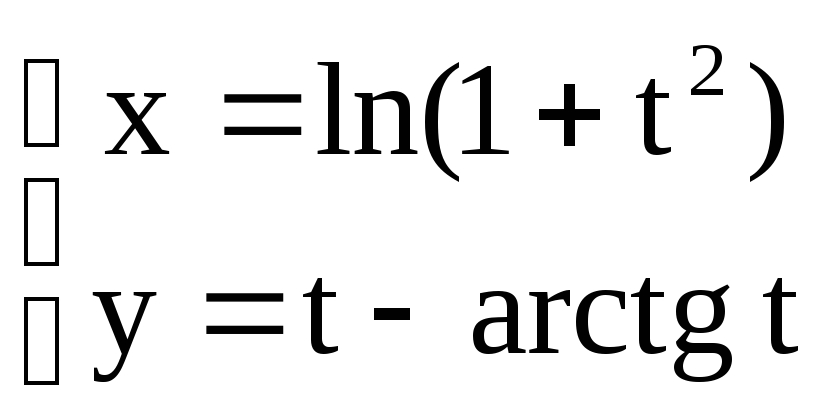
а) y=
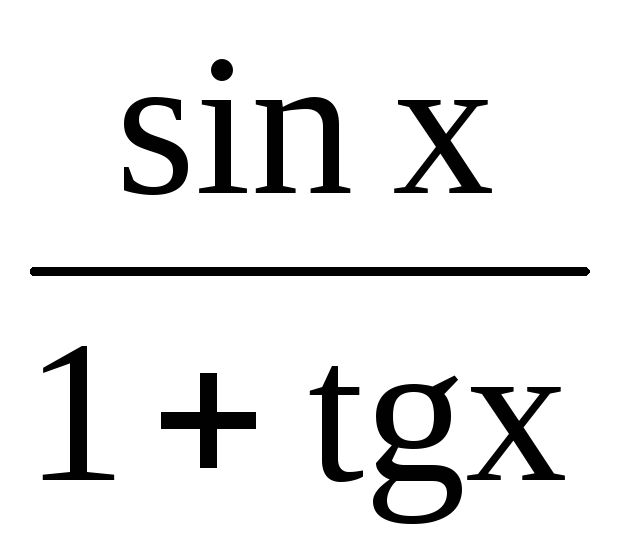 ; б)x3+y3-6xy=0
; в)
; б)x3+y3-6xy=0
; в)
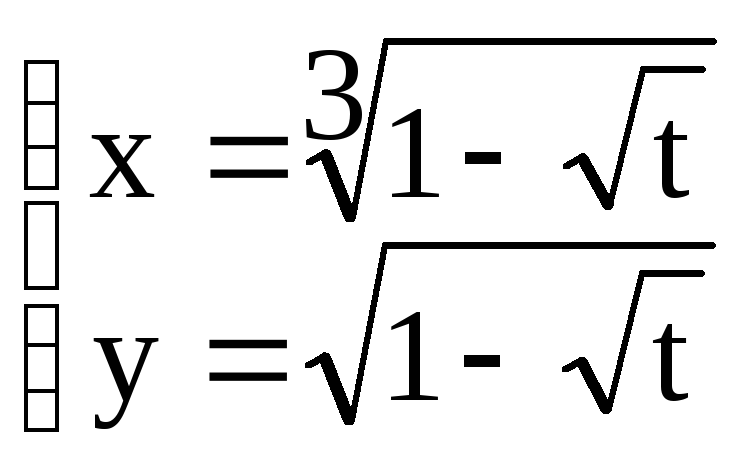
а) y=
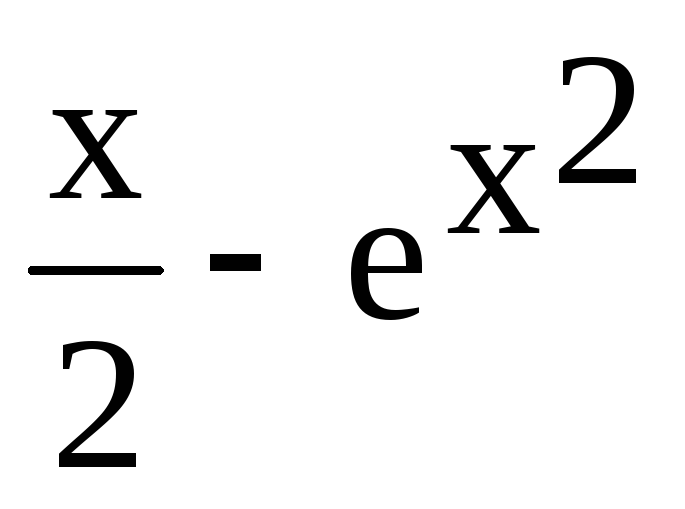 ; б)y=2x+arctgy; в)
; б)y=2x+arctgy; в)
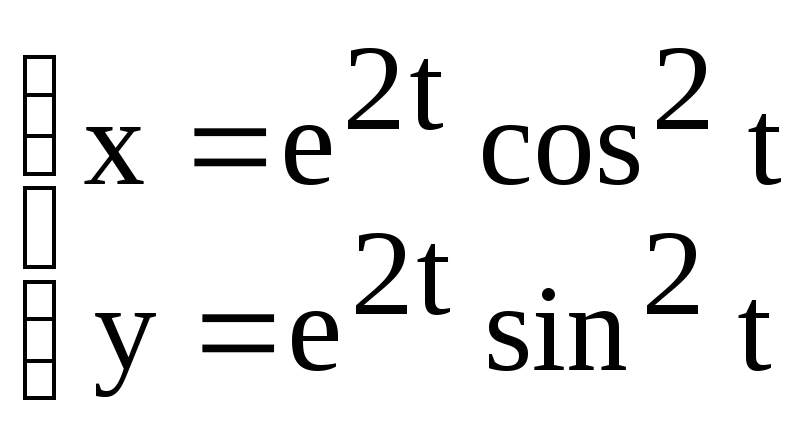
а) y=arctg
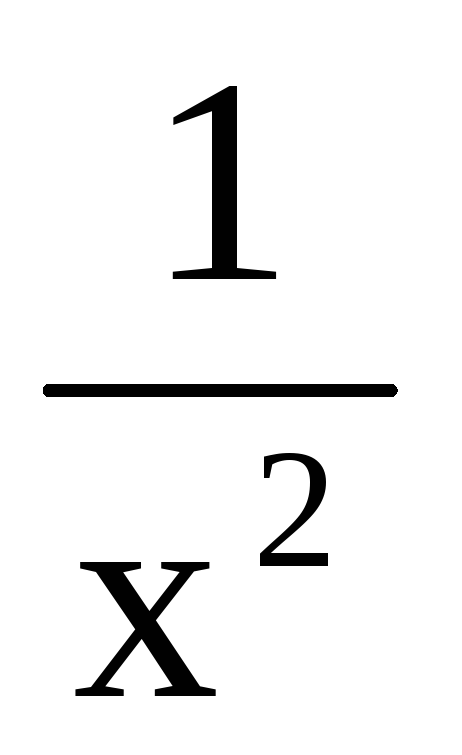 ;
б)x3+x2y+y2=0
; в)
;
б)x3+x2y+y2=0
; в)
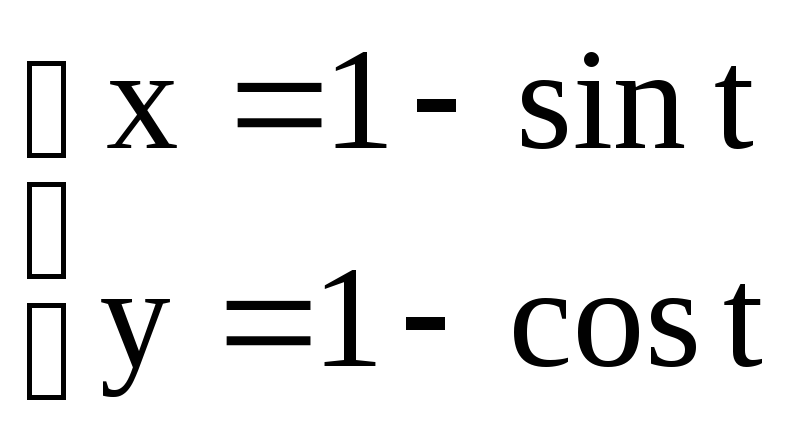
Задание 3. Найти область определения функций
1. y
=
![]() ;
2. y =
;
2. y =
![]() ;
3. y =
;
3. y =![]() ; 4. y =
; 4. y =
![]()
5.
y =![]() ;
6. y =
;
6. y =![]() ;
7. y =
;
7. y =![]() ;
8. y =
;
8. y =![]()
9.
y =
![]() ;
10. y =
;
10. y =![]()
Задание 4.Исследуйте функцию с помощью производной и постройте ее график:
1.
y = ln sin x;
2. y=log2![]() -x,
3. y=
-x,
3. y=![]() ; 4. y=cos3x,
5. y= ln(x2-1)
; 4. y=cos3x,
5. y= ln(x2-1)
6.
y=3![]() ,
7. y=
x3+
,
7. y=
x3+![]() ;
8. y=2
;
8. y=2![]() ; 9. y=
; 9. y=![]() (x-1)e3x+1
; 10. y=
(x-1)e3x+1
; 10. y=![]() ln
x
ln
x
Задание 5.Построить график функции, заданной уравнениями в полярных координатах.
1. r=sin4; 2. r=; 3. r=cos2; 4. r=ln ; 5. r=sin +1,
6. r=sin2; 7. r=2+sin; 8. r=cos ; 9. r=cos2-sin2; 10. r=sin3
