
1.1.3 Перевод чисел из одной системы счисления в другую
Задача перевода заключается в следующем. Пусть известна запись числа Х в системе счисления с каким либо основанием Р:
pn pn-1 … p1 p0 p-1 p-2 … , (1.6)
где pi - цифры Р-ичной системы (0 ≤ pi ≤ P-1). Требуется найти запись этого же числа X в ПСС с другим основанием Q:
qs qs-1 … q1 q0 q-1 q-2 …, (1.7)
где qi – искомые цифры Q-ичной ПСС (0 ≤ qi ≤ Q-1).
Можно ограничиться случаем положительных чисел, так как перевод отрицательного числа сводится к переводу его модуля и приписыванием к нему знака минус. Рассмотрим три способа перевода числа из одной ПСС в другую.
Первый способ. Согласно (1.6) можно записать:
 . (1.8)
. (1.8)
Для получения Q-ичного изображения (1.8) необходимо все цифры pi и число Р заменить Q- ичными изображениями и выполнить арифметические операции в Q- ичной ПСС. Как правило, этот способ применяют для преобразования в десятичную ПСС, хотя принципиально он применим для любых ПСС.
Пример 1. Перевести число х = 3718 в десятичную ПСС. Согласно изложенному правилу
![]() .
.
Пример
2. Перевести
число
![]() в десятичную ПСС. Действуя аналогично
первому примеру, получим:
в десятичную ПСС. Действуя аналогично
первому примеру, получим:
 .
.
Второй способ. Так как для перевода любого числа достаточно уметь переводить его целую и дробную части, то рассмотрим отдельно эти два случая.
Перевод целых чисел. Известна запись целого числа N в Р-ичной ПСС. Согласно (1.4) запись этого числа в Q-ичной ПСС будет иметь вид:
![]() (1.9)
(1.9)
где
![]() .
Для определения q0
разделим
обе части (1.9) на Q,
причём в левой части произведём деление,
пользуясь правилами Р-ичной
арифметики, и получим:
.
Для определения q0
разделим
обе части (1.9) на Q,
причём в левой части произведём деление,
пользуясь правилами Р-ичной
арифметики, и получим:
![]() , (1.10)
, (1.10)
![]() .
(1.11)
.
(1.11)
В (1.10) скобками указана операция целочисленного деления, а в (1.11) записана операция взятия остатка от деления N нацело на Q. Теперь, для определения q1, к N1 можно применить те же операции:
 .
.
Таким
образом, пологая
![]() ,
перевод чисел с использованием P-ичной
арифметики осуществляется по следующим
рекуррентным формулам:
,
перевод чисел с использованием P-ичной
арифметики осуществляется по следующим
рекуррентным формулам:
 . (1.12)
. (1.12)
Этот
процесс продолжается до тех пор, пока
не будет получено
![]() .
Заметим, что поскольку операции
выполняются в Р-ичной
ПСС, то в этой же ПСС будут получены
искомые коэффициенты
.
Заметим, что поскольку операции
выполняются в Р-ичной
ПСС, то в этой же ПСС будут получены
искомые коэффициенты
![]() , поэтому
каждый из них необходимо записать одной
Q-ичной
цифрой.
, поэтому
каждый из них необходимо записать одной
Q-ичной
цифрой.
Замечание. Рекуррентная формула – это соотношение вида:
![]()
которое
позволяет вычислить все члены
последовательности
![]() ,
если заданы её первые р
членов и вид функционального отображения
f(∙).
,
если заданы её первые р
членов и вид функционального отображения
f(∙).
Пример 1. Перевести число N = 47 в двоичную ПСС. Применяя формулы (1.12), имеем:
47 : 2 = 23(1)
23 : 2 = 11(1)
11 : 2 = 5(1)
5 : 2 = 2(1)
2 : 2 = 1(0)
1 : 2 = 0(1)
Здесь
в скобках указывается остаток
от деления нацело.
Поскольку числа 0 и 1 в обеих ПСС (десятичной
и двоичной) обозначаются одинаковыми
цифрами, то переводить остатки в двоичную
ПСС не требуется. Следовательно, записывая
остатки в обратном порядке, имеем
результат
![]() .
.
Пример 2. Перевести число N = 3060 в шестнадцатеричную систему. Применяя формулы (1.12) при Q = 16, получим:
3060 : 16 = 191(4)
191 : 16 = 11(15)
11 : 16 = 0(11).
Отсюда: q0 = 4, q1 = 1510 = f, q2 = 11 = b , то есть N =bf416 .
2. Перевод дробных чисел. Пусть необходимо перевести в Q-ичную ПСС правильную дробь х (0<x<1), заданную в Р-ичной ПСС. Так как х < 1, то число x в Q-ичной ПСС можно представить в виде:
![]() ,
(1.13)
,
(1.13)
где
![]() (i=1,2,…)
– искомые коэффициенты Q-ичного
разложения числа х.
Умножим обе части (1.13) на Q,
причём в левой части равенства умножение
выполним в Р-ичной
ПСС. Тогда:
(i=1,2,…)
– искомые коэффициенты Q-ичного
разложения числа х.
Умножим обе части (1.13) на Q,
причём в левой части равенства умножение
выполним в Р-ичной
ПСС. Тогда:
![]() .
(1.14)
.
(1.14)
Учитывая,
что
![]() и выделяя целую и дробную часть выражения
(1.14), получим:
и выделяя целую и дробную часть выражения
(1.14), получим:

Символом
D(∙)
– мы обозначили операцию взятия дробной
части числа. Ясно, что
![]() также будет правильной дробью, к которой
можно применить аналогичную операцию.
Таким образом, процесс вычисления
величин
также будет правильной дробью, к которой
можно применить аналогичную операцию.
Таким образом, процесс вычисления
величин
![]() можно записать в виде рекуррентных
формул (полагая
можно записать в виде рекуррентных
формул (полагая
![]() ):
):
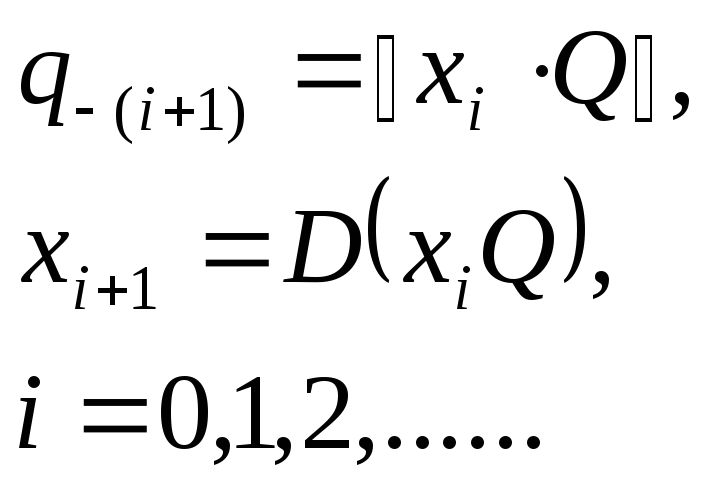 (1.15)
(1.15)
Это
процесс продолжается до тех пор, пока
не будет получено
![]() ,
или не будет достигнута требуемая
точность изображения числа. Её следует
определять из следующих соображений.
Пусть единица младшего разряда числа
х,
заданного в Р-ичной
ПСС, есть
,
или не будет достигнута требуемая
точность изображения числа. Её следует
определять из следующих соображений.
Пусть единица младшего разряда числа
х,
заданного в Р-ичной
ПСС, есть
![]() .
Тогда в Q-ичной
записи этого числа х
следует
сохранить l
разрядов
после точкой, где l
удовлетворяет условию:
.
Тогда в Q-ичной
записи этого числа х
следует
сохранить l
разрядов
после точкой, где l
удовлетворяет условию:
 . (1.16)
. (1.16)
Последняя цифра округляется по известным правилам.
Пример 1. Перевести число х = 0.2 в двоичную ПСС. Для начала оценим количества двоичных разрядов, которые необходимо оставить после десятичной точки. С этой целью исходя из соотношений (1.16) запишем неравенство
 .
.
Этому неравенству удовлетворяет l = 4, так как 1/16 > 1/20 > 1/32. Следовательно, в двоичном представлении этого числа необходимо оставить четыре двоичных разрядов после десятичной точки, но с целью правильного округления необходимо будет вычислить пять двоичных разрядов. Теперь, применяя последовательно формулы (1.15), получим:
0.2 ∙ 2 = 0 + 0.4 => q-1 = 0
0.4 ∙ 2 = 0 + 0.8 => q- 2 = 0
0.8 ∙ 2 = 1 + 0.6 => q-3 = 1
0.6 ∙ 2 = 1 + 0.2 => q-3 = 1
0.2 ∙ 2 = 0 + 0.4 => q-3 = 0 и здесь можно остановиться.
Таким образом, представлением точного числа 0.210 в двоичной ПСС является двоичная дробь (с учётом округления четвёртого двоичного разряда):
0.210 ≈ 0.00112 .
Пример 2. Преобразовать десятичное число 0.543 к шестнадцатеричному виду. Сразу оценим количество шестнадцатеричных разрядов, чтобы получить требуемую точность изображения числа в шестнадцатеричной ПСС. Запишем неравенства (1.16) для нашего случая:
 .
.
Подставляя сюда последовательно значения l, убедимся, что l =2 удовлетворяет этим соотношениям (1/256 > 1/2000 > 1/4096). Следовательно, с учётом округления необходимо вычислить три шестнадцатеричных разряда. Действуя по формулам (1.15), получим:
0.543∙16 = 8 + 0.688 => q-1 = 8
0.688∙16 = 11+ 0.008 => q-2 = 11
0.008∙16 = 0 + 0.128 => q-3 = 0 .
В итоге имеем: 0.54310 ≈ 0.8b .
Заметим, что иногда, учитывая представление дробей в виде (1.13), можно некоторые рациональные дроби легко преобразовать в двоичную дробь. Например, дробь вида 7/16 можно представить в виде 7∙2-4 = 1112∙2-4 =
= 0.01112 .
Третий
способ. Пусть
выполняется соотношение
![]() ,
где к
- целое положительное число и Q
< P.
Тогда для
перевода изображения числа х
из Р-ичной
ПСС в Q-ичную
достаточно каждую цифру Р-ичного
представления числа х
заменить на к
цифр Q-ичного
изображения этого числа, двигаясь вправо
и влево от десятичной точки. Недостающие
разряда представления числа дополняются
нулями. Например, дано число а7.с16
.
Требуется
получить его двоичное представление.
Согласно изложенному выше правилу
имеем, что P=16,
Q=2
и, следовательно,
,
где к
- целое положительное число и Q
< P.
Тогда для
перевода изображения числа х
из Р-ичной
ПСС в Q-ичную
достаточно каждую цифру Р-ичного
представления числа х
заменить на к
цифр Q-ичного
изображения этого числа, двигаясь вправо
и влево от десятичной точки. Недостающие
разряда представления числа дополняются
нулями. Например, дано число а7.с16
.
Требуется
получить его двоичное представление.
Согласно изложенному выше правилу
имеем, что P=16,
Q=2
и, следовательно,
16 = 24 .
Так как величина k =4, то необходимо каждую шестнадцатеричную цифру числа заменить на четыре цифры двоичной ПСС и получим:
а7.с16 6= 1010 0111. 11002.
В случае обратного преобразования (из Q-ичной ПСС в Р- ичную) действуют следующим образом: в исходной Q-ичной записи числа объединяются разряды в группы по к цифр, двигаясь влево и вправо от точки, отделяющей целую и дробные части. При этом, в случае необходимости, добавляют левее самой старшей или правее самой младшей значащей цифры соответствующее количество нулей. После этого, каждая такая группа записывается одной цифрой в Р-ичной ПСС.
Например, двоичное число 101 110. 12 можно записать в различных ПСС в таком виде:
10 11 10. 102 = 232.24, к = 2;
101 110. 1002 = 56.48, к = 3;
0010 1110. 10002 = 2е.816, к = 4.
