Глава 1.3 логические элементы.
Булева алгебра, как было описано выше, содержит три основных логических операции И, ИЛИ, НЕ. Если мы располагаем элементарными схемами, поведение которых по "входам и выходам" соответствует этим трем операциям, то соединив их между собой в соответствии с заданным булевым выражением, получим логическую схему, реализующую это выражение. Такие элементарные схемы существуют и называются ЛОГИЧЕСКИМИ ЭЛЕМЕНТАМИ или ВЕНТИЛЯМИ. Они должны работать в соответствии с алгоритмом, задаваемым таблицей истинности той или иной основной логической операции, и иметь сигналы на входах и выходах одинаковой физической природы. В принципе, схемы И, ИЛИ, НЕ могут быть электрическими, механическими, пневматическими и иными, важно лишь, чтобы 0 и 1 были идентичными как на входе, так и на выходе.
В современной вычислительной технике используется множество разнообразных логических устройств, которые могут выполняться в виде специализированных интегральных микросхем (ИМС). Однако внутри они выполняются в виде набора соединенных определенным образом вентилей. Такое построение не всегда экономично, поскольку специализированные ИМС предназначены для выполнения хотя и сложных, но всё же частных операций. Иногда проще и экономичнее использование универсальных базовых логических элементов (ЛЭ), которые, зачастую, подменяют собой строгое понятие логического элемента, данное выше.
Среди множества логических элементов можно выделить несколько групп, которые называют ФУНКЦИОНАЛЬНО ПОЛНЫМИ - это такие группы, с помощью логических элементов которых, реализуется любая логическая функция.
Функционально полными являются следующие пять групп логических элементов:
1. Y =
- отрицание, НЕ;
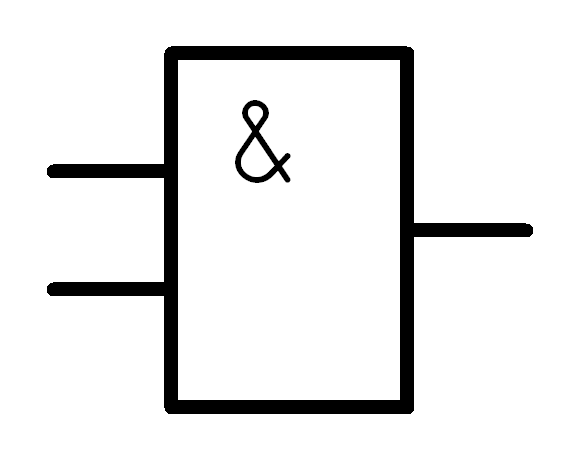
Y = X1 × Х2 - конъюнкция, И;
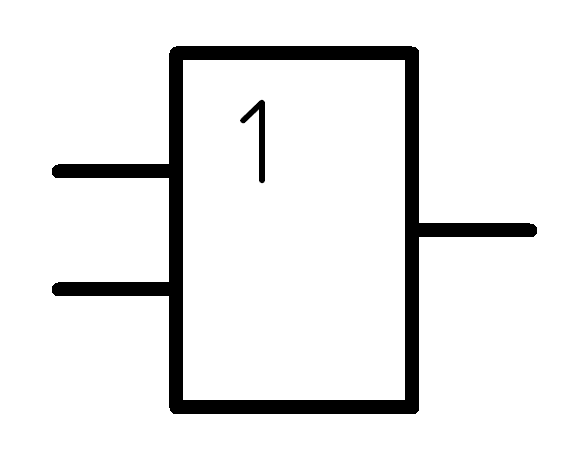
Y = X1 + Х2 - дизъюнкция, ИЛИ;
2. Y =
- отрицание, НЕ;
Y = X1 × Х2 - конъюнкция, И;
3. Y =
- отрицание, НЕ;
Y = X1 + Х2 - дизъюнкция, ИЛИ;
4. Y = 
- отрицание конъюнкции, И-НЕ (штрих
Шеффера);
5. Y =
- отрицание дизъюнкции, ИЛИ-HE (стрелка
Пирса).
Вентиль НЕ называют также ИНВЕРТОРОМ. Условные графические обозначения этих элементов в соответствии с ГОСТом приведены на рисунке 1.3.1. Условные обозначения логических схем одинаковы, независимо от того, из каких элементов они построены.
|
И Y = X1 × Х2 а) |
ИЛИ Y = X1 + Х2 б) |
НЕ
Y =
в) |
|
ИЛИ-НЕ
Y =
г) |
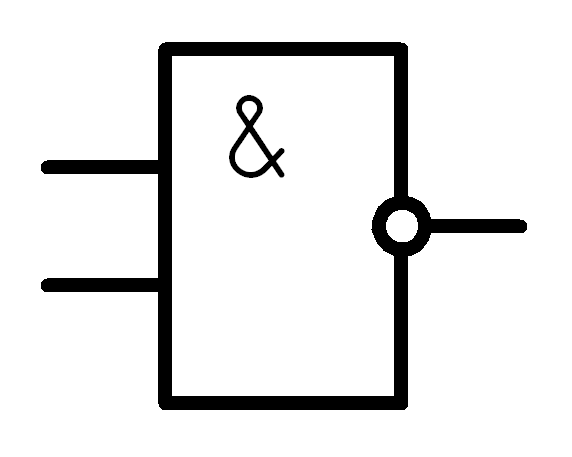
И-НЕ
Y = д) |
Рисунок 1.3.1
Эти логические элементы, кроме инвертора НЕ, реализуют функции двух переменных X1 и Х2 , т.е. являются двухвходовыми. Выпускаются также логические элементы с большим числом входов (до восьми) и более сложной схемой, например, двухступенчатые 2ИЛИ-2ИЛИ-И (рис. 1.3.2).
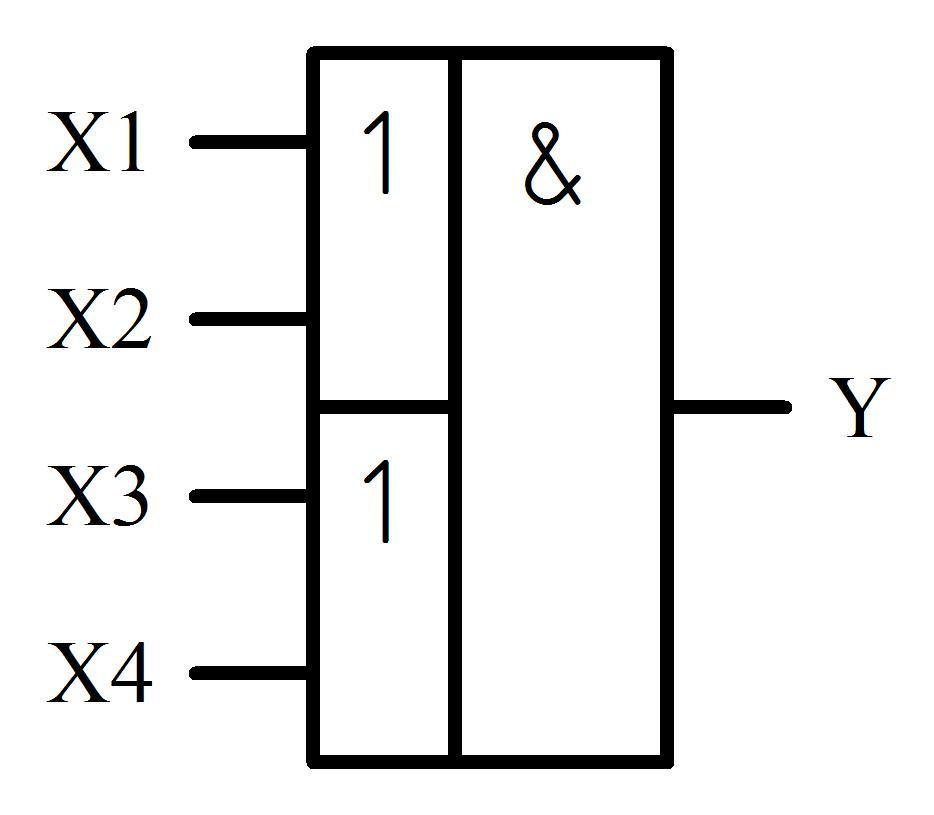
Рисунок 1.3.2
Глава 1.4 комбинационные логические схемы.
Логические вентили, описанные в предыдущей главе, представляют собой элементарные базовые компоненты, из которых строятся логические системы. Сложные логические системы, ЭВМ и микропроцессоры в том числе, представляют собой системы из логических вентилей, которые объединены в типовые логические узлы - триггеры, регистры, счетчики, дешифраторы, системы шин, схемы выполнения арифметических операций и т.д. Все множество логических схем делится на два класса - комбинационные логические схемы и последовательные логические схемы.
КОМБИНАЦИОННЫЕ логические схемы предназначены для выполнения определенных логических операций, и их выходная логическая функция определяется лишь комбинацией входных переменных, поступающих на входы схемы в данный момент времени, и не зависит от их комбинации в предшествующее время. Иными словами, сигнал на выходе таких схем полностью определяется комбинацией входных сигналов.
Многие логические схемы обладает тем свойством, что их выходные значения зависят не только от текущих значений входов, но и от их значений в прошлом. Такие схемы обладает памятью и называется ПОСЛЕДОВАТЕЛЬНЫМИ.
Если алфавит, применяемый на входе и выходе комбинационной схемы чисто двоичный, то каждому двоичному коду на входе комбинационная схема ставит в соответствие определенный код на выходе.
Любую комбинационную схему, имеющую m выходов, можно заменить набором из m комбинационных схем, каждая из которых имеет только один выход и такое же количество входов, как и исходная схема. Очевидно, для постройки любой комбинационной схемы достаточно научиться составлять (синтезировать) произвольную комбинационную схему с одним выходом. К таким схемам, в частности, относятся схемы И и ИЛИ.
Из двухвходовых схем И и ИЛИ можно легко создать схемы с любым количеством входов (см. рис. 1.4.1-1.4.4)
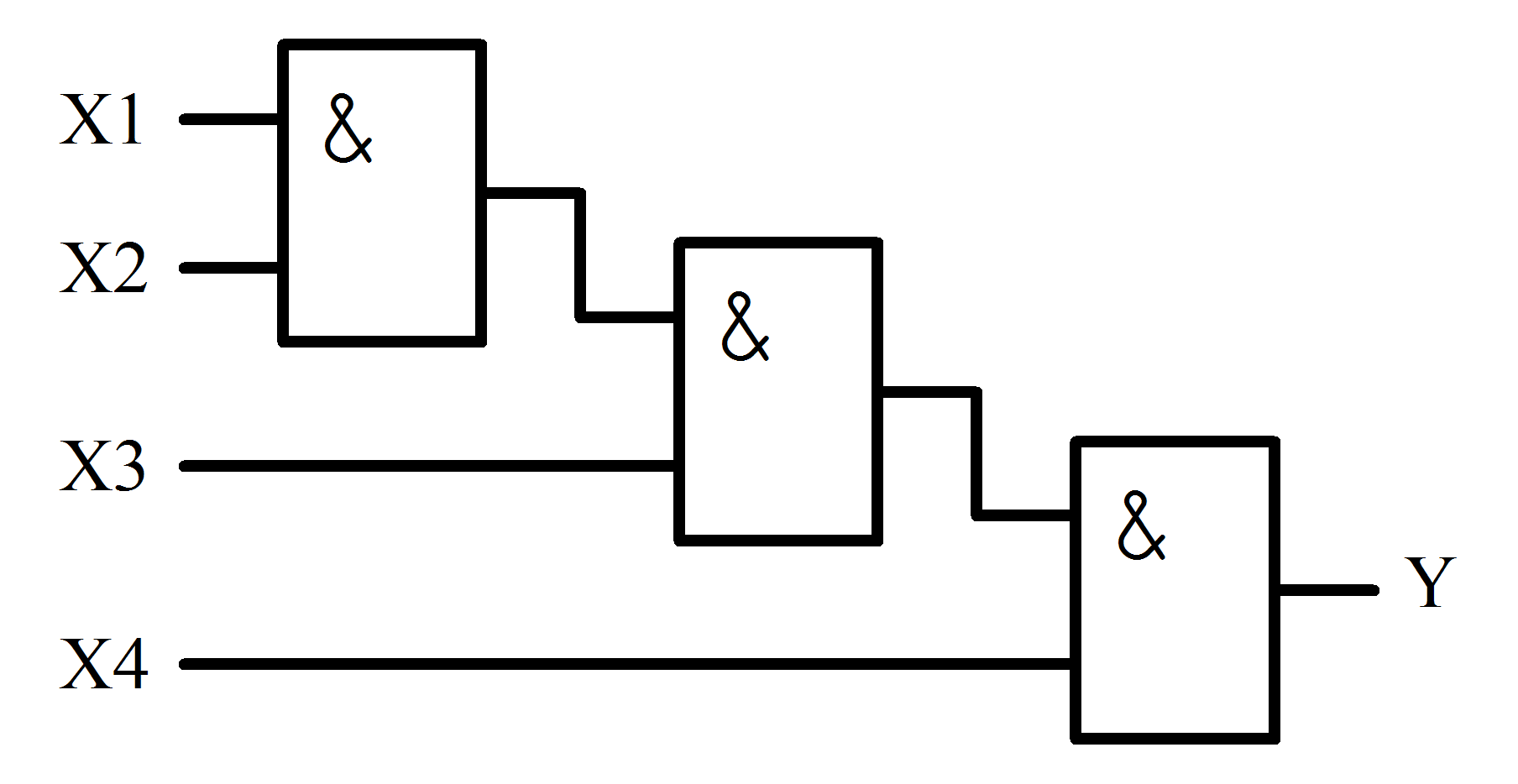
Y = X1 × Х2 × ХЗ × Х4
Рисунок 1.4.1
Обозначение новой схемы:
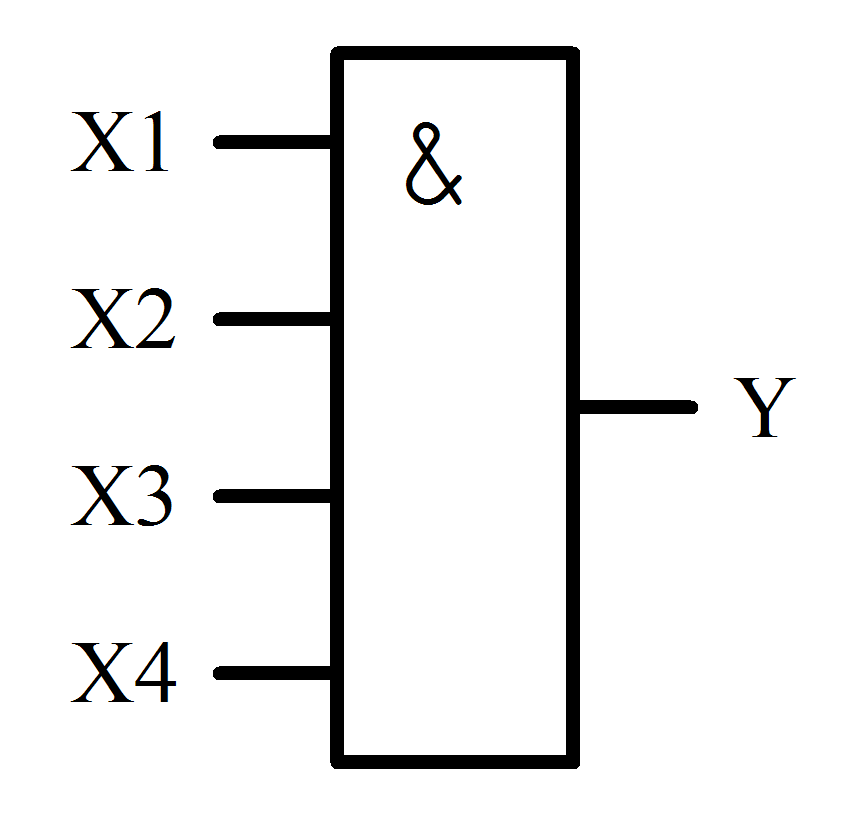
Рисунок 1.4.2
Y = X1 + Х2 + Х3 + X4
Рисунок 1.4.3
Обозначение новой схемы:
Рисунок 1.4.4
Любую другую комбинационную схему также можно синтезировать путем соединения между собой схем И, ИЛИ, НЕ.
Свойства комбинационной схемы полностью определяет таблица истинности соответствующей логической функции. Поэтому чаще всего синтез желаемой логической схемы начинают с составления такой таблицы, которая в простой форме дает алгоритм работы будущей схемы. Такая таблица показывает, какой сигнал должен быть на выходе при каждом возможном наборе сигналов на входах. Однако непосредственно по таблице синтезировать логическую схему весьма затруднительно. Для синтеза произвольной комбинационной схемы, по заданной таблице получают выражение булевой алгебры, описывающее работу схемы. Затем производят упрощение этого выражения (минимизацию) и по полученному минимизированному выражению составляют искомую схему.
Один из способов такого синтеза основывается на использовании, так называемых, ПРОСТЫХ КОНЪЮНКЦИЯ. При числе переменных n (т.е. при синтезе n-входовой схемы) число простых конъюнкций равно 2n. В таб. 1.4.1 и 1.4.2 показано, как образуются простые конъюнкции для n=2 и n=3. При большем n принцип остается прежним.
|
Табл.1.4.1
n = 2
|
Табл.1.4.2
n = 3 |
Из таблиц видно, что данному набору переменных соответствует простая конъюнкция, т.е. произведение всех без исключения переменных, в котором переменные, равные 0, берутся со знаком инверсии, а равные 1 - без него.
Так, например,
простая конъюнкция для набора Е = 0, D
= 1, С = 0, В = 0, А = 1 есть
Выражение булевой алгебры для описания синтезируемой схемы получают на основании теоремы: любая булева функция может быть представлена в виде логической суммы простых конъюнкций, соответствующих тем наборам переменных, при которых эта функция принимает значение 1. В качестве примера найдем булево выражение для схемы ИЛИ - НЕ.
По определению, результат на выходе схемы ИЛИ-НЕ должен являться инверсией сигнала на входе схемы ИЛИ для данной комбинации сигналов на входах. В соответствии с этим составляем таблицу истинности для элемента ИЛИ - НЕ (табл.1.4.3; см.табл.1.2.4 )
Табл.1.4.3
|
X1 |
X2 |
Y |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
0 |
Для этой схемы единица на выходе появляется при одном наборе X1 = 0 , Х2 = 0 , поэтому
Y
=
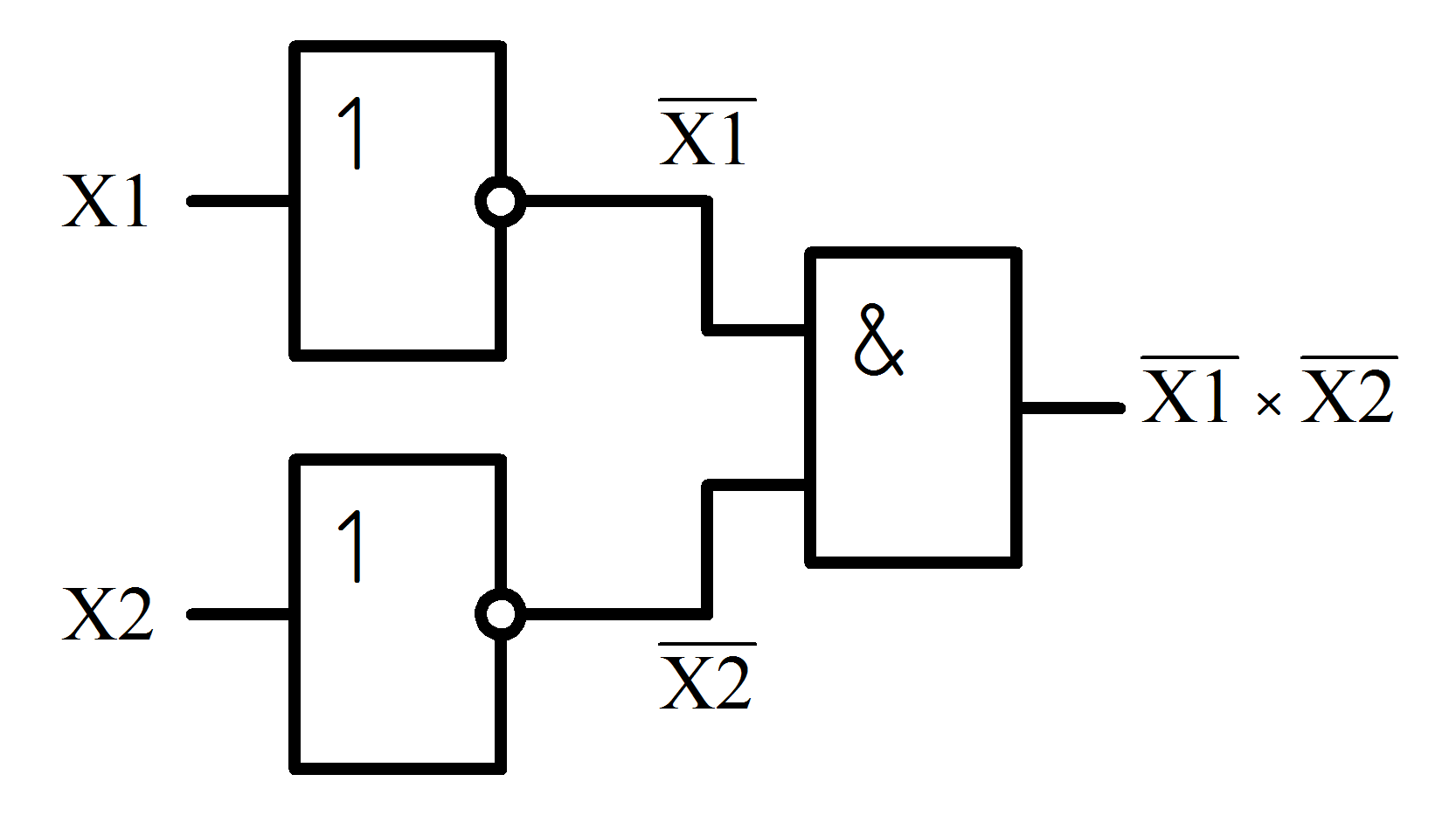
По полученному булеву выражению видно, что получить такую схему можно из схемы И, если поставить перед каждым из ее входов по инвертору (рис.1.4.5).
|
а) |
б) |
Рисунок 1.4.5
Многие из выражений, составленные по сформулированной выше теореме, получаются излишне громоздкими и их минимизируют, т.е. упрощают. Для минимизации применяют аксиомы и законы булевой алгебра. Дело это не сложное, но не имеющее четкого алгоритма, т.е. зависит от опыта и таланта разработчика.