матан11

Любой интервал содержащий точку х0 наывается окрестностью этой точки.

Выколотой окрестностью точки х0 назыв ее окрестность из которой выбрашена сама т х0

] заданы 2 множества х y и правило ставящее в соответствие к каждому эл х € Х ед эл. Y €X f: x→y или x→Y

] f:x→y где x€ R тогда говорят что задана чи)словая функция f.y.=f(x ) пример y = sin x.

A называется пределом ф-и f в т x0 если . €0(A,)

2. предел функции в точке теоремы о единстве предела и об ограниченности функции имеющей конечный предел

Т1 Если предел функци в т х0

Т2 если фу-ия имеет конечный предел в т 0, то в кот ф-ия ограничена

Выполняется неравенство U(f(x)-A)<

3, Предел функции в точке теорема о сохр знака ф-ии и о переходе к пределу в неравенствах

Если ф-ия имеет в т х0 предел отличный от нуля то существует окрестность этой точки (мб U(x0)) в которой ф-ия не равна нулю и имеет тот же знак что и предел. Док-во -

1)если АЮ0 то возьмем 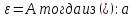<f(x)

2)если А<0 то возьм

Т( о переходе к пределу в неравенствах ] fи g определены на ( аb) и x0( теорема доказана)

4. предел в функции . теорема об ограниченности1/f(x) и о сжатой переменной

если конечный 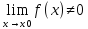то тогда ф-ия 1/f(x) ограничена в 0(х0). ] f и g ,f определены на (a,b)

x0

5. бесконечно малаяф-ия в точке и их св-ва . ф-я Ф-ия - б.м. в т х0<=> такое что для всех х для кот верно 0<

Т1когда она в виде f(x)=A+где бескокн м. в т. Х0. Док-во по опре ф-ии. такое что для всех х удовл неравенству 0<< (x)-A б.м. в т. Х0.

Т2 сумма конечного числа ф-ии б.м в т х0 есть ф-ия б.м. в т. Х0. Д-во - б.м. в т. Х0 т.е.>0 <тогда для всех х уд-х неравенству 0< / <=

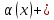
Т3 ф-я б.м. в т х0 ограничен в некоторой 0(х0)

Т4 Произведение ф-ии ограниченной в окрестности т х0 на ф-ию б.м в т. Х0 есть ф-я б. м. в т х0

Т5 Произведение конечного числа ф-ии б. м в т х0 есть ф-я бесконечно малая в т х0

6. Сравнение б.м.. яэквивалентные б. м. наз сравнение б.м. при этом:

1) =0 a(x) б. М. Более высокого порядка

Тгда говорят что заданоотображение множества Х в мн y

1

Окрестность точки – любой интервал, содерж эту точку.

δ-окрест т +бескон- множество точек вида U(+бескон; δ)={x|x>δ}

δ-окрест т -бескон- множ точек вида U(-бескон; δ)={x|x<-δ}

выколотая

15

Если сущ предел отнош приращ ф и вызвавшему его приращ аргумента при стремл аргум к 0, то этот пред – производная ф в т

Геометрический смысл производной. Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке. f’(x)=tgx

Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан:  координата  x  движущейся точки – известная функция  x ( t ) времени  t. В течение интервала времени от  t₀  до  t₀ +   точка перемещается на расстояние:  x ( t₀ +  ) - x ( t₀ ) = , а её средняя скорость равна:  v_a =  /  . При    0  значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью  v ( t₀ )  материальной точки в момент времени  t₀ . Но по определению производной мы имеем:

отсюда,  v ( t₀ ) = x’ ( t₀ ) , т.e. скорость – это производная координаты по времени. В этом и состоит  механический смысл производной.Аналогично, ускорение – это производная скорости по времени:  a = v’ ( t ).

16.

Определение Функция y=f(x) называется дифференцируемой в точке x0, если ее приращение Δy в точке x0 может быть представлено в виде: Δy=A·Δx+α(Δx)·Δx, где A -- некоторое число, независящее от Δx, а α(Δx)-- бесконечно малая функция от переменной Δx, т.е. limΔx→0α(Δx)=0.

 

Теорема Для того, чтобы функция y=f(x) была дифференцируема в точке x0, необходимо и достаточно, чтобы она в этой точке имела конечную производную. Доказательство  Необходимость. Предположим: функция дифференцируема в точке x0, т.е. Δy=A·Δx+α(Δx)·Δx. Разделив обе части данного равенства на Δx, получим: ΔxΔy=A+α(Δx). Из определения производной функции в точке: y/(x0)=limΔx→0ΔxΔy=limΔx→0(A+α(Δx))=A.

Т.е. получили, что существует конечная производная функции в точке x0 и y/(x0)=A. Достаточность. Пусть существует конечная производная y/(x0)∈R . Покажем дифференцируемость функции. y/(x0)=limΔx→0ΔxΔy.

Если функция f(x) имеет конечный предел b при Δx→0 , то ее можно представить: f(x)=b+α(x) (α(x)→0) . Исходя из этого: ΔxΔy=y/(x0)+α(Δx), где limΔx→0α(Δx)=0, Δy=y/(x0)·Δx+α(Δx)·Δx→ A=y/(x0) . Теорема доказана.

17

Непрерывность дифференцируемой функции

Теорема 1. Пусть функция y = f(x) дифференцируема на интервале (a, b). Тогда функция fнепрерывна на (a, b).

Доказательство

Возьмем произвольное фиксированное число x  (a,b).

По условию теоремы

Следовательно, в малой окрестности числа x₀ можно определить функцию α = α(Δx), стремящуюся к нулю при  такую, что

Но тогда  и, следовательно, функция f непрерывна при x = x₀. Так как число x₀ – произвольное, то функция fнепрерывна на всем интервале (a, b).

Теорема доказана.

19

Правила дифференцирования обратной функции.

Теорема

Пусть функции y=f(x) удовлетворяет всем условиям теоремы о  обратной функции  и имеет в точке  производную , тогда обратная функция  так же имеет производную в соответствующей точке  и справедлива формула  (6).  Дадим аргументу y обр. ф-ции в точке  приращение  тогда в силу строгой монотонности обр. ф-ции ее приращение  в точке  будет отлично от 0 и поэтому можно записать . Перейдем в этом равенстве к пределу при  (при этом  в силу непрерывности функции y=f(x) в т. ).  Следовательно предел слева также  и по определению производной есть производная . Окончательно: . Геометрическая иллюстрация.  имеем:

 

 

Производные основных элементарных функций. 1. , где   (7) эта формула будет доказана позже. 2.

; (8)

(9)

формулы (8) и (9) доказываются с помощью определения производной, 1 замечательного предела и непрерывности функции cos(x) и sin(x) соответственно. 3.

y=tg(x);  где

y=ctg(x)

Формулами (10) и (11) доказываются с использованием правила дифференцирования частного и формул (8) и (9). 4.  где   (12)  ; перейдем к lim при  пусть  при   (2-ой замечательный предел).

 

Поэтому с учетом непрерывности логарифмической функции  или , если a=e . . 5.

y=arcsin(x)  (13)

y=arccos(x)  (14)

 т.к. на    то корень арифметический по теореме о производной обратной функции  (13). Формула (14) доказывается аналогично или с помощью  6.

y=arctg(x)  (15)

y=arcctg(x)  (16)

 по теореме о производной обратной функции . Формула (16) доказывается аналогично. 7.  где   по теореме о производной обратной функции имеем  таким образом ;  (17).

В частности, если a=e,  (18). 8.

y=sh(x)  (19)

y=ch(x)  (20)

  Доказательство формулы (20). Имеем 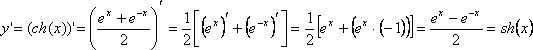. Формула (19) доказывается аналогично. 9.

(21)

(22)

При доказательстве используется производная частного, а потом формулы (19) и (20).

20

Линейную функцию  называют дифференциалом функции f в точке  и обозначают df. Для функции x производная в каждой точке  равна 1, то есть  Поэтому пишут: 

21

Пусть функция y=f(x) дифференцируема на множестве Х. Если сущ произв от 1 произв, то её называют производной второго порядка функции у= f(x) или , короче, второй производной и обозначают f''(x) или у''.

Вообще производной n-го порядка называют производную от производной (n-1)- го порядка  и обозначают 

Пусть f дважды диф на Х. Диф от диф ф f – диф 2-ого порядка или 2 диф f

d² f(x) = d (df(x) ) = d (f'(x) dx) = f''(x) dx · dx + f'(x) · d(dx)

22

Теорема Ферма. Пусть ф-ция f(x) определена на интервале <a,b> и в некоторой т-ке х0 этого интервала имеет наибольшее или наименьшее знач. Тогда если в т-ке х0 сущ пр-ная, то она = 0, f’(x0)=0.

Д-во: пусть f(c)-наим знач; пусть x принадл <a;b>

(f(x)-f(c))/(x-c)=[+/-=-,x<c / +/+=+, x>c

f’(c минусом)(c)=lim(x->c-0)(f(x)-f(с))/(x-c)< или =0,

f’(c плюсом)(с)= lim(x->c-0)(f(x)-f(с))/(x-c)> или =0,

но сущ f’©=> 0< или =f’(c)< или =0 и f’(c)=0

Теорема Ролля. Пусть на отрезке [a,b] определена ф-ция f(x) причем: f(x) непрерывна на [a,b]; f(x) диф. на (a,b); f(a)=f(b). Тогда сущ т-ка с принадл(a,b), в которой f‘(c)=0.

Д-во: по 2 теор Вейерштрасса f достигает [a;b] своего наим (m) и наиб (M) знач.

1). Пусть m=M, т.е. m<или=f(x)<или=M=m след f(x)=m

f(x)=const=>f’(x)=0 и т.с принадл(a;b)

2). Пусть m<M. Тогда хотя бы 1 из этих знач достиг в т.с [т.к. f(a)=f(b)]=>по т.Ферма f’(c)=0.

23

Теорема Логранджа. Пусть на отрезке [a,b] определена и непрер f(x), имеет кон произв по кр мере на (a;b). Тогда сущ т-ка c принадл (a,b) такая, что справедлива ф-ла (f(b)-f(a))/b-a= f’(c).

Зам. Это формула конечных приращений. f(b)-f(a)=f’(c)(b-a)

На [x0;x](или [x;x0]) f(x)-f(x0)=f’(c)(x-x0) x0<c<x или наоборот

Теорема Коши. Пусть ф-ции f(x) и g(x) непр. на [a,b] и диф. на (a,b). Пусть кроме того, g`(x)не =0. Тогда сущ т-ка с принадл(a,b) такая, что справедл. ф-ла (f(b)-f(a))/(g(b)-g(a))=f‘(c)/g‘(c). (2)

1). Докажем,что g(a)не =g(b). Предпол, что g(b)=g(a). Тогда для g возможн все 3 усл т.Ролля. значит, сущ с принадл (a;b):g’(c)=0. g(b)не =g(a).

2). Докажем, что (2)верна.

Введем вспомог F(x)=f(x)-f(a)-(f(b)-f(a))/(g(b)-g(a))(g(x)-g(a)) верны 3 усл т.Ролля. F(x): 1 непрер на [a;b] 2 сущ F’(x) на (a;b): F’(x)=f’(x)-(f(b)-f(a))/(g(b)-g(a))g’(x) (*) 3 F(a)=f(a)-f(a)-(f(b)-f(a))/(g(b)-g(a))(g(a)-g(a))=0 4 F(b)=f(b)-f(a)-(f(b)-f(a))/(g(b)-g(a))(g(b)-g(a))=0 Т.е. F(a)=F(b)=0 => ф-я F(x) удовл усл т.Ролля => сущ т. С принадл (a;b):F’(c)=0 Из (*) => f’(c)-(f(b)-f(a))/(g(b)-g(a))g’(c)=0  (f(b)-f(a))/(g(b)-g(a))=f‘(c)/g‘(c).

24

Пусть f

Опред на (а;b), x0 принадл (a;b) и f непрер в т. Х0. Если сущ U(х0) такая, что 1). f(х)меньше или =f(х) для всякого икс из этой окрест, то икс – т.локал.макс f. 2). f(x) больше или =f(х0) для всякого х, то х0 – т.локал мин. 3). Локал макс и мин – локал экстремумы. 4). Если нер-ва в 1) и 2) строг, то экстрем – строгие.

Пусть f опр в U(х0) и х0 – т.экстр f. Если сущ f’(х0), то f’(х0)=0

Д-во: по т.Ферма

Зам 1.из этого след, что f может иметь экстр только в таких т, где она непрер, а ее f’ либо =0, либо не сущ

Зам 2.Условие f’(x)=0 не явл достат для экстр (y=x^3)

25

Пусть f опред в U(х0) и сущ конечн пред в м.б. выколот U(х). Если при переходе через т х0(слева направо) f’(x):

1). Меняет знак с + на -, то х0 – т.строг локал макс

2). Меняет знак с – на +, то х0 – т.строг локал мин

3). Не меняет знак, то экстр в . х0 нет.

Д-во: 1). Пусть х принадл U(х0), f(x)-f(x0)=f’(c)(x-x0)

а)пусть x<x0 => x<c<x0

x-x0<0; f’(c)>0 => f(x)-f(x0)<0 и f(x)<f(x0)

б)x>x0 => x0<c<x0

x-x0>0; f’(c)<0 => f(x)-f(x0)<0 и f(x)<f(x0)

Итак, для всех х принадл выколот U(x0) f(x)<f(x0)

2) аналог

3) пусть f’(x)<0 => f(x)движ вниз в U(x0) и в . х0 экстр нет

Зам. Экстремумы – локал, м.б. знач f в т.локал.мин>знач f в т.локам макс

2) экстр надо искать среди т, где f’(x)=0 (стац) и среди т, где f’(x) – не сущ (особ) стац+особ=крит т 1ого рода

26

Пр.Лопиталя

1 f и g опред и непрер на (a;b]

2 lim(x->a+0)f(x)= lim(x->a+0)g(x)=0

3 сущ кон f’(x) и g’(x) на (a;b)

4 g’(x) не =0

5 сущ кон или бескон lim(x->a+0)(f’(x)/g’(x))=A

Тогда сущ lim(x->a+0)(f(x)/g(x))=A

Зам 1 преб мб односторонним

2 предел мб в т +/- бесконечн

3 неопределенность мб {бескон/бескон}

4 другие виды неопределенности нужно приводить к виду {0/0} или {бескон/бескон}

27

Пусть f опред и непрер на (a;b). Тогда говорят,что:

1 f выпукла вверх на (a;b) если все точки лежат ниже всякой ее касательной

2 f выпукла вниз,если все т лежат выше ее касат

Т5

Пусть f дважды дифф на (a;b). Тогда если

1 f’’(x)<0 на (a;b) то f – выпукла вверх на (a;b)

2 f’’(x)>0 на (a;b) то f – выпукла вниз на (a;b)

Д-во: y=f(x) y(кас)=f(x0)+f’(x0)(x-x0)

y-y0=f(x)-f(x0)-f’(x0)(x-x0)={сущ т с между х и х0:}=f’©(x-x0)-f’(x0)(x-x0)-(x-x0)(f’(c)-f’(x))={по Т.Логранжа сущ с1 между с и х0}=f’’(c1)(c-x0) (*)

1 x<x0 f’’(c1)<0 c-x<0 x-x0<0 => y-y(кас)<0 т.е. y<y(кас)

2 x>x0 f’’(c1)<0 c-x>0 x-x00 => y-y(кас)<0 т.е. y<y(кас)

Итак, в любом случае y<y(кас) => f выпукла вверх

Зам. Усл Т5 дост,но не явл необх

28

Пусть f непрер в т х0 и при переходе через т х0 меняет направл выпукл. Тогда т х0 наз точкой перегиба графика ф-ии

Необх

Пусть f дважды непрер дифф на (a;b). Если х0 принадл (a;b) и х0 – точка перегиба, то f’’(x0)=0

Д-во: от противн. Пусть например f’’(x0)>0/ тогда по непрер f’’(x)>0 в некот U(x0) => f(x) выпукла вниз и слева от т.х0,т.е.т.х0-не т.перегиба

Зам. Усл f’’(x0)=0 не явл достат. Пример: y=x^4 y’=4x^3 y’’=12x^2

y’’=0, но это не т перегиба

дост

пусть f опред и непрер в U(x0) и дважды дифф в мб выколот U(x0). Если f’’(x) меняет знак при переходе через х0,то х0-т перегиба

Д-во:

Зам. Таким образом, перегибы графика f мб в т, где f’’(x)=0 или не сущ

Это крит т 2ого рода

29

30

1 ООФ 2 Периодичность, четность/нечетность 3 точки разрыва 4 вертикальные ассмптоты 5 наклонн или горизонт асимптоты 6 монотонность, экстрем 7 направл выпукл и т перегиба 8 доп точки 9 построение графика

33

f(x)=e^x f^(n)(x)=e^x

y=sinx y^(n)=sin(x+*пи*n/2)

y=cosx y^(n)=cos(x+*пи*n/2)

34

y=ln(1+x) y^(n)=(-1)^(n-1)(n-1)!/(1+x)^n

y=(1+x)^*альфа* y^(n)= *альфа*(*альфа*-1)…(*альфа*-n+1)(1+x)^(*альфа*-n)