
Понятие окрестности точки
Абсолютная величина (или модуль) действительного числа х - это само число х, если х неотрицательно, и противоположное число -х, если х отрицательно:
![]()
Некоторые свойства абсолютных величин:
|х| ≥ 0 (по определению);
|х + y| |х| + |y|;
|х - y| ≥ |х| - |y|;
|хy| = |х||y|;
|х/y| = |х|/|y|.
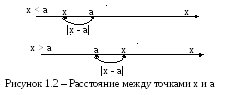 Абсолютная
величина разности двух чисел |х - а|
означает расстояние между точками х и
а числовой прямой как для случая х <
а, так и для х > а (см. рис. 1.2). Поэтому,
например, решениями неравенства |х - а|
<
(где
> 0) будут точки х интервала ]а - ,
а + [.
Абсолютная
величина разности двух чисел |х - а|
означает расстояние между точками х и
а числовой прямой как для случая х <
а, так и для х > а (см. рис. 1.2). Поэтому,
например, решениями неравенства |х - а|
<
(где
> 0) будут точки х интервала ]а - ,
а + [.
Окрестность точки. Всякий интервал, содержащий точку а, называется окрестностью точки а.
И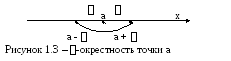 нтервал
]а -,
а + [,
т.е. множество точек х таких, что |х - а|
<
(где
> 0) называется -окрестностью
точки а (см. рис. 1.3).
нтервал
]а -,
а + [,
т.е. множество точек х таких, что |х - а|
<
(где
> 0) называется -окрестностью
точки а (см. рис. 1.3).
Функциональная зависимость
Постоянной величиной (константой) называется величина, сохраняющая одно и то же значение.
Переменной называется величина, которая может принимать различные числовые значения.
Функция – это соответствие (закон), согласно которому каждому элементу х множества X (х X) ставится в соответствие вполне определенный элемент у множества Y (у Y) (этот элемент y обязательно должен быть только один для любого х)..
При этом говорят, что на множестве X задана функция y = f(x).
Переменная х называется независимой переменной (или аргументом), у - зависимой переменной, а буква f обозначает закон соответствия.
Множество X называется областью определения (или существования) функции, а множество Y - областью значений функции.
Если множество X специально не оговорено, то под областью определения функции подразумевается область допустимых значений независимой переменной х, т.е. множество таких значений х, при которых функция у = f(х) вообще имеет смысл.
Например,
область определения функции
![]() есть промежуток [5; +[,
так как под знаком корня должно стоять
неотрицательное выражение (х – 5 ≥ 0).
есть промежуток [5; +[,
так как под знаком корня должно стоять
неотрицательное выражение (х – 5 ≥ 0).
Способы задания функций. Существует несколько способов задания функций:
а) Аналитический
способ, если функция задана формулой
вида
y = f(x). Этот способ наиболее часто
встречается на практике. Например,
функция
![]() задана аналитически.
задана аналитически.
С
помощью формулы функция может быть
задана явно
или неявно.
Задание будет явным, если правая часть
формулы не содержит зависимую переменную.
Например, в формуле
![]() правая часть не содержит y, поэтому
функция задана явно. Пример неявного
задания функции – выражение x3
+ y2
= 2. С помощью этого выражения неявно
заданы две функции –
правая часть не содержит y, поэтому
функция задана явно. Пример неявного
задания функции – выражение x3
+ y2
= 2. С помощью этого выражения неявно
заданы две функции –
![]() для y
> 0 и
для y
> 0 и
![]() для
y
< 0.
для
y
< 0.
б) Табличный способ состоит в том, что функция задается таблицей, содержащей значения аргумента х и соответствующие значения функции f(x). Например, прайс-лист, в котором каждому номеру товара соответствует его цена.
в) Графический способ состоит в изображении графика функции - множества точек (х, y), абсциссы которых есть значения аргумента х, а ординаты - соответствующие им значения y (см. рисунок 1.3).
Основные свойства функций
1. Четность и нечетность. Функция y = f(x) называется четной для любых значений х из области определения, если f(-x) = f(x), и нечетной, если f(-x) = -f(x). В противном случае функция называется функцией общего вида.
Например, функция у = х2 является четной, так как (-х)2 = х2; а функция у = х3 – нечетной, так как (-х)3 = -х3. Функция у = f(x) = х2 +х3 является функцией общего вида, так как f(-x) = (-х)2 +(-х)3 = х2 - х3. При этом f(-x) f(x) и f(-x) - f(x).
График четной функции симметричен относительно оси ординат (например, функции у = х2), а график нечетной функции симметричен относительно начала координат (например, график функции у = х3).
2. Монотонность. Функция y = f(x) называется возрастающей (убывающей) на некотором промежутке, еcли большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.
Пусть х1, х2 X и х2 > х1. Тогда функция возрастает на промежутке X, если f(x2) > f (х1) и убывает, если f(x2) < f (х1).
В обоих случаях функции называются строго монотонными. Если два последних неравенства – нестрогие (т.е. f(x2) ≥ f (х1) и f(x2) f (х1)), то функции называют соответственно неубывающими и невозрастающими.
Например, функция у = х2 убывает для неположительных значений аргумента (т.е. на промежутке ]-; 0]) и возрастает для неотрицательных.
3. Ограниченность. Функцияy= f(x) называетсяограниченнойна некотором промежуткеX, если существует такое положительное число М, что модуль значения функции не превышает этого числа для любого аргумента из этого промежутка. (М > 0: |f(x)|Mдля любого хX)
В противном случае функция называется неограниченной.
Например, функция у = cosх ограничена на всей числовой оси, так как |cosх|1. Функция у = х не ограничена на ]-; +[.
Если в определении рассматривать не модуль значения функции, а само значение, которое должно быть не меньше или не больше числа М, то можно говорить об ограниченности снизу или сверху.
4. Периодичность. Функция y = f(x) называется периодической с периодом Т 0, если для любых х из области определения f(х + Т) = f(x).
Например3, функция у = sin х имеет период Т = 2, так как sin (х +2) = sin х.
Обратная функция. Если для функции y = f(x) различным аргументам х1 х2 соответствуют различные значения функции y1 y2, то можно определить функцию x = (y), которая каждому число y = f(x) ставит в соответствие число х. Такую функцию называют обратной для f и обозначают f-1.(не следует путать это обозначение с возведением в степень (-1)).
Из этого определения следует, что для любой строго монотонной функции существует обратная функция.
Например, для функции у=ах обратной будет функция x=lоgaу (или в обычных обозначениях зависимой и независимой переменных у= lоgах).
Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов (относительно прямой y = x) (см. рис. 1.3).

Сложная функция. Пусть функция y = f (u) есть функция от переменной u, определенной на множестве U c областью значений Y, а переменная u, в свою очередь, является функцией u = (х) от переменной х, определенной на множестве X с областью значений U. Тогда заданная на множестве X функция y = f [ (х)] называется сложной функцией (или композицией функций, суперпозицией функций, функцией от функции).
Например, у = lg sin х — сложная функция, так как ее можно представить в виде у= lg u, где u = sin х.
