Вариационный ряд. Статистические распределения. Эмпирическая функция распределения

Полученная в результате статистического наблюдения выборкаизnзначений (вариант) изучаемого количественногопризнака Xобразуетвариационный ряд.Ранжированныйвариационный ряд получают, расположив вариантыx_j , гдеj=1, 2, ... ,n,в порядке возрастания (неубывания) значений, то есть_.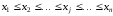

Изучаемый признак Xможет бытьдискретным, то есть его значения отличаются на конечную, заранее известную величину (год рождения, тарифный разряд, число людей), илинепрерывным, то есть его значения отличаются на сколь угодно малую величину (время, вес, объем, стоимость).

Частотойm_i в случаедискретногопризнакаXназывают число одинаковых вариантx_i, содержащихся в выборке. В ранжированном вариационном ряду одинаковые варианты очевидно расположены подряд:

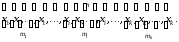
Вариационный ряд для дискретногопризнакаXпринято наглядно и компактно представлять в виде таблицы, в первой строке которой указаныkразличных значенийx_iизучаемого признака, а во второй строке - соответствующие этим значениям частотыm_i , гдеi=1, 2, ... ,k. Такую таблицу называютстатистическим (выборочным) распределением.

Переход от исходного вариационного ряда дискретного признака Xк соответствующему статистическому распределению поясним на простом примере.

Вариационный ряд, полученный в результате статистического наблюдения (единицы измерения опускаем), - 7, 17, 14, 17, 10, 7, 7, 14, 7, 14.

Ранжированный вариационный ряд - .

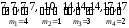Тогда соответствующее статистическое распределение (i = 1, 2, ...,k,k=4) примет вид

xi	7	10	14	17
mi	4	1	3	2	.

Статистическое распределение для непрерывногопризнакаXпринято представлятьинтервальным рядом- таблицей, в первой строке которой указаныkинтервалов значений изучаемого признакаX вида (x_i-1 - x_i ), а во второй строке - соответствующие этим интервалам частотыm_i , гдеi=1, 2, ...,k. Обозначение (x_i-1 - x_i ) указывает не разности, а все значения признакаX отx_i-1доx_i , кроме правой границы интервалаx_i .

Для непрерывногопризнакаXчастотаm_i - число различныхx_j , попавших в соответствующий интервал (x_i-1 - x_i ).

Переход от исходного вариационного ряда непрерывного признака Xк соответствующему статистическому распределению поясним на простом примере.

Вариационный ряд, полученный в результате статистического наблюдения (единицы измерения опускаем), - 3,14; 1,41; 2,87; 3,62; 2,71; 3,95.

Ранжированный вариационный ряд - 1,41; 2,71; 2,87; 3,14; 3,62; 3,95.

Получим соответствующее статистическое распределение (i=1, 2, …,k,k = 3)

xi	1-2	2-3	3-4
mi	1	2	3	.

Если число различных значений дискретного признака очень велико, то для удобства дальнейших вычислений и наглядности статистическое распределение такого дискретного признака также может быть представлено в виде интервального ряда.

Вместо частот m_iво второй строке могут быть указаныотносительные частоты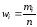(частости). Очевидно, что сумма частот равна объему выборки (выборочной совокупности)n, а сумма относительных частот (частостей) равна единице:

.

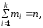
Далее показаны четыре возможные формы представления статистических распределений с соответствующими краткими названиями.

Дискретный ряд частот:

Интервальный ряд частот:

xi

x1

x2

…

xk

xi-1-xi

x0-x1

x1-x2

…

xk-1-xk

mi

m1

m2

…

mk

.

mi

m1

m2

…

mk

.

Дискретный ряд частостей:

Интервальный ряд частостей:

xi

x1

x2

…

Xk

xi-1-xi

x0-x1

x1-x2

…

xk-1-xk

wi

w1

w2

…

wk

.

wi

w1

w2

…

wk

.

Если в статистическом распределении вместо частот (относительных частот) указать накопленные частоты (относительные накопленные частоты), то такой ряд распределения называют кумулятивным.

Накопленной частотойназывается число значений признакаХ, меньших заданного значенияx:H(x) =m(Х<x), то есть число вариантx_jв выборке, отвечающих условиюx_j<x.

Переход от дискретного ряда частот к кумулятивному ряду (дискретному ряду накопленных частот) задается соотношениями

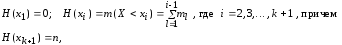
или в табличной форме:

xi	x1	x2	x3	…	xi	…	xk	xk+1
H(xi)	0	m1	m1+m2	…	H(xi-1) + mi-1	…	H(xk-1) + mk-1	H(xk) + mk= n	.

Переход от интервального ряда частот к кумулятивному ряду (интервальному ряду накопленных частот) задается соотношениями

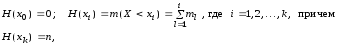
или в табличной форме:

xi-1-xi	-Ґ-x0	x0-x1	x1-x2	…	xi-1-xi	…	xk-1-xk
H(xi)	0	m1	m1+m2	…	H(xi-1) + mi	…	H(xk-1) + mk= n	.

Накопленной относительной частотой(накопленной частостью) называется отношение числа значений признакаХ, меньших заданного значенияx, к объему выборкиn: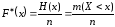, то есть доля вариантx_jв выборке, отвечающих условиюx_j<x.

По аналогии с теоретической функцией распределения генеральной совокупности 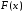=P(Х < ), которая определяетвероятность события Х < , вводят понятиеэмпирической функции распределения 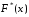, которая определяетотносительную частоту этого же события Х < , то есть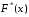=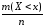. Таким образом,эмпирическая функция распределения 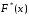задается рядомнакопленных относительных частот.

Из теоремы Бернулли следует, что стремится по вероятности кF(x):

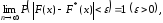
поэтому эмпирическую функцию распределения можно использовать для оценки теоретической функции распределения генеральной совокупности.

Дискретный ряд накопленных относительных частот может быть получен двумя равноправными способами:

1) переход от дискретного ряда частостей к кумулятивному ряду (дискретному ряду накопленных частостей) описывается соотношениями

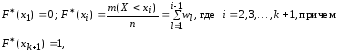
или в табличной форме:

xi	x1	x2	x3	…	xi	…	xk	xk+1
(xi)	0	w1	w1+w2	…	(xi-1) +wi-1	…	(xk-1) +wk-1	(xk) + wk= 1	;

2) переход от дискретного ряда накопленных частот к дискретному ряду накопленных частостей задается соотношением

Интервальный ряд накопленных относительных частот может быть получен двумя равноправными способами:

1) переход от интервального ряда частостей к кумулятивному ряду (интервальному ряду накопленных частостей) задается соотношениями

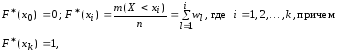
или в табличной форме:

xi-1-xi	-Ґ-x0	x0-x1	x1-x2	…	xi-1-xi	…	xk-1-xk
(xi)	0	w1	w1+w2	…	(xi-1) +wi	…	(xk-1) +wk= 1	;

2) переход от интервального ряда накопленных частот к интервальному ряду накопленных частостей задается соотношением