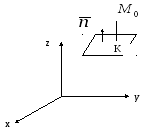
4. Взаимное расположение двух плоскостей в пространстве. Расстояние от точки до плоскости

Дана плоскость и точка(см. рис).

Опустим из точки на плоскость перпендикуляр. Тогда- это расстояние от точки до плоскости. Вектор нормали плоскостиколлинеарен вектору, следовательно,. Пусть точкаимеет координаты. Тогда

.

Так как точка принадлежит плоскости, тои

Отсюда получаем формулу расстояния от точки до плоскости

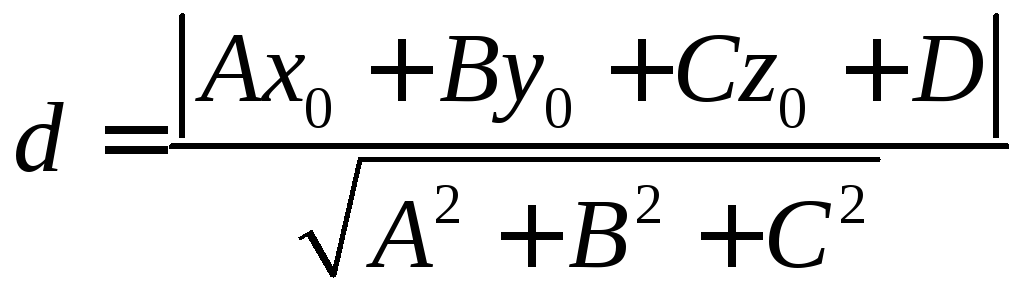. (4.1)

Пусть даны две плоскости:

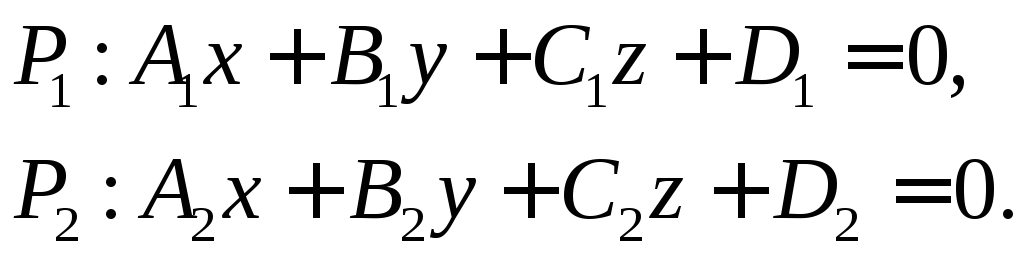
Рассмотрим возможные случаи расположения плоскостей.

1. - это условие параллельности плоскостей, если при этом еще и, то плоскости совпадают.

Если плоскости параллельны, то можно найти расстояние между ними, для этого нужно воспользоваться формулой (4.1): . Координаты точкинаходим из уравнения плоскостиследующим образом: две координаты задаем произвольным образом, например,

, а третью координату находим из уравнения, следовательно, .

2. - это условие перпендикулярности плоскостей .

3.

Пример. Составить уравнение плоскости, проходящей через точку , параллельной плоскости. Найти расстояние от точкидо плоскости.

Решение. Так как искомая плоскость параллельна плоскости , то в качестве ее вектора нормали можно взять вектор нормали плоскости, то есть. Воспользуемся уравнением:

, или

.

Для нахождения расстояния от точки до плоскостивоспользуемся формулой (4.1):

, .

5. Различные уравнения прямой линии в пространстве

Прямая в пространстве может быть получена в результате пересечения двух плоскостей, то есть задана аналитически системой двух уравнений первой степени с тремя переменными.

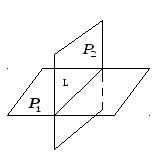
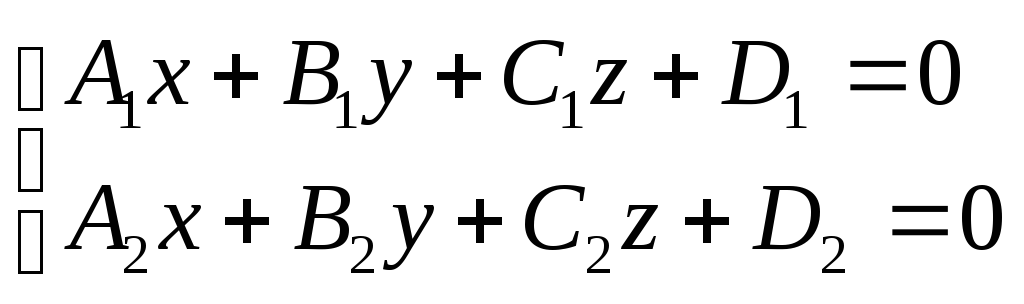(5.1)

Уравнения (5.1) называются общими уравнениями прямой в пространстве.

Положение прямой в пространстве определено, если задана точка , через которую

п

z

роходит прямая, и направляющий вектор прямой.

x

Возьмем произвольную точку на прямой , векторыиколлинеарны, то есть

если направления векторов совпадают, то , в противном случае.

так как , то

(5.2)

это векторное уравнение прямой в пространстве, переходя от векторного уравнения к координатным уравнениям, получим

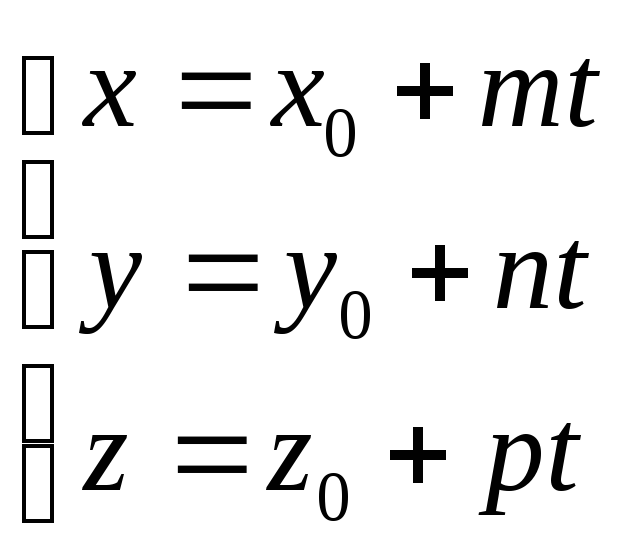(5.3)

это параметрические уравнения прямой в пространстве, - параметр. Если исключить из уравнений (5.3) параметр, получим канонические уравнения прямой в пространстве

. (5.4)

Как перейти от общих уравнений прямой к каноническим?

1. Надо из системы (5.1) найти координаты точки, через которую проходит прямая. Так как система содержит два уравнения, а переменных три, одну из переменных нужно задать произвольным образом, например, , а две другие найти из системы.

2. Так как прямая лежит и в одной, и в другой плоскости, то векторы нормали этих плоскостей перпендикулярны направляющему вектору прямой, следовательно, , тогда

Пример. Даны общие уравнения прямой

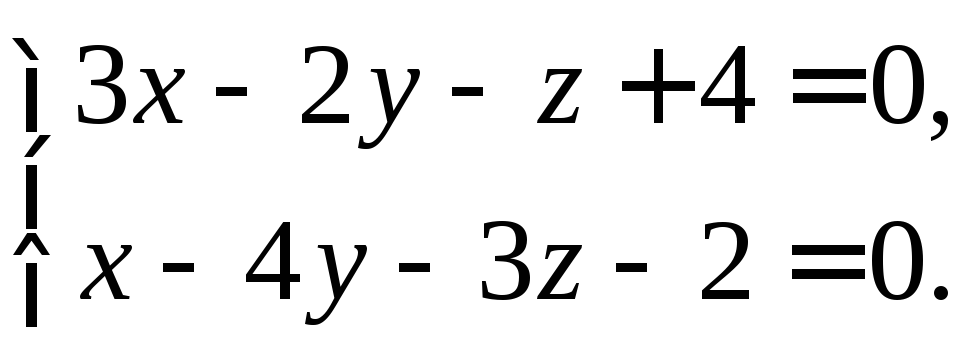
Составить канонические уравнения этой прямой.

Решение. Найдем точку, через которую проходит данная прямая, для этого в системе положим , тогда решая систему, получим.

Теперь найдем координаты направляющего вектора:

,

составляем канонические уравнения прямой:

.

Пусть дана точка и прямая. Надо найти расстояние от точки до прямой.

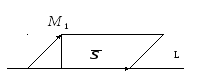
Искомое расстояние – это высота параллелограмма, построенного на векторах и. Найдем площадь параллелограмма, тогда

.