Ekzamen_MEKhANIKA

Шары движутся в горизонтальной плоскости, поэтому их потенциальная энергия в поле тяготения Земли при ударе не изменяется, т.е.

Тогда из уравнения (3.15) получаем:

(3.16)

С другой стороны, по закону сохранения импульса

(3.17)

При центральном ударе векторы скоростей u1, u2, v1 и v2 направлены вдоль одной прямой. Поэтому в уравнении (3.17) можно перейти от векторов к их модулям:

(3.18)

Решая совместно уравнения (3.16) и (3.18), получим:

(3.19)

Анализ уравнений (3.19) позволяет сделать следующие выводы:

1)Если массы шаров одинаковы (m1=m2=mn), то u1=v2 и u2=v1, т.е. при ударе шары обмениваются скоростями;

2)если масса второго шара m2 >> m1, то

Если при этом второй шар был до удара неподвижен (v2 = 0), то u1 ≈ -v1; u2 = 0, т.е. первый шар отскакивает от неподвижного массивного шара и движется в обратную сторону со скоростью u1 = -v1.

Как отмечалось, система тел называется диссипативной, если ее механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы энергии. В качестве примера рассмотрим диссипацию энергии при абсолютно неупругом прямом центральном ударе двух поступательно движущихся шаров (удар называется абсолютно неупругим, если после удара тела движутся как одно целое, т.е. с одной и той же скоростью).

Общая скорость обоих шаров после удара по закону сохранения импульса равна:

(3.20)

Если шары движутся в горизонтальной плоскости, то их потенциальная энергия Еn остается неизменной. Полная механическая энергия системы до удара

После удара она будет равна

Найдем изменение полной механической энергии системы в результате неупругого удара:

Таким образом, при неупругом ударе полная механическая энергия системы уменьшается, т.е. часть ее рассеивается на деформацию соударяющихся тел. На деформацию тел затрачивается работа, равная убыли полной механической энергии системы:

Если второе тело до удара было неподвижно (v2 = 0), то

(3.21)

Неупругий удар на практике применяется для целей двоякого рода. Во-первых, для изменения формы тела – ковки и штамповки металла, раздробления тел. В этом случае важно, чтобы возможно большая часть кинетической энергии первого тела затрачивалась на работу деформации (формула (3.21)), т.е. чтобы масса неподвижного тела m2(например, наковальни вместе с куском металла) была во много раз больше массы ударяющего тела m1 (например, молота).

Вторая цель состоит в перемещении тел после удара и преодолении при этом сопротивлений (забивка свай в землю, вбивание клиньев и т.п.). В этом случае выгодно, чтобы работа, затрачиваемая на деформацию, была как можно меньше и

чтобы общая кинетическая энергия обоих тел после удара 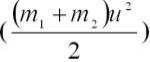была наибольшей. Для этого необходимо, чтобы масса ударяющего тела m1 (молота) была во много раз больше массы второго тела m2 (сваи, гвоздя).

4) Закон сохранения момента количества движения

Из основного уравнения динамики вращательного движения следует, что

Для замкнутой (изолированной) системы результирующий вектор момента всех внешних сил, действующих на тело, равен нулю и

или

Это утверждение представляет собой содержание закона сохранения момента количества движения: и формулируется следующим образом: если результирующий

момент всех внешних сил относительно неподвижной оси вращения тела равен нулю, то момент импульса относительно этой оси не изменяется в процессе движения. Этот закон может быть обобщен на любую незамкнутую систему тел, если результирующий момент всех внешних сил, приложенных к системе, относительно какой-либо неподвижной оси тождественно равен нулю, то момент импульса системы относительно той же оси не изменяется с течением времени.

5) Основной закон динамики вращательного движения твердого тела

Основной закон динамики вращательного движения можно получить из второго закона Ньютона для поступательного движения твердого тела

где – сила, приложенная к телу массой m; а – линейное ускорение тела.

Если к твердому телу массой m в точке А (рис. 5) приложить силу , то в результате жесткой связи между всеми материальными точками тела все они получат угловое ускорение и соответственные линейные ускорения, как если

бы на каждую точку действовала сила ,…, . Для каждой материальной точки можно записать:

,

где ,

Рис. 5. Твердое тело, вращающееся под действием силы около оси “ОО”.

где mi – масса i-й точки; – угловое ускорение; ri – ее расстояние до оси вращения.

Умножая левую и правую части уравнения (1.7) на ri, получают

где – момент силы – это произведение силы на ее плечо ri.

Плечом силы называют кратчайшее расстояние от оси вращения “ОО” (рис. 5) до линии действия силы .

– момент инерции i-й материальной точки.

Выражение (1.8) можно записать так:

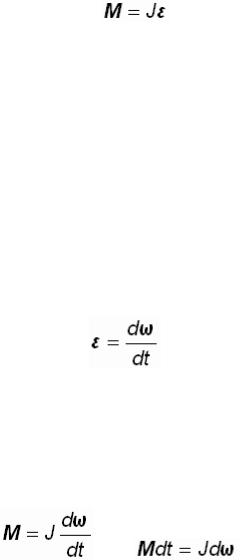
Просуммируем левую и правую части (1.9) по всем точкам тела:

.

Обозначим 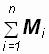через М, а через J, тогда

Уравнение (1.10) – основной закон динамики вращательного движения твердого

тела. Величина – геометрическая сумма всех моментов сил, то есть

момент силы F, сообщающий всем точкам тела ускорение . – алгебраическая сумма моментов инерции всех точек тела. Закон формулируется так: “Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение”.

Мгновенное значение углового ускорения , есть первая производная угловой скорости 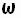по времени t , то есть

где – элементарное изменение угловой скорости тела за элементарный промежуток времени dt.

Если в выражение основного закона (1.10) поставить значение мгновенного ускорения (1.11), то

где – импульс момента силы – это произведение момента силы М на промежуток времени dt .

– изменение момента импульса тела,

– момент импульса тела есть произведение момента инерции J на угловую скорость , а есть dL.

Поэтому основной закон динамики вращательного движения твердого тела формулируется так: “Импульс момента силы , действующий на вращательное тело, равен изменению его момента импульса dL”:

или = dL.

6) смотреть Лекции Турикова.

7) Деформация называется упругой, если после прекращения действия внешних сил тело принимает

первоначальные размеры и форму. Деформации, которые сохраняются в теле после прекращения действия внешних сил, называются пластическими (или остаточными). Деформации реального тела всегда пластические, так как они после прекращения действия внешних сил никогда полностью не исчезают. Однако если остаточные деформации малы, то ими можно пренебречь и рассматривать упругие деформации, что мы и будем делать.

В теории упругости доказывается, что все виды деформаций (растяжение или сжатие, сдвиг, изгиб, кручение) могут быть сведены к одновременно происходящим деформациям растяжения или сжатия и сдвига.

Рассмотрим однородный стержень длиной l и площадью поперечного сечения S (рис. 34), к концам которого приложены направленные вдоль его оси силы F1 иF2 (F1=F2=F), в результате чего длина стержня меняется на величину l. Естественно, что при растяжении l положительно, а при сжатии отрицательно.

Сила, действующая на единицу площади поперечного сечения, называется напряжением:

(21.1)

Если сила направлена по нормали к поверхности, напряжение называется нормальным, если же по касательной к поверхности — тангенциальным.

Количественной мерой, характеризующей степень деформации, испытываемой телом, является его относительная деформация. Так, относительное изменение длины стержня (продольная деформация)

(21.2)

относительное поперечное растяжение (сжатие)

где d — диаметр стержня.

Деформации и ' всегда имеют разные знаки (при растяжении l положительно, a d отрицательно, при сжатии l отрицательно, a d положительно). Из опыта вытекает взаимосвязь и ':

где — положительный коэффициент, зависящий от свойств материала и называемый коэффициентом

Пуассона*.

Английский физик Р. Гук (1635—1703) экспериментально установил, что для малых деформаций относительное удлинение и напряжение прямо пропорциональны друг другу:

(21.3)

где коэффициент пропорциональности Е называется модулем Юнга**. Из выражения (21.3) видно, что модуль Юнга определяется напряжением, вызывающим относительное удлинение, равное единице.

Из формул (21.2), (21.3) и (21.1) вытекает, что

Деформацию сдвига проще всего осуществить, если взять брусок, имеющий форму прямоугольного параллелепипеда, и приложить к нему силу F , (рис. 36), касательную к его поверхности (нижняя часть бруска закреплена неподвижно). Относительная деформация сдвига определяется из формулы

где s — абсолютный сдвиг параллельных слоев тела относительно друг друга; h — расстояние между слоями (для малых углов tg ).

8) Гармонические Колебания

Механическое гармоническое колебание - это прямолинейное неравномерное движение, при котором координаты колеблющегося тела (материальной точки) изменяются по закону косинуса или синуса в зависимости от времени.

Согласно этому определению, закон изменения координаты в зависимости от времени имеет вид:

где wt - величина под знаком косинуса или синуса; w- коэффициент, физический смысл которого раскроем ниже; А - амплитуда механических гармонических колебаний.

Уравнения (4.1) являются основными кинематическими уравнениями механических гармонических колебаний.

Рассмотрим следующий пример. Возьмем ось Ох (рис. 64). Из точки 0 проведем окружность с радиусом R = А. Пусть точка М из положения 1 начинает двигаться по окружности с постоянной скоростью v (или с постоянной угловой скоростью w, v = wА). Через некоторое время t радиус повернется на угол ф: ф=wt.

При таком движении по окружности точки М ее проекция на ось х Мх будет совершать движение вдоль оси х, координата которой х будет равна х = А • cos ф = = А • cos wt. Таким образом, если материальная точка движется по окружности радиусом А, центр которой совпадает с началом координат, то проекция этой точки на ось х (и на ось у) будет совершать гармонические механические колебания.

Если известна величина wt, которая стоит под знаком косинуса, и амплитуда А, то можно определить и х в уравнении (4.1).

Величину wt, стоящую под знаком косинуса (или синуса), однозначно определяющую координату колеблющейся точки при заданной амплитуде, называют фазой колебания. Для точки М, движущейся по окружности, величина w означает ее угловую скорость. Каков физический смысл величины w для точки Мх, совершающей механические гармонические колебания? Координаты колеблющейся точки Мх одинаковы в некоторый момент времени t и (Т +1) (из определения периода Т), т. е. A cos wt = A cos w (t + Т), а это значит, что w (t + Т) - wt = 2ПИ (из свойства периодичности функции косинуса). Отсюда следует, что

Следовательно, для материальной точки, совершающей гармонические механические колебания, величину w можно интерпретировать как количество колебаний за определенный цикл времени, равный 2л. Поэтому величину w назвалициклической (или круговой) частотой.

Если точка М начинает свое движение не из точки 1 а из точки 2, то уравнение (4,1) примет вид:

Величину ф0называют начальной фазой.

Скорость точки Мх найдем как производную от координаты по времени:

Ускорение точки, колеблющейся по гармоническому закону, определим как производную от скорости:

Из формулы (4.4) видно, что скорость точки, совершающей гармонические колебания, изменяется тоже по закону косинуса. Но скорость по фазе опережает координату на ПИ/2 . Ускорение при гармоническом колебании изменяется по закону косинуса, но опережает координату по фазе на п. Уравнение (4.5) можно записать через координату х:

Ускорение при гармонических колебаниях пропорционально смещению с противоположным знаком. Умножим правую и левую части уравнения (4.5) на массу колеблющей материальной точки т, получим соотношения:

Согласно второму закону Ньютона, физический смысл правой части выражения (4.6) есть проекция силы Fx, которая обеспечивает гармоническое механическое движение:

Величина Fx пропорциональна смещению х и направлена противоположно ему. Примером такой силы является сила упругости, величина которой пропорциональна деформации и противоположно ей направлена (закон Гука).

Закономерность зависимости ускорения от смещения, вытекающую из уравнения (4.6), рассмотренную нами для механических гармонических колебаний, можно обобщить и применить при рассмотрении колебаний другой физической природы (например, изменение тока в колебательном контуре, изменение заряда, напряжения, индукции магнитного поля и т. д.). Поэтому уравнение (4.8) называют основным уравнением динамики гармонических колебаний.

Рассмотрим движение пружинного и математического маятников.

Пусть к пружине (рис. 63), расположенной горизонтально и закрепленной в точке 0, одним концом прикреплено тело массой т, которое может перемещаться вдоль оси х без трения. Коэффициент жесткости пружины пусть будет равен k. Выведем тело m внешней силой из положения равновесия и отпустим. Тогда вдоль оси х на тело будет действовать только упругая сила, которая согласно закону Гука, будет равна:

Fyпp = -kx.