волноводы

СЛАЙД 2

Рассмотрим трёхслойный планарный волновод , который состоит из диэлектрических сред. Две параллельные плоскости делят всю область на три части. Одна плоскость проходит через точку a1 и вторая через a2 . Верхний и нижний слои не ограничены вдоль оси . Поскольку все три подобласти однородны вдоль осей и , то диэлектрическая проницаемость изменяется только вдоль оси : . Магнитная проницаемость в рассматриваемых средах постоянна и равна проницаемости вакуума: . Электромагнитная волна распространяется в среднем слое толщиной d.

СЛАЙД 3

Поле в диэлектриках описывается системой уравнений Максвелла:

, , , .

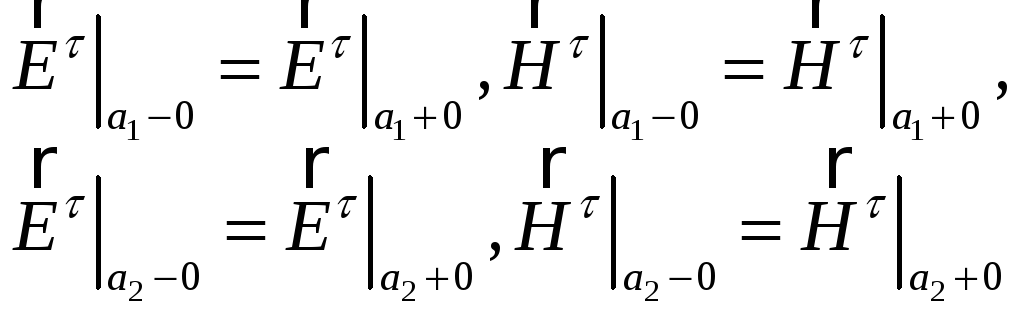
Граничные условия для них состоят из условия равенства тангенциальных компонент на границах разделов сред и условия на бесконечности. Тангенциальными компонентами в нашем случае являются Y и Z компоненты. Условие на бесконечности отражает тот факт , в волноводе нет полей с бесконечной энергией .

СЛАЙД 4

Решение ищется в виде направляемых адиабатических мод. Адиабатические моды это волны , у которых почти вся энергия заключена в некоторой ограниченной области пространства.

СЛАЙД 5

Из геометрии волновода и модели адиабатических мод вытекают следующие соотношения . Применив их можно упростить изначальную систему.

Поскольку производные по равны нулю, то система распадётся на две независимые части, причем в первой системе ненулевыми являются компоненты (TM моды), а во второй (TE моды):

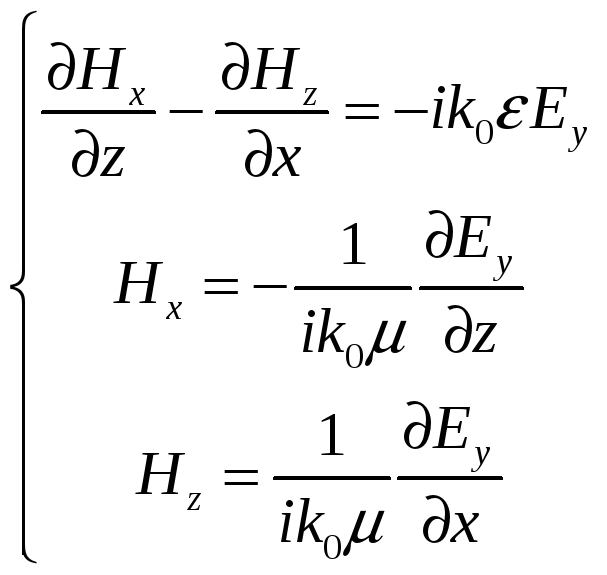
СЛАЙД 5a

Эти две подсистемы соответствуют двум случаям:

• TE (transverse electric) электрический вектор перпендикулярен плоскости падения

• TM (transverse magnetic) магнитный вектор перпендикулярен плоскости падения

СЛАЙД 6

Из полученных систем можно найти волновые уравнения. При этом, их можно выразить либо через поперечные компоненты , либо через продольные компоненты.

В поперечных компонентах сначала находится y компонента и затем через неё выражается z компонента.

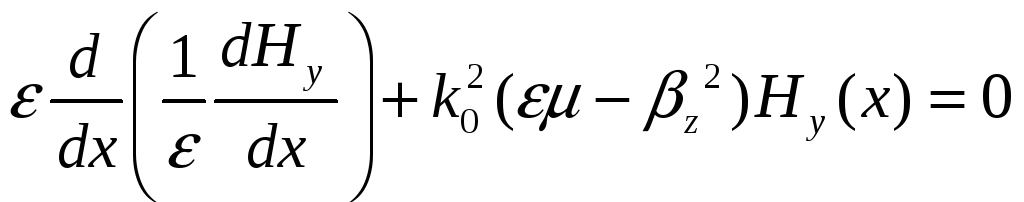
В продольных компонентах наоборот, вначале получают z компоненты

СЛАЙД 7

На данном слайде изображен примерный вид решения для TM моды в продольных координатах. Как видно решение удовлетворяет условиям на бесконечности и на границах разделов сред.

СЛАЙД 8,9

На следующих двух слайдах показаны общие решения волновых уравнений.

В данных решениях присутствуют неопределённые амплитудные коэффициенты и . Чтобы определить эти коэффициенты используют граничные условия.

TM мода в продольных компонентах

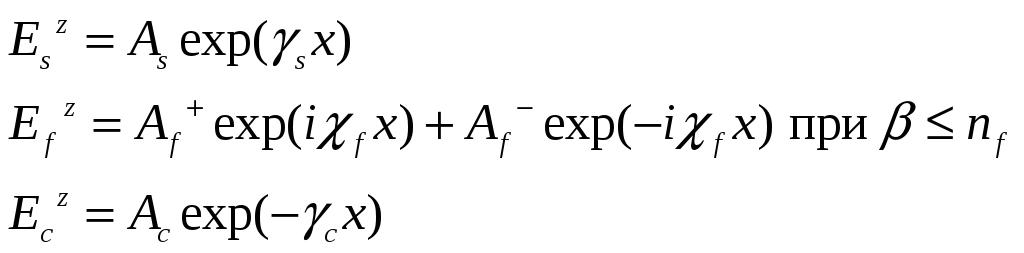
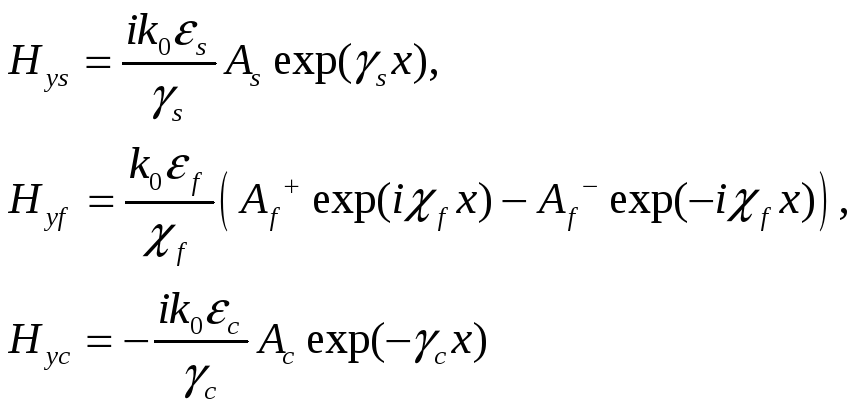
TE мода в поперечных компонентах:

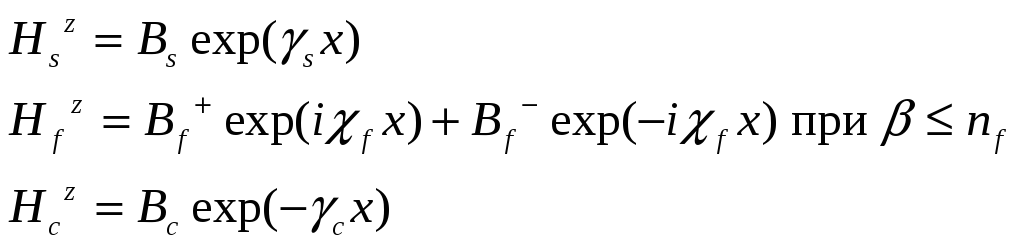
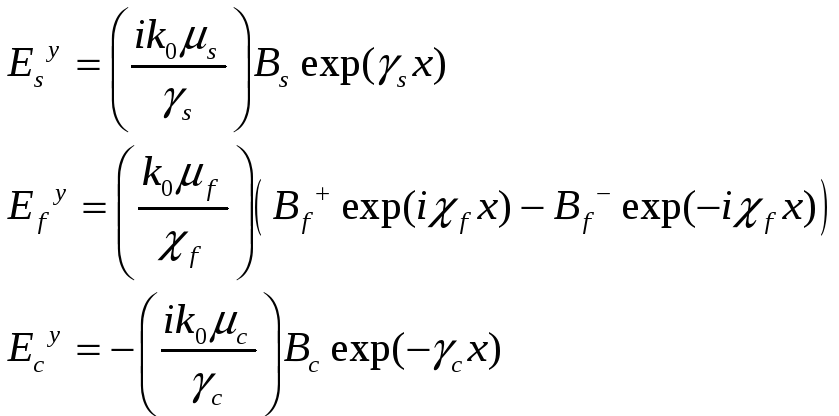
TE мода в поперечных компонентах:

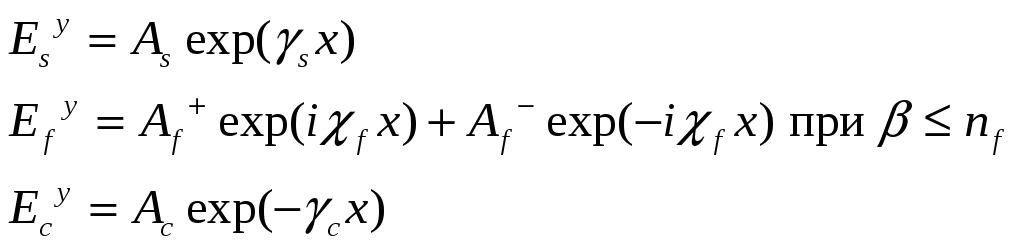
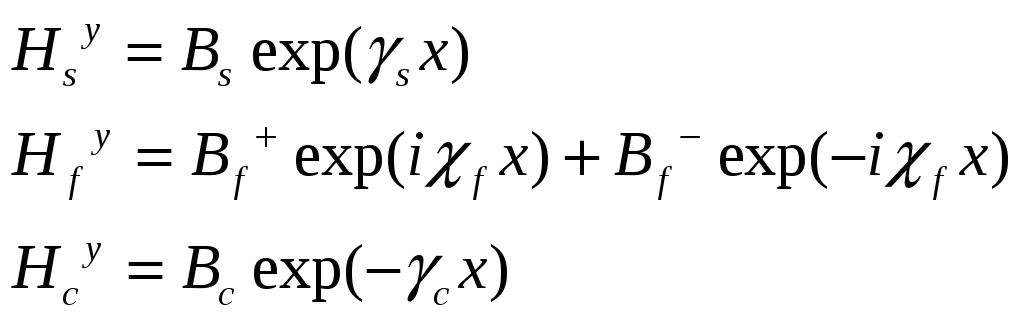
TM мода в поперечных компонентах:

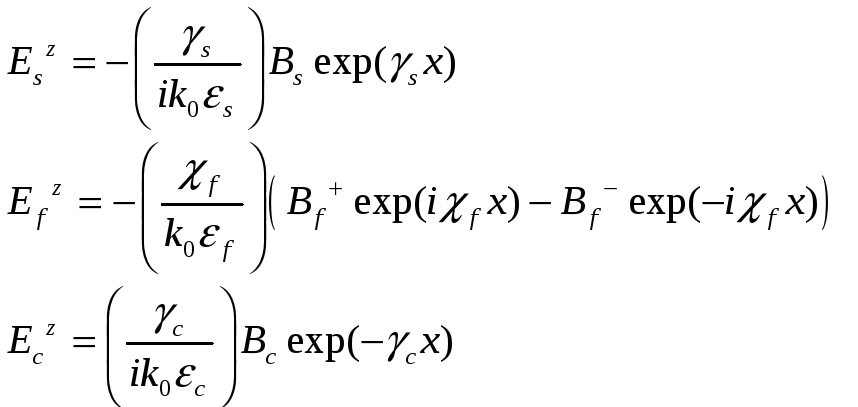
СЛАЙД 10,11

Подставив решения в общем виде в граничные условия получим системы линейных уравнений относительно этих коэффициентов. Параметры изависят от коэффициента фазового замедления .

TM мода в продольных компонентах:

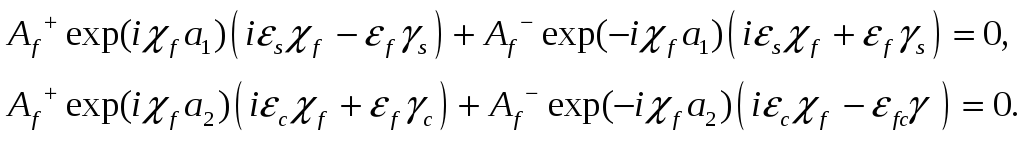
TE мода в поперечных компонентах:

TM мода в поперечных компонентах:

СЛАЙД 12,13

Запишем эти системы в матричном виде. Индексами L (longitudinal) и T (transversal) помечены матрицы в продольных и поперечных координатах.

TE мода в продольных координатах:

TM мода в продольных координатах:

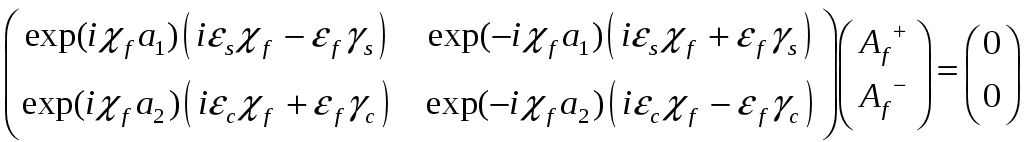
TE мода в поперечных координатах:

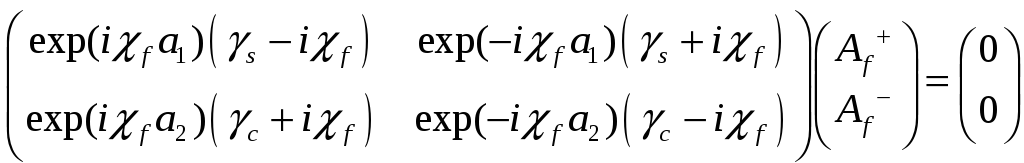
TM мода в поперечных координатах:

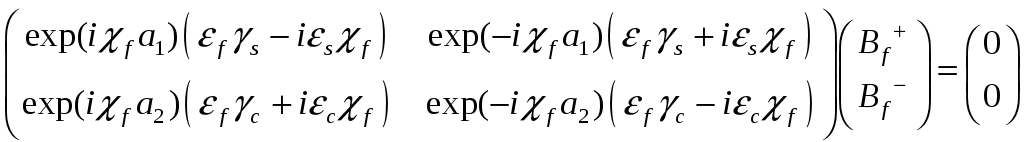
СЛАЙД 14

Коэффициенты полученных систем зависят от параметра и от толщины волноводного слоя h:

При этом не нулевые решения существуют, если определитель системы равен нулю:

Для каждой фиксированной толщины данное уравнение допускает дискретный набор коэффициентов фазового замедления _. Зависимость от толщины называется дисперсионным соотношением.

Решение уравнения ищется при помощи функционала следующего вида:

Для этого используется один из алгоритмов одномерной оптимизации. В данном случае применялись методы нулевого порядка: дихотомии, золотого сечения, прямой перебор, Нелдера-Мида и Хука-Дживса.

СЛАЙД 15

На данном слайде представлен график дисперсионной зависимости. Из графика видно что чем больше толщина , тем больше мод может распространяться в волноводе

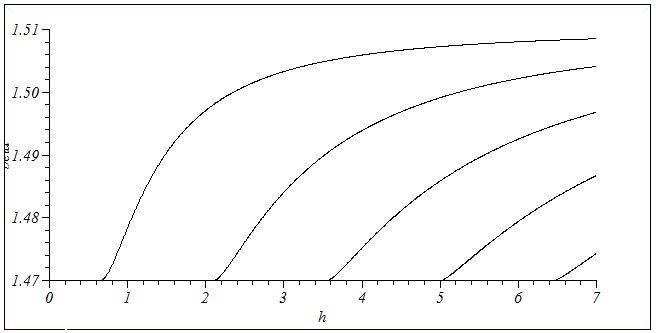
Рис..1 Дисперсионные зависимости для TM мод , H=7 , n_c=1, n_s=1.47

, n_f=1.51.

СЛАЙД 16

З десь изображены графики рассматриваемого функционала .

Рис..2. Графики функционала (3.17) при h=0.6 (сверху слева) , h=1.2 (сверху справа) , h=1.8 (снизу слева) , h=2.4 (снизу справа).

СЛАЙД 17

Сравним различные методы оптимизации в задаче поиска для волновода с толщиной центрального слоя ,, , точность :

Таблица 1.Сравнение методов первого порядка

	Среднее количество итераций
Метод	LTE	LTM	TTE	TTM
дихотомия	21	21	21	21
Золотое сечение	34	34	34	34
перебор	1887301	1935507	1887301	1935373
Нелдера-Мида	109	109	109	109
Хука-Дживса	260	293	260	293

Быстрее всего сходится метод дихотомии. Метод золотого сечения сходится немного медленнее, но для его работы требуется только один параметр - точность, в то время как в дихотомии нужно следить за тем, чтобы шаг был в два раза меньше точности. Алгоритмы Нелдера-Мида и Хука-Дживса предназначены для многомерной оптимизации, и применение их для поиска минимума функций от одной переменной оказывается слишком сложным по сравнению с первыми двумя.

СЛАЙД 18

Решив задачу поиска коэффициента фазового замедления, мы получаем набор дисперсионных зависимостей . Используя их для расчёта элементов матрицы, можно получить систему, имеющую не нулевые решения.

Элементы матриц и амплитудные коэффициенты представляют собой комплексные числа, для поиска решений системы вводится функционал следующего вида:

Чтобы обеспечить устойчивость функционал привязывается к решениям, найденным при других значениях параметров волновода. Например, сначала находится решение при толщине равной , теперь при вычислении функционала для толщины нужно, чтобы разница между новым решением и старым уменьшалась при уменьшении величины шага . Таким образом, функционал приводится к следующему виду:

Для минимизации данного функционала было использовано два алгоритма численной оптимизации: симплекс метод Нелдера-Мида и метод Хука-Дживса. Оба эти метода имеют нулевой порядок, т.е. при работе они опираются непосредственно на значения функции и вычисление производных не требуется. Данные алгоритмы предназначены для минимизации функций с действительными аргументами, поэтому для программной реализации двумерный вектор комплексных амплитуд заменялся соответствующим четырёхмерным вектором:

СЛАЙД 19

Если подставить найденные амплитудные коэффициенты в формулы для общих решений, то можно получить конкретный вид мод.

Рис..3 Амплитуды 1-й, 2-й,3-й и 4-й TM мод, Н=7, n_c=1, n_s=1.47

, n_f=1.51.

СЛАЙД 19

Сравним методы в Хука-Дживса и Нелдера-Мида:

Таблица 2. Сравнение методов многомерной оптимизации, точность .

метод	Хука-Дживса		Нелдера-Мида
	Среднее количество итераций	Среднее значение невязки	Среднее количество итераций	Среднее значение невязки
LTE	1184	4,239826E-15	554	4,615299E-15
LTM	1502	3,671270E-15	582	4,689009E-15
TTE	1030	4,355998E-15	550	4,789500E-15
TTM	1488	3,8627429E-15	575	4,706221E-15

В таблице приведены результаты программной реализации методов в среде DELPHI 2010. В качестве итераций было взято количество вызовов функции, которая вычисляет значение функционала. Метод Нелдера-Мида сходится быстрее, при этом количество итераций для всех случаев приблизительно одинаково, при этом метод Хука-Дживса работает несколько медленнее для TM компонент.

СЛАЙД 21

В задаче поиска КФЗ наиболее эффективным оказывается метод дихотомии, поскольку он имеет наибольшую скорость сходимости среди рассмотренных алгоритмов оптимизации, кроме того данный метод довольно прост в реализации. Методы Нелдера-Мида и Хука-Дживса показали близкие качественные характеристики в задаче поиска амплитудных коэффициентов. В целом метод Нелдера-Мида сходится быстрее и количество итераций при этом изменяется в относительно не больших пределах для разных случаев в отличии от Метода Хука-Дживса.