Математический анализ II Курс Лекций

110 Глава 9. ЧИСЛОВЫЕ РЯДЫ

ряд сходится, если < 1 или = 1 и < 1, и расходится, если > 1 или = 1 и > 1.

I Если 6= 1, то утверждение теоремы следует из признака Даламбера.

теоремы следует из признака Раабе.

Осталось рассмотреть случай, когда = 1, = 1.

Для доказательства расходимости ряда используем лемму (4-ый признак

1

сравнения). Возьмем расходящийся ряд с общим членом (n 1) ln n (этот ряд расходится, потому что его общий член эквивалентен членам последова-

ав теореме Гаусса рассматривается асимптотическое представление

< 1 или = 1, а > 1, и расходится, если = 1 и 6 1. Это утверждение равносильно доказанным теоремам.

Следовательно, признак Даламбера не может решить вопрос о сходимости

Ряд сходится. -

1

Пример 5. Исследовать ряд X (2n 1)!! 1 4 7 (3n 2) на сходи- n! 5 11 16 (6n 1)

мость.

1

, Находим отношение

Признак Даламбера неприменим. Представим полученное отношение в виде:

откуда по признаку Гаусса следует, что ряд расходится. -

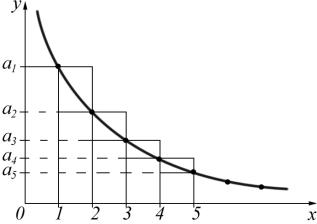
Теорема 9.1.5 (Интегральный признак Коши). Пусть даны

1

X

a) ряд an, (an > 0), причем последовательность fang — убывающая.

n=1

b)функция f (x), определенная на промежутке [1; 1), положительная

иубывающая на этом промежутке, причем f (n) = an, n 2 N.

1

X

Тогда ряд an сходится или расходится одновременно с несобствен-

n=1

k

Теперь просуммируем последнее неравенство по k от k = 1 до k = n. Получим

следовательно, любая частичная сумма ряда будет ограничена: Sn+1 6 I + a1 и ряд сходится.

Интеграл сходится, следовательно, ряд тоже сходится. Оценим скорость сходимости ряда:

-

1

Пример 7. Оценить частичную сумму гармонического ряда X 1 .

n=1 n

, Известно, что этот ряд расходится. Оценим его частичную сумму:

ln (n + 1) 6 Sn 6 1 + ln n. -

§2 Ряды с произвольными членами

2.1 Абсолютная сходимость

1

X

Рассмотрим ряд an, где члены ряда an могут быть как положительны-

n=1

ми, так и отрицательными. Для таких рядов наряду с обычной сходимостью, рассматривается еще абсолютная сходимость.

n=1

Очевидно, что для исследования числового ряда на абсолютную сходимость, можно применить любой из признаков, рассмотренных ранее.

1

X jsin ( n)j, а это означает, что данный ряд сходится абсолютно. - n2

n=1

Теорема 9.2.1. Если ряд сходится абсолютно, то он сходится.

Коши, по " > 0 можно найти такое n0 2 N, что если n > n0, то janj < ".

n

дится (это будет доказано ниже), но не абсолютно. Ряд, составленный из модулей его членов — гармонический ряд. Его расходимость уже была доказана (гл. II, п. 5.1).

Про ряды, которые сходятся, но не абсолютно, иногда говорят, что они

сходятся условно.

2.2 Признаки сходимости рядов с произвольными членами

1

Теорема 9.2.2 (Признак Лейбница). Пусть дан ряд X( 1)n 1 an, где

n=1

an > 0, причем последовательность fang — невозрастающая и lim an = 0.

n!1

1

Тогда ряд X( 1)n 1 an сходится.

n=1

I Рассмотрим частичную сумму ряда

S2m = a1 a2 + a3 a4 + + a2m 1 a2m:

Группируя слагаемые следующим образом:

S2m = (a1 a2) + (a3 a4) + + (a2m 1 a2m) ;

и замечая, что разности в каждой скобке неотрицательны, получим, что последовательность S2m неубывающая.

С другой стороны, группируя эти же слагаемые иначе:

S2m = a1 (a2 a3) (a4 a5) (a2m 2 a2m 1) a2m;

116 Глава 9. ЧИСЛОВЫЕ РЯДЫ

и, замечая, что разности в каждой скобке неотрицательны, получим, что последовательность S2m ограничена сверху: S2m 6 a1.

Следовательно, последовательность S2m имеет предел. Обозначим этот предел через S. Тогда

lim S2m+1 = lim (S2m + a2m+1) = S + 0 = S:

m!1 m!1

Значит lim Sn = S и ряд сходится. J

n!1

Ряд, о котором говорится в теореме, называется знакочередующимся рядом, так как знаки двух соседних членов ряда различны.

вающая; 2) lim 1 = 0. Следовательно, ряд сходится. Абсолютной сходимости

n!1 n

1

здесь нет, т.к. ряд, составленный из модулей X 1 расходится. Следователь-

n=1 n

но, данный ряд сходится условно. -

Замечание 2. Из доказательства теоремы легко получить оценку для суммы такого ряда: S 6 a1. Если применить эту оценку к остатку знакочередующегося ряда (остаток тоже является знакочередующимся рядом), то получим неравенство: jRnj < jan+1j, которое удобно применять при приближенных вычислениях.

Для доказательства монотонного убывания предположим, что аргумент функции f (n) = lnnn меняется на промежутке [2; +1). Тогда эту функцию

можно исследовать на монотонность с помощью методов дифференциального

исчисления. f0 (n) = 1 ln n. Отсюда, если n > 3, то f0 (n) < 0, следователь- n2

но, последовательность модулей членов ряда, начиная со второго, убывающая и ряд сходится.

Для определения нужного количества первых членов ряда воспользуемся

т.е. jR647j < 0; 01. Значит для достижения заданной точности нужно взять

частичную сумму S647 = a2 + + a647, т.е. первые 646 членов ряда. -

1

Пример 4. Исследовать на сходимость ряд X( 1)n lnnn.

n=2

, Ряд знакочередующийся, причем an = lnnn ! 1. Ряд расходится, так как не выполнено необходимое условие сходимости. В этом примере нельзя ссылаться на невыполнение условия теоремы Лейбница, так как эта теорема является только достаточным условием сходимости ряда. -

k=1

2) последовательность fbng убывающая и стремится к нулю.

1

X

Тогда ряд akbk сходится.

k=1

n+`

X

I Рассмотрим сумму akbk и применим к ней преобразование Абеля (гл. 6,

k=n

п. 7.2):

=n

XX

В последнем выражении модули можно отбросить, так как по условию

теоремы должно быть bn+i > bn+i+1 > 0.

` 1

X

Далее, заметим, что (bn+i bn+i+1) + bn+` = bn, и, так как lim bn = 0,

n!1

i=0

Пусть теперь 0 < 6 1. Воспользуемся признаком Дирихле, полагая в

1 нем ak = sin (2k) и bk = k .

Найдем сумму

nn

Отсюда следует, что для всякого n 2 N будет выполняться неравенство

нулю. Следовательно, ряд сходится.

Докажем, что в этом случае нет абсолютной сходимости ряда. Очевидно

следовательно, при отрицательных значениях ряд расходится. -