Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный университет информационных технологий, механики и оптики

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2014 Модуль 3 Tipovik_III_LAST11

.pdf

Скачиваний:

Добавлен:

14.04.2015

Размер:

4.7 Mб

Скачать

☆

1 / 71 2 3 4 5 6 7 > Следующая >>>

Типовой расчет по математике

Интегрирование функции одной переменной

3 модуль

Учебно-методическое пособие

Санкт-Петербург

2014

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

САНКТ-ПЕТЕРБУРГСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ

Брылевская Л.И., Бодрова Н.А., Далевская О.П.,

Сейферт И.В., Сытенко Н.В.

Типовой расчет по математике

Интегрирование функции одной переменной

3 модуль

Учебно-методическое пособие

Санкт-Петербург

2014

Брылевская Л.И., Бодрова Н.А., Далевская О.П., Сейферт И.В., Сытенко Н.В.

Типовой расчет “Интегрирование функции одной переменной”. 3

модуль. Учебно-методическое пособие. – СПб: НИУ ИТМО, 2014. – 75 с.

Предлагаемое пособие предназначено для студентов технических специальностей первого курса.

Рекомендовано к печати Ученым советом естественнонаучного факультета, 22.06.2013, протокол №5.

В 2009 году Университет стал победителем многоэтапного конкурса, в результате которого определены 12 ведущих университетов России, которым присвоена категория «Национальный исследовательский университет». Министерством образования и науки Российской Федерации была утверждена Программа развития государственного

образовательного учреждения высшего профессионального образования «Санкт-Петербургский государственный университет информационных технологий, механики и оптики» на 2009–2018 годы.

Санкт-Петербургский национальный исследовательский Университет информационных технологий, механики и оптики, 2013

Брылевская Л.И., Бодрова Н.А., Далевская О.П., Сейферт И.В., Сытенко Н.В. 2014

Оглавление
Часть I. МЕТОДИЧЕСКИЕ УКАЗАНИЯ.....................................................................................................						4
Раздел 1. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ.............................................................................................						4
	Задание 1. Интегрирование методом внесения под знак дифференциала.					........................... 5
	Задание 2. Нахождение интегралов вида			sin x	cos xdx , ........................................... 5
				Mx	N
	Задание 3. Нахождение интегралов вида			ax2	bx c dx ,
	Mx	N
			dx ....................................................................................................................			8
	ax2	bx c
	Задание 4. Интегрирование дробно-рациональных функций ................................................					10
	Задание 5. Интегрирование иррациональных функций вида
	R		......................................................................................			15
	Задание 6. Интегрирование иррациональных функций вида R x, a2					x 2 ,
	R x, x2	a2 , R x, a2 x2 ......................................................................................				17
	Задание 7. Интегрирование тригонометрических функций R (sin x, cos x) методом
	подстановки. ................................................................................................................................					18
Раздел 2. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ ..............................................................................................						21
1.	Методы интегрирования ........................................................................................................					21
	Задание 8. Метод интегрирования по частям в определённом интеграле ...........................					21
	Задание 9. Метод замены переменной в определённом интеграле. ....................................					22
2.	Приложения определённого интеграла................................................................................					23
	Задания 10, 11, 12. Нахождение площади области, ограниченной кривыми, и отыскание
	длины кривой...............................................................................................................................					23
Раздел 3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ ...........................................................................................						40
	Задание 13. Нахождение несобственных интегралов:.............................................................					40
	а) по бесконечному промежутку интегрирования, .................................................................. 40
	б) от неограниченной на отрезке функции.			...........................................................................		401
Часть 2. ТИПОВЫЕ ЗАДАНИЯ..............................................................................................................						44

Часть I. МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Типовой расчѐт содержит 30 вариантов заданий по трѐм разделам интегрального исчисления: «Неопределѐнные интегралы», «Определѐнные интегралы и их приложения» и «Несобственные интегралы». В каждом варианте 15 задач.

Разберѐм решения типовых заданий по каждому из указанных разделов.

Раздел 1. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ

Для выполнения первых трѐх заданий помимо знания таблицы интегралов нам понадобится:

1) свойство линейности неопределѐнного интеграла

(a f (x) b g(x)) dx a f (x) dx b g (x)dx , где a, b R;

2)знание тригонометрических формул и основных свойств элементарных функций;

3)метод интегрирования внесением под знак дифференциала.

По определению дифференциала функции '(x) dx d ( (x)) . Переход в этом равенстве слева направо называют «подведением

множителя		'(x) под знак дифференциала».
Пусть		требуется	найти	интеграл вида	f (	(x)) '(x)dx .	В	этом
интеграле	подведѐм функцию			'(x) под знак дифференциала,			а	затем
выполним	подстановку		(x)	u (замену переменной интегрирования),
тогда мы получим формулу подстановки в неопределѐнном интеграле
		f ( (x))	'(x) dx	f ( (x)) d (	(x))	f (u) du		(1)
С появлением некоторого навыка интегрирования						подстановка		(x) u

обычно производится в уме.

Простой частный случай формулы (1) можно получить для линейной функции (x) ax b , тогда d (ax b) a dx . Следовательно,

f (ax b)dx	1	f (ax b)d (ax b)	1	F (ax b) c
f (ax b)dx	a	f (ax b)d (ax b)	a	F (ax b) c
	a		a	(2)
		4

Задание 1. Интегрирование методом внесения под знак дифференциала.

	Пример 1. Найдите		dx


			4x 1
			4x 1

Решение: Воспользуемся формулой (2), поскольку внутренняя функция

композиции

(x)

1 линейна:

(4x

1) 0,5 d (4x

2(4x 1)0,5

4x 1

С .

Пример 2.

Найдите

(3arctg 4 x

1)dx

1 x2

Решение: Воспользуемся свойством линейности, разобьѐм исходный интеграл на сумму двух интегралов и вынесем константу за знак первого интеграла

3arctg4 x

3 arctg 4 x

1 x2

Второй интеграл табличный, а в первом

внесѐм производную под знак

дифференциала

d (arctgx) , выполним подстановку arctgx t и

1 x2

воспользуемся табличной формулой для интеграла от степенной функции

3 t 4 dt arctgx 3	t 5	arctgx С 3	arctg5 x	arctgx С .

5			5

Задание 2. Нахождение интегралов вида			sin	x cos	x dx ,
cos x cos x dx,	sin xsin	x dx,	sinn x cosm x dx ,			(3)
Для нахождения интегралов	вида sin	x	cos	x dx ,	cos x cos	x dx,

sin x sin x dx следует преобразовать подынтегральную функцию,

воспользовавшись формулами тригонометрии

sin

cos

(sin(

sin(

)x)

cos

(cos(

cos(

)x)

(4)

sin

x sin

(cos(

cos(

)x)

Пример 1. Найдите

Решение. Так как по формуле (4)

, то

Для нахождения интегралов вида используют метод замены переменной (или метод внесения под знак дифференциала) и формулы понижения степени:

Рассмотрим случай, когда хотя бы один показатель степени является нечётным числом. Пусть n = 2k + 1. Тогда

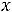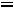
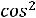
Так как , а , то, обозначив , получим интеграл от рациональной функции:

Отметим, что этот метод интегрирования применим и в случае, когда один из показателей степеней m или n нечѐтное число, а второй – рациональное число.

Если оба показателя степени чётные, то степени необходимо понизить, используя формулы понижения степени (5), известные из курса тригонометрии.

Пусть n 2k , m 2l .Тогда

= .

В полученном интеграле следует раскрыть скобки, воспользоваться свойством линейности (т. е. представить как сумму интегралов) и применять описанные методы до тех пор, пока интеграл не сведѐтся к сумме табличных первообразных.

Рассмотрим оба случая на примерах.

Пример 2. Найдите .

Решение. Так как показатель степени – чѐтное число (n = 4), используем формулу (5) и раскроем скобки:

Полученный интеграл равен сумме трѐх интегралов:

Первые два интеграла будут равны	1	x	и	1	sin 2x	соответственно. В
	4			4

последнем интеграле опять применим формулу понижения степени:

В результате имеем

Пример 3. Найдите

Решение. Заметим, что

степень функции sin x ,

, является

рациональным числом,

а показатель степени cos x

–

нечѐтное число

(m 1) . Значит, можно ввести замену:

Тогда

Задание 3. Нахождение интегралов вида		Mx	N		dx ,

	ax2		bx	c
		Mx	N			dx


		ax2
		ax2	bx	c

(первый интеграл рассмотрим при условии, что квадратный трѐхчлен не

имеет корней, то есть его дискриминант D	0 ).
Метод интегрирования подобных	функций заключается в


следующем. Пользуясь свойством линейности, представим					исходный
интеграл в виде суммы двух интегралов от дробей с					теми же
знаменателями, в	числителе	первой	дроби	будет производная
(ax2 bx c)' 2ax	b , а в	числителе	второй	– единица. Такое

преобразование позволяет свести исходные интегралы к табличным.

Так как

(2ax

, для

первого

второго

интегралов получим следующие разложения

2ax

(6)

ax2

2ax b

(7)

ax2

В первых

интегралах

полученных

сумм (6) и

(7)

достаточно

воспользоваться методом внесения под знак дифференциала или методом

подстановки. Поскольку (2ax

b)dx

d(ax2

c) , обозначим

s = ax2 + bx + c, тогда легко получим табличные интегралы

2ax

ax2

2ax

ax2

2 c

ax2

Выделение полного квадрата в квадратном трѐхчлене ax2 bx

c в

интегралах

также позволяет свести их

ax2

табличным интегралам, посредством замены

dt .

Рассмотрим несколько примеров.

Пример 1. Найдите	(x	8) dx

	x2	4x 20
	x2	4x 20

Решение. Представим интеграл в виде суммы двух интегралов (6), в числителе у первого из них производная знаменателя, а у второго – константа.

8) dx

(2x

4) 12

(2x

4) dx

x2 4x

4x 20 2

4x 20

Выделим полный квадрат в знаменателе дроби под знаком второго

интеграла:			x2	4x	20	(x 2)2	42 . В результате:
	1	d (x2	4x	20)	6	dx		1	ln(x2	4x 20)	3	arctg	x	2	c
2		x2	4x 20			(x 2)2	42 2				2			4

Пример 2.					Найдите								3x	1			dx .


											2x2			x		1
											2x2			x		1
Решение. Найдѐм дифференциал подкоренного выражения:
									d (2x2							x		1)			(4x				1)dx.
Получим 4x						1 в числителе:
													3x		1		3	(4x			1)				1	.
													3x		1	4		(4x			1)				4	.
																4									4
						3x		1		dx			3				4x			1				dx	1						dx


						2x2							4			2x2									4					2x2
						2x2		x 1					4			2x2				x 1					4					2x2			x 1
3							1						dx					3											1						dx
3		2x2			x	1	1						dx					3				2x2				x	1		1						dx


2							4						2	x		1		2											4			2			1	2		7
2							4							x		1		2											4			2				2
								2			x																							x
								2			x			2		2
																																			4			16


Заменим в последнем интеграле																	x			1			t, k		2		7		, dx			dt :
Заменим в последнем интеграле																	x			4			t, k		16				, dx			dt :
																				4					16

				dx									dt																				1				x	1
				dx									dt				ln		t				t 2		k 2			c ln				x	1		x2		x	1	c


					2			2				t	2	k	2																		4			2		2
												t		k																			4			2		2
			1			7
	x


			4			4
			4			4

Таким образом,

1 / 71 2 3 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.11.2018132.48 Кб102-23_сетевые адаптеры.docx
#
21.03.2016669.87 Кб72-задания.pdf
#
20.03.2016172.54 Кб72.doc
#
21.03.2016397.47 Кб92012-10_ES_Razvitie_Innovats_Sistemy__17_str.Pdf
#
22.05.2015637.74 Кб132013 Модуль 4.pdf
#
14.04.20154.7 Mб102014 Модуль 3 Tipovik_III_LAST11.pdf
#
21.03.2016103.72 Кб72014_03_03_-_Java_IO.pdf
#
14.04.201528.67 Кб322014_Lab4_Manual.doc
#
14.04.20151.09 Mб92014_Lab6_Manual.pdf
#
14.04.20151.15 Mб72015UML06.pdf
#
14.04.20151.02 Mб42015UML07.pdf