
(9)2НЕОПР-Й ИНТЕГРА - копия - копия
.pdf
14.5.2. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ
|
|
|
Вид интеграла |
|
|
|
|
|
|
|
|
|
|
|
Метод интегрирования |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) |
Если дробь |
Em |
x |
неправильная (т.е. степень |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
x |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
Pn |
x |
|
|
|
|
|
|
|
|
|
|
|
числителя больше или равна степени знамена- |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Em |
x |
dx |
|
|
|
|
|
|
|
теля: m n ), |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то по правилу деления многочлена |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на многочлен эту дробь всегда можно предста- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вить в виде суммы целой рациональной функции |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и правильной дроби: |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Em |
x |
= M k x |
Rs x |
. |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pn x |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pn x |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
Целая часть |
|
M k x |
интегрируется непосредст- |
||||||||||||||||
|
|
|
|
|
|
Em x |
|
|
|
|
|
|
|
|
венно. Задача свелась к интегрированию пра- |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вильной дроби. |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = |
|
|
|
3) |
Знаменатель |
|
|
правильной |
рациональной |
дроби |
|||||||||||||||||
|
|
|
|
|
|
P x |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
разлагают на множители первой степени (х – а) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
||||||||||||||||||||
|
|
M k |
|
x dx |
|
Rs |
dx |
|
(некоторые из них могут повторяться) и множи- |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Pn |
x |
тели второй степени x2 px q , не имеющие |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
действительных корней (т.е. дискриминант |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
меньше нуля); некоторые из этих множителей |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
также могут повторяться. |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Rs x |
|
|
|
|
|
|
4) |
Если |
|
знаменатель |
правильной рациональной |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
Rs |
x |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Pn x |
|
|
|
|
|
|
|
дроби |
|
|
|
|
|
|
|
|
разлагается на множители |
вида |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Rs x |
|
|
|
|
|
|
|
|
|
|
|
Pn |
|
|
|
|
|
|
|
|
||||||||||
x a x b . . . x m |
|
Pn x x a x b . . . (x m) , |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
A |
|
|
|
|
|
B |
|
|
|
|
|
M |
|
|
|
|
то каждому |
|
|
множителю |
соответствует |
дробь |
||||||||||||||||
= |
|
+ |
|
|
|
|
+ . . . + |
. |
|
|
|
|
|
|
|
A |
|
|
|
|
B |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
x a |
|
|
|
|
x b |
|
|
x m |
|
|
|
|
вида |
|
|
, |
|
|
|
и т.д. |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x a |
|
|
x b |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
145

Пример. |
Rs |
x |
= |
|
|
|
|
|
|
|
|
|
|
|
5) |
|
|
Знаменатель |
содержит |
только |
множители |
|||||||||||||||||||||||||||||
Pn |
x |
|
|
|
|
|
|
|
|
|
|
|
|
первой степени, но некоторые из них повторя- |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Rs x |
|
|
|
|
|
|
|
|
|
ются, |
|
|
|
|
|
|
|
|
например: |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pn x x a k x b n . . . (x m) . |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
x b x с |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x a |
|
|
|
|
|
|
Тогда каждому множителю вида x a k соот- |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
|
A2 |
|
A3 |
|
|
ветствует следующая сумма дробей: |
|
||||||||||||||||||||||||||||||
|
x a 3 |
|
|
|
x a 2 |
x a |
|
|
|
|
|
|
A1 |
|
A2 |
|
|
Ak |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. . . |
|
. |
|
|
|||||||
|
|
|
|
|
|
|
B |
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x a k |
x a k 1 |
x a |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x b |
x c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Пример. |
|
Rs x |
= |
|
|
|
|
|
|
|
|
|
|
6) |
|
Знаменатель правильной дроби содержит мно- |
||||||||||||||||||||||||||||||||||
|
Pn |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
жители второй степени x px q . Каждому та- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Rs x |
|
|
|
|
|
|
|
|
|
кому множителю соответствует правильная дробь |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A x B |
|
|
|
|
|
|
|
|||||||||||||||||||
(x2 px q) x2 rx s |
вида |
|
. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x2 px q |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Ax B |
|
|
|
|
|
|
|
|
|
Cx D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
x2 px q |
x2 rx s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Rs |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
7) |
|
Некоторые множители второй степени повто- |
|||||||||||||||||||||
Пример. |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
px q k . Каждому такому |
|||||||||||||||||||||||||
|
|
P |
|
x |
|
|
|
|
|
|
|
|
|
ряются, например, |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Rs |
|
|
|
|
|
|
|
|
множителю |
соответствует |
сумма |
дробей: |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
A1 x B1 |
|
|
|
|
A2 x B2 |
|
||||||||||||||||||||||||||||||||||||
(x2 px q)2 (x2 rx s) |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.. |
||
|
|
|
|
|
|
|
A1 x B1 |
|
|
|
|
|
A2 x B2 |
|
|
|
|
|
|
|
|
k |
|
|
|
|
k 1 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
px q |
|
|
x |
2 |
px q |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
x 2 px q 2 |
x 2 px q |
|
|
|
|
Ak x Bk |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Cx D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 px q |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
x 2 rx s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
8) Неизвестные коэффициенты разложения А, В, С и т.д. можно находить двумя способами.
Первый способ (метод неопределённых коэффициентов или по другому - метод сравнения коэффициентов). Он состоит в сле-
дующем.
|
Правильную рациональную дробь |
Rs |
x |
разлагают на сум- |
||
Pn |
x |
|
||||
|
|
|
||||
му простейших (как описано выше);
В правой части этого разложения дроби складывают (при-
водят к общему знаменателю и т. д.), получают также правильную дробь, после чего знаменатели левой и правой частей (а они одинако-
вые!) отбрасывают.
146

Получают тождественное равенство, в левой части кото-
рого стоит многочлен с известными коэффициентами, а в правой
части стоит многочлен с неизвестными коэффициентами. Приравнивая
коэффициенты многочленов при одинаковых степенях х, получим ли-
нейную систему из n уравнений c n неизвестными. Решив её, найдём искомые коэффициенты.
Второй способ (метод частных значений).
В полученное тождественное равенство двух многочленов под-
ставляют конкретные числовые значения x . Этим самым вновь получают систему линейных уравнений, из которых и найдутся неизвестные коэффициенты разложения. Для простоты вычисле-
ний удобнее придавать переменной x значения, при которых знаменатель правильной дроби обращается в нуль (т.е. значения корней знаменателя Pn x ).
Замечание. В практических вычислениях нередко применяют комби-
нированный прием, т.е. для определения одних коэффициентов приме-
няют первый способ, других – второй.
Пример. Рациональную дробь |
|
2x |
разложить на сумму |
|||
|
|
|
|
|||
x2 |
1 2 |
x 1 |
||||
|
|
|||||
простейших.
Решение. Дробь правильная, множитель x2 1 не имеет действительных корней (т.е. не разлагается на множители), следовательно, разложение имеет вид:
2x |
|
Ax B |
|
Cx D |
|
E |
|
|
= |
|
|
|
. |
||
x2 1 2 x 1 |
x2 1 2 |
x2 1 |
x 1 |
||||
Коэффициенты А, В, С, D, E подлежат определению.
Приводя к общему знаменателю и отбросив его, получаем:
2x Ax B x 1 Cx D x2 1 x 1 E x2 1 2
или, после очевидных преобразований,
147

2x C E x4 C D x3 A C D 2E x2
A B C D x B D E
Приравнивая коэффициенты многочленов, стоящих в левой и
правой частях тождества, приходим к системе:
х4 |
0 C E |
х2 |
0 A C D 2E |
х0 |
0 B D E |
х3 |
0 C D |
х1 |
2 A B C D |
|
|
|
|
|
|
|
|
Решив систему, получаем: A 1; B 1; C 12 ;D 12 ;E 12
.
|
2x |
|
x 1 |
|
0,5x 0,5 |
0,5 |
|
|
Следовательно, |
|
= |
|
|
|
|
|
. |
x2 1 2 x 1 |
x2 1 2 |
x2 1 |
x 1 |
|||||
15.5.4. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНОСТЕЙ
|
m |
|
r |
|
|
|
|
|
|
||
|
n |
,. . . x |
s |
dx |
|
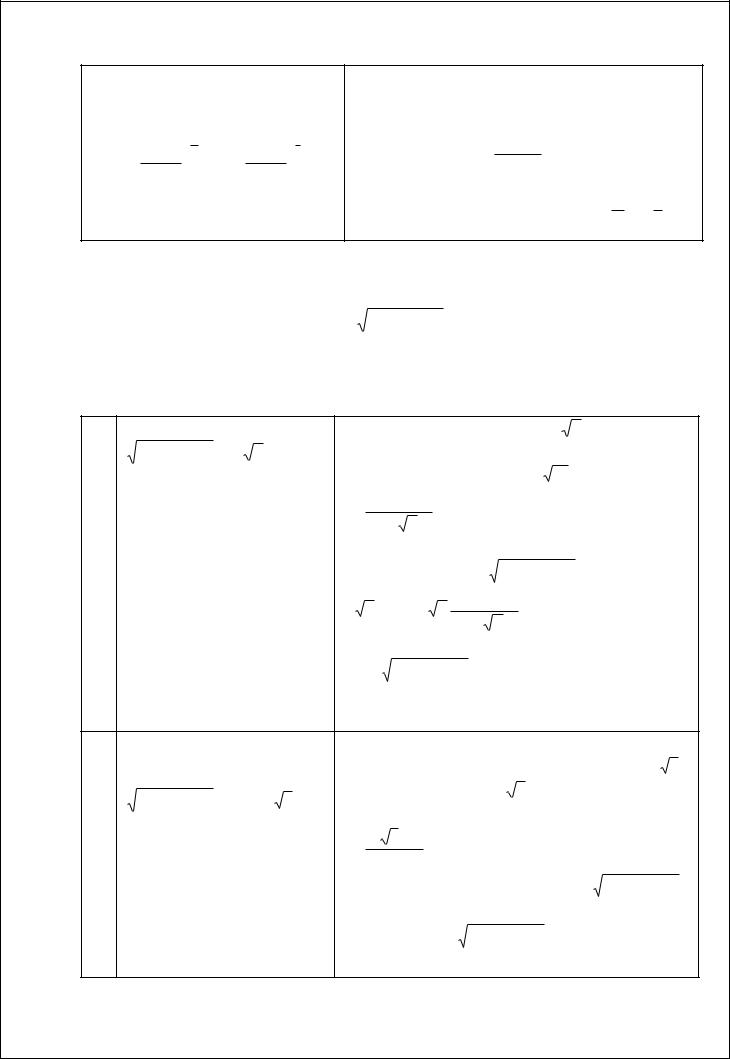
1) R x,x |
|
|
|
||
|
|
|
|
|
|
Буква R означает, что над величинами
m r
производятся рациональные действия: сложение, вычитание, умножение (в том числе на постоянный множитель), возведение в целую степень (как положительную, так и отрицательную), деление.
Интегрирование таких выражений при-
водится к интегрированию рациональных функций с помощью подстановки:
x t k ,
где к – общий знаменатель дробей
mn , . ., rs .
148
|
|
|
|
|
|
Приводится к интегрированию рациональ- |
||||||||||
2) |
|
|
|
|
|
ной функции заменой |
|
|
|
|
||||||
|
|
m |
|
r |
|
|
|
|
|
|
ax b |
k |
|
|
|
|
|
ax b n |
ax b s |
|
|
|
|
|
|
cx d t , |
|
|
|||||
R x, |
|
, . . . , |
|
|
dx |
|
|
|
|
|
|
|||||
|
cx d |
cx d |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m , . ., |
r . |
|
|
|
|
|
|
к – общий знаменатель дробей |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
s |
14.5.5. |
ИНТЕГРИРОВАНИЕ КВАДРАТИЧНЫХ ИРРАЦИОНАЛЬНОСТЕЙ |
|||||||||||||||
|
|
|
|
|
|
R x, ax2 bx c dx |
|
|
|
|
|
|
||||
|
|
|
|
ПОДСТАНОВКИ ЭЙЛЕРА |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Для определённости перед |
|
a возьмём |
||||||||
1. |
ax2 bx c |
a x t , |
знак плюс. |
|
|
|
|
|
|
|
|
|||||
|
если а >0 |
|
|
Тогда |
ax2 bx c ax2 |
2 a x t t 2 , отсюда |
||||||||||
|
|
|
|
|
|
x |
t 2 c |
- рациональная функция от t, |
||||||||
|
|
|
|
|
|
b |
2 a t |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
(значит рациональной функцией будет и dx |
||||||||||
|
|
|
|
|
|
), следовательно, |
ax2 bx c |
|
|
|||||||
|
|
|
|
|
|
a x t |
a |
t 2 c |
t . |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
b 2 |
a t |
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, интеграл |
|
|
|
|
||||||
|
|
|
|
|
|
R x, |
ax2 bx c dx преобразуется в инте- |
|||||||||
|
|
|
|
|
|
грал от рациональной функции от t. |
|
|||||||||
|
|
|
|
|
|
Возводя в квадрат обе части, получаем (для |
||||||||||
|
|
|
|
|
|
определённости взяли знак плюс перед |
с ): |
|||||||||
2. |
ax2 bx c = x t c , |
|
ax2 bx c = x2t 2 2xt c c . |
Отсюда х оп- |
||||||||||||
|
ределяется как рациональная функция от t: |
|||||||||||||||
|
если с>0 |
|
|
|
||||||||||||
|
|
|
|
x 2t |
c b . |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
a t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, и dx и корень |
ax2 bx c |
|||||||||
|
|
|
|
|
|
рационально выражаются через t , значит, |
||||||||||
|
|
|
|
|
|
интеграл R x, |
ax2 |
bx c dx сведён к инте- |
||||||||
|
|
|
|
|
|
гралу от рациональной функции от t. |
|
|||||||||
|
|
|
|
|
|
|
149 |
|
|
|
|
|
|
|
|
|
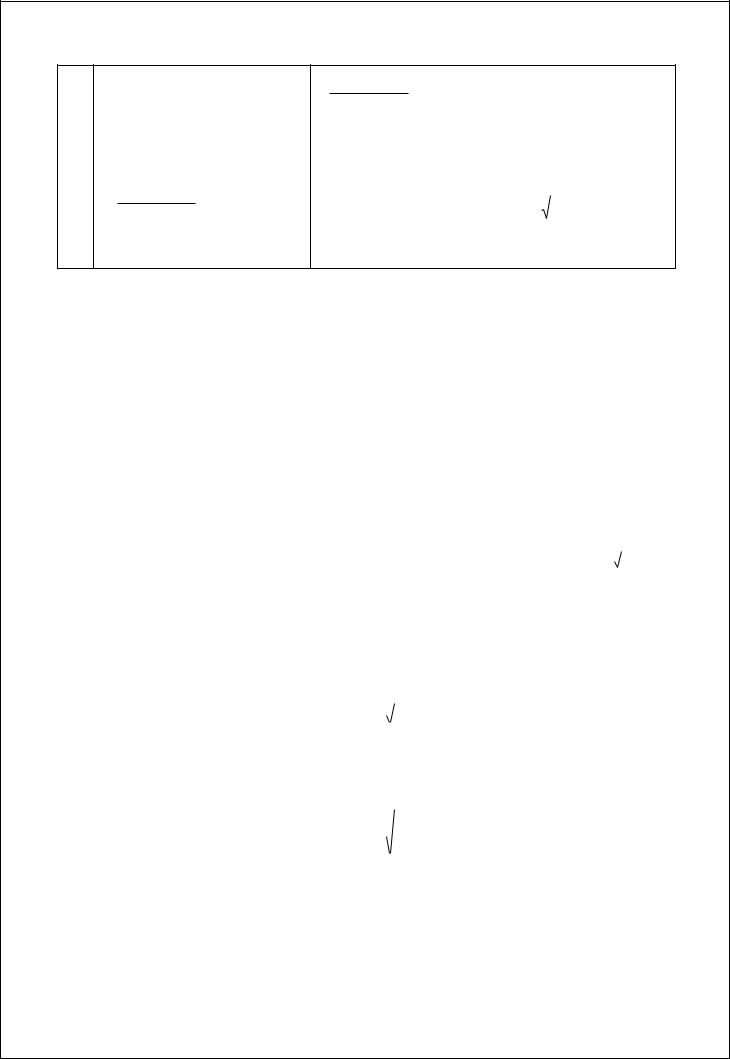
3.Пусть , - действи-
тельные различные корни трёхчлена ax2 bx c
.
Полагаем

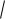 ax2 bx c x t
ax2 bx c x t
Так как ax2 bx c = a x x , то

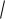 ax2 bx c x t ,
ax2 bx c x t ,
a x x = x 2 t 2 , |
|
|
|
|
a x x t 2 , отсюда x |
a t 2 |
. |
||
|
|
|||
|
|
a t 2 |
||
В результате интеграл R x, |
|
|
dx |
|
|
ax2 bx c |
|||
преобразуется в интеграл от рациональной функции
ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ БИНОМОВ
xm a b xn p dx .
Здесь a, b - произвольные постоянные, m, n, p – рациональные числа. Такие интегралы сводятся к интегралам от рациональной функции в следующих трёх случаях (применяя подстановки П.Л. Чебышева):
|
|
|
|
|
|
|
|
Выполняют |
подстановку t k x , |
||||||
1. |
Когда |
|
р – целое число (по- |
где k-общий знаменатель дробей |
|||||||||||
|
ложительное, отрицательное |
m, n. В результате приходят к ин- |
|||||||||||||
|
или нуль) |
|
|
|
тегралу от рациональной функ- |
||||||||||
|
|
|
|
|
|
|
|
ции. |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
2. |
Когда |
m 1 |
– целое число (по- |
Интегрируется путём подстановки |
|||||||||||
|
|
n |
|
t k |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
a bxn , |
где |
k - знаменатель |
|||||||
|
ложительное, отрицательное |
дроби |
р. Получают интеграл от |
||||||||||||
|
или нуль) |
|
|
|
|||||||||||
|
|
|
|
рациональной функции. |
|||||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||||
3. |
Когда |
|
m 1 |
p – целое число |
Интегрируется путём подстановки |
||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
t k |
a bxn |
|
|
||||||
|
(положительное, отрицатель- |
|
|
, |
где |
k - знаменатель |
|||||||||
|
xn |
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||
|
ное или нуль) |
дроби |
р ; |
получают интеграл от |
|||||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
рациональной функции |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
150
14.5.6.ИНТЕГРИРОВАНИЕ ВЫРАЖЕНИЙ, СОДЕРЖАЩИХ
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
R sin x ; cos x dx
Здесь буква R, как и выше, означает, что над синусом и косинусом
производятся рациональные операции.
1.
2.
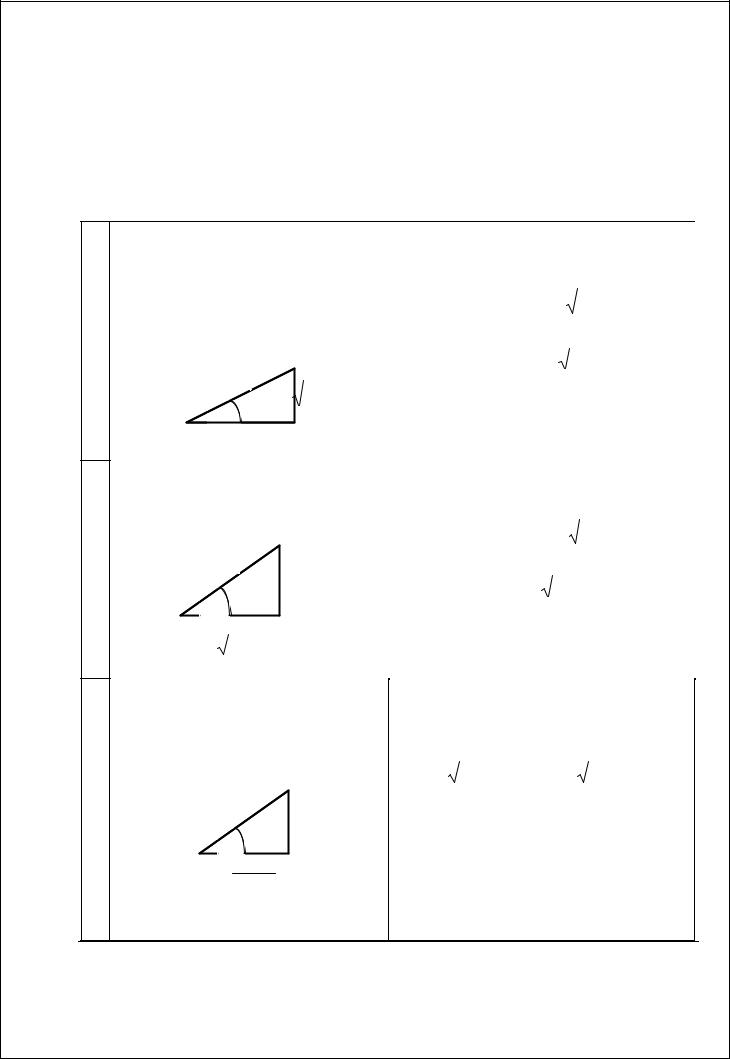
3.
Если |
|
|
|
|
|
|
|
|
|
|
|
|
то подойдёт подстановка |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
R sin x;cos x R sin x;cos x |
|
|
cos x = t. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
т.е. подынтегральное выражение яв- |
Тогда (см. рис.): |
|
sin x |
1 t 2 , |
|
|
|
||||||||||||||||||||||||||||||||||||||
ляется нечётным относительно sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|||||||||||||||||||||||
x, |
|
|
|
|
|
|
|
|
|
|
|
|
x arc cost , |
dx |
|
|
|
|
|
. |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t 2 |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
После подстановки в подынтегральное |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t 2 |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
t |
|
|
|
выражение получится просто рациональ- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ная функция от t. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
R sin x; cos x R sin x;cos x , |
то подойдёт подстановка |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
т.е. подынтегральное выражение яв- |
|
|
|
sin x = t. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
ляется нечётным относительно cos x, |
Тогда (см. рис.): |
|
cos x |
|
1 t 2 , |
|
|
||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
x arc sin t , |
dx |
|
|
dt |
|
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t 2 |
|
|
|
|
|
||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
После подстановки в подынтегральное |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выражение получится рациональная |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 t 2 |
|
|
|
функция от t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то подойдёт подстановка |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg x = t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
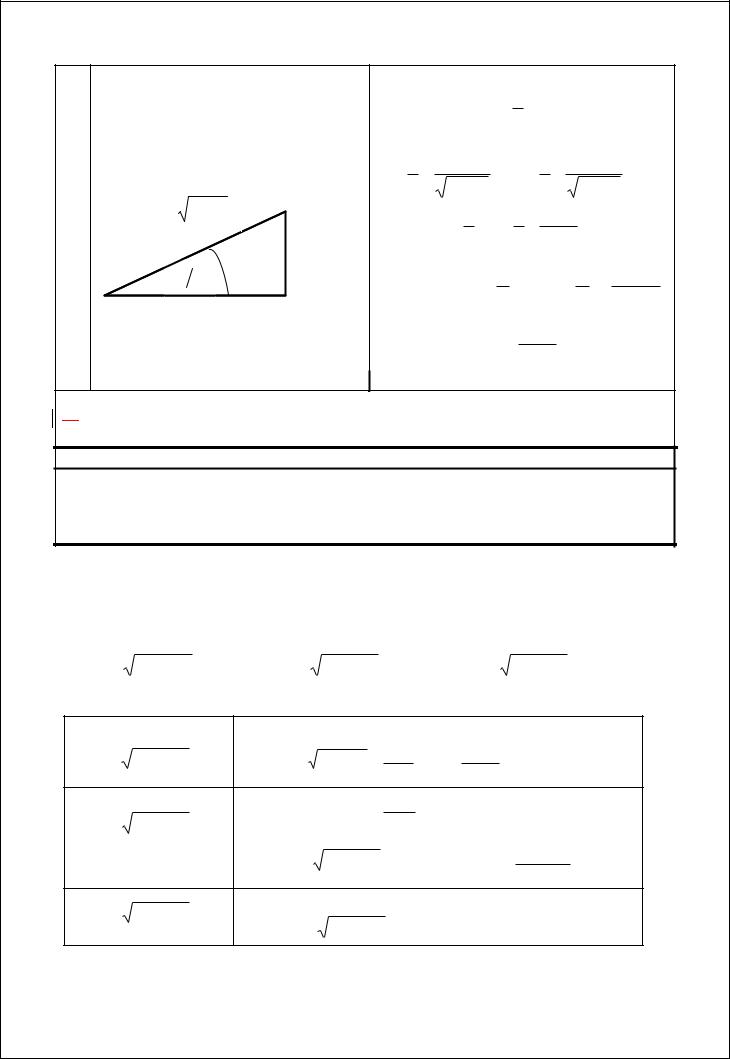
R sin x; cos x R sin x;cos x , |
Тогда (см. рис.): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
т.е. подынтегральное выражение не |
sin x |
|
t |
|
|
|
, |
|
cos x |
|
1 |
|
|
|
|
|
|
, |
|||||||||||||||||||||||||||
изменяется при одновременной заме- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
1 t |
2 |
|
|
|
1 t |
2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
не sin x на -sin x и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
cos x на -cos x, |
|
|
|
|
|
|
|
|
|
|
|
|
x arc tg t , |
dx |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
1 t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
После замены получится рациональная |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функция относительно t. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||

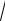 1 t 2
1 t 2
151
4. |
Во всех трех случаях, а также во всех |
|
В этом случае получаем: |
|
|
|
|
|
|||||||||||||
|
остальных случаях подойдёт универ- |
|
|
|
|
|
|
|
tg |
x |
t . |
|
|
|
|
||||||
|
сальная подстановка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
t |
|
|
, |
cos x |
|
|
1 |
, |
||
|
|
|
1 t 2 |
|
|
|
|
|
|
2 |
1 t 2 |
|
|
2 |
|
|
|
1 t 2 |
|||
|
|
|
|
|
|
|
|
sin x 2 sin x |
cos x |
|
2t |
|
, |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
t |
|
|
|
|
|
2 |
|
|
|
2 |
1 t 2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
1 t 2 |
|
|
|
x 2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
||||
|
|
|
1 |
|
|
|
|
|
cos x cos |
|
2 |
sin |
|
|
2 |
1 t 2 , |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 dt . |
|
|
|
|||
|
|
|
|
|
|
|
|
|
x 2 arc tg t , |
|
dx |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t 2 |
|
|
|
|
||
|
После подстановки в подынтегральное выражение получаем рациональную |
||||||||||||||||||||
|
функцию от переменной t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Замечание. Стоит ли во всех случаях применять универсальную подстановку? |
|||||||||||||||||||||
|
Не стоит, т.к. её применение нередко приводит к значительному усложнению |
||||||||||||||||||||
вычислений. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
14.5.7. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНОСТЕЙ С |
||||||||||||||||||||
|
|
ПОМОЩЬЮ ТРИГОНОМЕТРИЧЕСКИХ ПОДСТАНОВОК |
|
||||||||||||||||||
|
R x, |
x2 a2 dx , |
R x, |
x2 a2 dx , |
R x, |
a2 x2 dx |
|
||||||||||||||
R x, |
|
dx |
Подстановка |
x a tg t . |
|
|
|
|
|
|
|
|
|
|
|
||||||
x2 a2 |
Тогда |
x2 a 2 |
|
a , |
dx |
a2 |
dt . |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
cos t |
cos |
t |
|
|
|
|
|
|
|
||
|
R x, |
x2 a2 |
dx |
Подстановка |
x sina t . |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Тогда |
x2 a2 |
a ctg t , dx a cos t |
dt |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2 t |
|
|
|
|
||
|
R x, |
a2 x2 dx |
Подстановка |
x a sin t . |
|
|
|
|
|
|
|
|
|
|
|||||||
|
Тогда |
a |
2 |
x |
2 |
a cos t , |
dx a cos t dt |
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
152 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

14.6. ТАБЛИЦЫ ЧАСТО ВСТРЕЧАЮЩИХСЯ ИНТЕГРАЛОВ
( a,b, m, n постоянные )
14.6.1. |
|
|
|
|
|
|
|
ИНТЕГРАЛЫ ОТ РАЦИОНАЛЬНЫХ ФУНКЦИЙ, СОДЕРЖАЩИХ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ax b |
|
|
|
|||||||||
|
ax b n dx |
ax b n 1 |
|
|
C, n 1 . |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
dx |
|
1 |
|
|
ln |
|
ax b |
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
2. |
ax b |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
x dx |
|
|
|
1 |
ax b ln |
|
ax b |
|
C |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ax b |
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
3. |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
dx |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x |
|
|
|
x |
|
|
|
|
|
bx |
|
b |
ln |
|
ax b |
|
C |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
4. |
|
|
|
|
|
|
|
|
ax b |
|
|
|
2a |
|
|
|
|
|
a |
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
1 |
ln |
|
ax b |
|
|
C |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
5. |
|
|
|
x ax b |
b |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ax b |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
|
|
|
C |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
ax b |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
6. |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
bx |
|
|
b |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
x dx |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
ax |
|
b |
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
7. |
|
|
|
|
|
|
|
|
ax b |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ax b |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x2 dx |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
a |
3 |
|
|
ax 2b ln |
ax b |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
8. |
|
|
|
|
|
|
|
|
ax b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ax b |
|
||||||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
ax b |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
C |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||||
9. |
|
|
|
|
|
|
|
|
x ax b |
|
|
|
|
|
|
b ax b |
|
|
b |
|
|
|
|
|
|
|
|
x |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
153

14.6.2. ИНТЕГРАЛЫ ОТ РАЦИОНАЛЬНЫХ ФУНКЦИЙ, СОДЕРЖАЩИХ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 x2 b2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg |
|
|
|
|
|
x |
C |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
1. |
a |
2 |
x |
2 |
|
b |
2 |
|
ab |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
1 |
|
|
|
|
|
ln |
|
ax b |
|
|
C |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2. |
|
a |
2 |
x |
2 |
|
b |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ax b |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2ab |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x dx |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
ln |
|
a2 x2 b2 |
|
C |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
2 |
b |
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
3. |
|
|
|
|
|
|
a |
x |
|
|
|
|
|
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
x2 dx |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
arctg |
|
|
x |
|
C |
|
||||||||||||||||||||||||||||||||||||
4. |
|
|
|
a |
2 |
x |
2 |
b |
2 |
|
|
|
|
|
a |
2 |
|
|
a |
3 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|||||||||||||||||
5. |
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
ax b |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
x |
|
|
|
|
|
ln |
|
C |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
a |
2 |
2 |
|
2 |
|
|
2 |
|
|
|
|
|
2a |
3 |
|
ax b |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
b |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
6. |
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
ln |
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
C |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x a2 x2 b2 |
|
|
2b2 |
a2 x2 b2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
7. |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
2 |
x |
2 |
|
b |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
|
|
|
|
|
|
|
|
C |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
x a2 x2 b2 |
|
|
2b2 |
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
8. |
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg |
|
|
x |
C |
|||||||||||||||||||||||
|
x2 a2 x2 b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
b |
2 x b3 |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
9. |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
a |
|
ln |
|
ax b |
|
C |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x 2 a 2 x 2 b2 |
b2 x |
|
2b3 |
ax b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
14.6.3.ИНТЕГРАЛЫ ОТ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ,
СОДЕРЖАЩИХ 
 ax b
ax b
1.x
 ax b dx 15a2 2 3ax 2b
ax b dx 15a2 2 3ax 2b 
 ax b 3 C
ax b 3 C
2.x2 
 ax b dx 105a2 3 15a2 x2 12abx 8b2
ax b dx 105a2 3 15a2 x2 12abx 8b2 
 ax b 3 C
ax b 3 C
154
