D1_2_metodichka_metod_kinetostatiki

Федеральное агентство по образованию

Томский государственный архитектурно-строительный университет

МЕТОД КИНЕТОСТАТИКИ

(ПРИНЦИП ГЕРМАНА–ЭЙЛЕРА–ДАЛАМБЕРА)

Методические указания к самостоятельной работе

Издание второе, с изменениями

Составитель Н.А. Еньшина

Томск 2009

1

3

«Однако только Даламбер подошёл к этому принципу с более общей точки зрения и придал ему ту простоту и плодотворность, на которые только он был способен».

Лагранж

1. ВВЕДЕНИЕ

Метод кинетостатики – один из наиболее общих, эффективных и простых методов решения первой основной задачи динамики свободной и несвободной материальной точки и механической системы. В основе этого метода лежит принцип Германа–Эйлера– Даламбера.

2. ПРИНЦИП ДАЛАМБЕРА ДЛЯ МАТЕРИАЛЬНОЙ ТОЧКИ

2.1. Теория

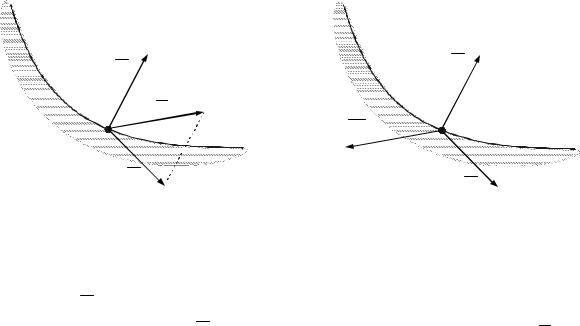
Рассмотрим несвободную материальную точку М, движущуюся по гладкой изогнутой поверхности (рис. 1, а).

б)

R R ma

F F

Рис. 1

Пусть F – равнодействующая активных сил, действующих на материальную точку М , R – реакция связи, m – масса точки, a– её ускорение. Тогда основной закон динамики для точки M запишется так [1]:

4

Векторное равенство (2.1) можно переписать следующим образом:

Введём обозначение Ф ma и назовём этот вектор силой инерции материальной точки в данное мгновение.

Сила инерции материальной точки равна произведению массы точки на её ускорение и направлена противоположно этому ус-

Полученное равенство (2.3) выражает принцип Даламбера для несвободной материальной точки: в любой момент времени для вся-

кой несвободной материальной точки геометрическая сумма равнодействующей активных сил, реакций связи и силы инерции равна нулю [1]. Для свободной материальной точки в равенстве (2.3) будет отсутствовать реакция связи R . Этот общий метод решения первой основной задачи динамики (метод кинетостатики) в 1716 году был предложен Германом и в 1737 г. обобщён Эйлером, в литературе он известен как принцип Даламбера.

В классической механике силу инерции материальной точки считаем реальной силой, противодействующей изменению скорости движущейся точки, однако приложена эта сила не к самой точке, а к телу, вызывающему ускорение данной точки.

0

Рис. 2

При криволинейном движении материальной точки её сила инерции складывается из двух составляющих – касательной (враща-

5

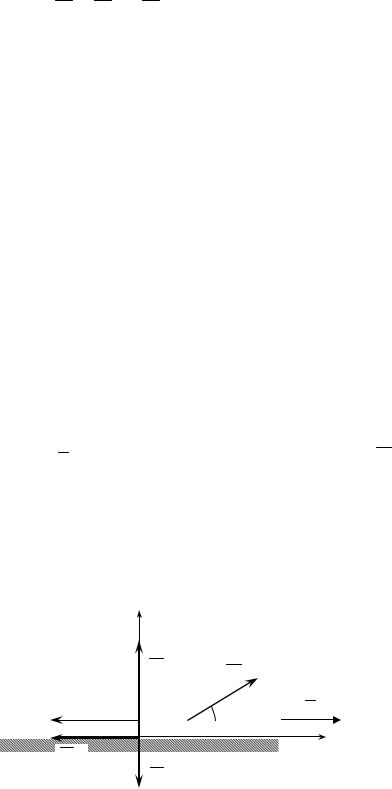
тельной) и нормальной (центробежной), – соответствующих двум составляющим ускорения – касательному и нормальному (рис. 2):

Ф Фn Ф .

Если материальная точка принадлежит вращающемуся телу и движется по окружности радиуса R, то модули касательной и нормальной сил инерции равны

Ф mR , Фn mR 2, (2.6)

где , – угловая скорость и угловое ускорение вращающегося тела.

2.2. Пример 1

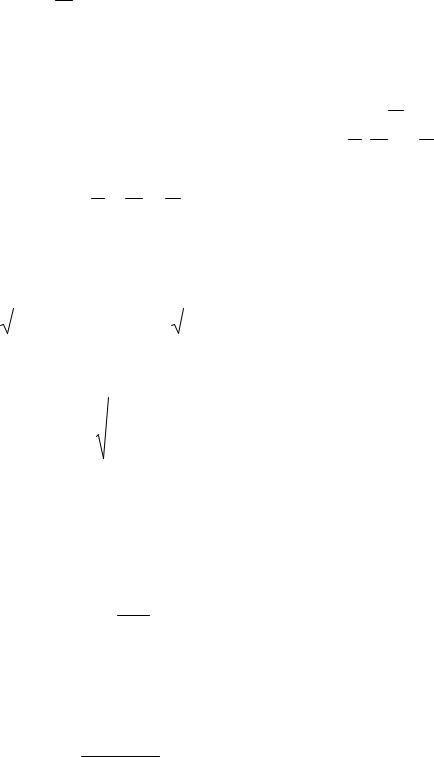
Ящик весом Р движется по горизонтальной шероховатой плоскости с ускорением a под действием некоторой силы Q , образующей с горизонтом угол ; коэффициент трения скольжения f (рис. 3).

Определить: 1) модуль силы Q; 2) значение угла и наименьшую величину силы Q, сообщающей ящику данное ускорение.

y

N Q

Fтр

x

Р

Рис. 3

6

Решение. На движущийся ящик действуют силы (рис. 3): P – сила тяжести, N – нормальная реакция плоскости, Fтр – сила трения,

Q – искомая сила. Если к этим силам присоединить ещё силу инер-

ции ящика, равную Ф Р a , то получим уравновешенную систему g

сил для данного мгновения. Согласно методу кинетостатики, составим условияравновесия для сходящихсясилв проекцияхна оси x и y:

Определим минимальное значение силы Q. Из (2.8) ясно, что силе Qmin будет соответствовать максимальное значение функцииcos f sin . Экстремальное значение функции нахо-

дится из условия d 0, откуда следует, что

максимуму функции , а следовательно, минимальному значению силы Q. После некоторых преобразований, с учётом (2.9), получим

Таким образом, найдено минимальное значение силы Q, сдвигающей ящик, направление этой силы определяется углом трения.

7

2.3. Пример 2

На криволинейных участках железнодорожного пути возвышают наружный рельс над внутренним для того, чтобы давление проходящегопоезда нарельсы былоперпендикулярнополотнудороги.

Определить величину возвышения наружного рельса над внутренним при следующих данных: радиус закругления пути400 м, скорость поезда V 10м/с, расстояние между рельсами l 1,6м.

Решение. Рассмотрим движение центра тяжести С вагона как движение материальной точки, сосредоточив его массу в этом центре тяжести (рис. 4). Тогда сила инерции, приложенная в точке С на криволинейном участке пути, направлена по радиусу закругления ОС в сторону, обратную аn , и по модулю равна

где P– вес вагона, V – его скорость, – радиус закругления полотна железной дороги. Вращательной составляющей силы инерции не будет, так как скорость поезда постоянна. Если полотно пути горизонтально (рис. 4, а), то равнодействующая сил Р и Ф не будет перпендикулярна к полотну дороги и пройдёт либо внутри полотна АВ и вызовет неодинаковое давление на рельсы (больше на наруж-

8

ный рельс), либо пройдёт вне «АВ», и вагон опрокинется. Следовательно, сила инерции Ф фактически действует на наружный рельс, стремясь вырвать крепление рельсов к шпалам. Во избежание этих опасных явлений наружный рельс возвышают над внутренним (рис. 4, б) так, чтобы давление на рельсы было перпендикулярно полотну дороги, прижимая рельсы к шпалам. Так как N – реакция рельсов, то, согласно принципу Даламбера, силы P,Ф и N вза-

Строим замкнутый силовой треугольник [4] (рис. 4, в) и из подобия силового треугольника и ABE составим пропорцию

личина при реальных скоростях по сравнению с единицей, тогда формула (2.15) упростится и будет иметь вид

g

Формула (2.16) вполне пригодна для практических целей. В условиях нашей задачи возвышение наружного рельса над внутренним h равно

h 102 1,6 0,041(м) 4,1 (см). 9,81 400

9

3. МЕТОД КИНЕТОСТАТИКИ ДЛЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ

3.1. Принцип Даламбера для механической системы

Рассмотрим несвободную механическую систему, состоящую из n материальных точек [1]. Применим к каждой i-й точке этой системы принцип Даламбера (2.3):

где Fi – равнодействующая заданных сил, приложенных к i-й точке;

Ri – равнодействующая реакций связей, наложенных на i-ю точку;

Фi – сила инерции i-й точки. Система уравнений (3.1) выражает принцип Даламбера для механической системы: если к каждой

точке движущейся механической системы условно приложить соответствующую силу инерции, то в любой момент времени действующие на эту точку активные силы, силы реакций связей и сила инерции образуют уравновешенную систему сил.

Значение принципа Даламбера состоит в том, что при его применении уравнения движения точки и системы составляются в форме уравнений статики. Метод решения динамических задач с помощью принципа Даламбера называют методом кинетостатики. Однако для решения задач применяют не сам принцип Даламбера, а следствия из него.

Сложимуравнения(3.1)длявсех n точекмеханическойсистемы:

инерции точек системы. Следовательно, (3.2) перепишется следую-

Из уравнения (3.3) следует: в любой момент времени для

всякой несвободной механической системы геометрическая сумма главных векторов заданных сил, реакций связей и сил инерции материальных точек системы равна нулю.

10