указания к курсовой инф. 2 семестр

В соответствии с учебным планом для специальностей 100100 и 210400 по курсу “Информатика” студенты выполняют курсовую работу. Курсовая работа включает в себя три раздела: составление программы на алгоритмическом языке Pascal, составление программы на алгоритмическом языке Basic и реферативное описание одной из прикладных или системных программ.

Вариант задания на курсовую работу задается преподавателем и включает в себя шесть цифр: первая – тип задачи для программы на алгоритмическом языке

Basic;

вторая – вариант задачи для программы на алгоритмическом языке Basic; третья – тип задачи для программы на алгоритмическом языке Basic; четвертая – вариант задачи для программы на алгоритмическом языке Basic; пятая – тип задачи для программы на алгоритмическом языке Basic; шестая – вариант задачи для программы на алгоритмическом языке Basic. Тип задачи расшифровывается следующим образом:

0.решение системы линейных алгебраических уравнений методом простой итерации;

1.решение системы линейных алгебраических уравнений методом ускоренной итерации;

2.решение системы линейных алгебраических уравнений методом Гаусса;

3.решение нелинейного уравнения методом половинного деления;

4.решение нелинейного уравнения методом хорд;

5.решение нелинейного уравнения методом касательных;

6.решение нелинейного уравнения методом хорд-касательных;

7.численное интегрирование по правилу прямоугольников;

8.численное интегрирование по правилу трапеций;

9.численное интегрирование по правилу Симпсона.

Варианты для каждого типа задач приведены в приложении №1.

Программу для реферативного описания студент выбирает сам, но обязательно согласует свой выбор с преподавателем.

1. Общие требования к курсовой работе

1.1.Содержание пояснительной записки.

Пояснительная записка курсовой работы должна содержать:

•титульный лист

•оглавление (содержание)

•введение

•основную часть в соответствии с заданием на курсовую работу

•заключение

•список использованных источников (литературы)

•приложения

1.2. Общие требования к основной части курсовой работы.

Разделы курсовой работы связанные с программированием на алгоритмических языках в обязательном порядке должны содержать: исходные данные, описание метода решения, алгоритм, программу на алгоритмическом

2

языке высокого уровня, результаты расчетов и проверку полученных результатов. Алгоритмы должны быть выполнены использованием любого графического редактора и соответствовать ГОСТ (Прил. 2). Проверка результатов работы программы должна быть произведена с использованием математического пакета

MathCAD.

1.3. Общие требования к оформлению текста.

Текст курсовой работы представляется на белой бумаге формата А4 (210х297мм). Титульный лист должен быть выполнен в текстовом редакторе MS Word, его вид показан в приложении 3. Перенос слов на титульном листе не разрешается, точки в конце названий курсовой работы, кафедры и специальности не ставятся. В соответствии с формой титульного листа в соответствующих местах должны быть проставлены подписи и даты.

Все материалы в пояснительной записке помещаются только на одной стороне листа с соблюдением следующих размеров полей: левое 25-30 мм, правое не менее 10 мм, верхнее и нижнее поля не менее 20 мм.

Текст пояснительной записки может быть написан от руки (за исключением текста программ и результатов расчетов) или отпечатан. В первом случае текст пишется аккуратно темными чернилами или пастой (черного, темно-фиолетового, темно-синего цвета) с расстоянием между строчками 8-10 мм (20-25 строк на страницу). Весь текст должен быть написан чернилами (пастой) одного цвета и оттенка. Во втором случае должны использоваться стандартные легко читаемые шрифты, печать выполняется через полтора или два интервала (рекомендуется шрифт Times New Roman размер 12пт интервал 1,5). Применение других цветов (кроме указанных) не разрешается.

Обнаруженные ошибки в текстовых документах устраняются с помощью специальных корректирующих средств (типа "Штрих", "Редактор" и т.д.). Вписывать отдельные слова, символы или формулы в напечатанный текст необходимо чернилами (пастой) соответствующего цвета и оттенка, при этом плотность вписанного текста должна приближаться к плотности основного. Необходимо, чтобы число исправлений на странице было минимальным. При наличии на странице более 4-5 исправлений она должна быть переделана.

Текст пояснительной записки делится на разделы, подразделы, пункты. Заголовки разделов пишутся на отдельной строке прописными буквами ("СОДЕРЖАНИЕ", ВВЕДЕНИЕ" и т.д.). Каждый раздел должен начинаться с новой страницы. Заголовок раздела отделяется от текста дополнительным межстрочным интервалом. Перенос слов в заголовке разделов, не допускается, точка в конце заголовка не ставится. Заголовки подразделов пишутся на отдельной строке. Названия пунктов пишутся на одной строке с основным текстом. Не допускается размещать заголовки подразделов и названия пунктов на одной странице, а относящийся к ним текст на следующей. Допускается выделять заголовки подразделов и названия пунктов другим шрифтом того же размера или подчеркиванием (только названия пунктов).

1.4.Нумерация.

Составные части пояснительной записки нумеруются следующим образом:

3

•разделы - в пределах всей пояснительной записки арабскими цифрами и точкой (например "3.ЧИСЛЕННОЕ ИТЕГРИРОВАНИЕ..")

•подразделы - в пределах раздела арабскими цифрами с точкой, указывается также номер раздела, к которому он относится (например "3.2.Алгоритм...");

•пункты - в пределах подраздела арабскими цифрами с точкой, указываются также номера подраздела и раздела, к которым он относится (например

"3.3.2.Попрограмма...").

Впояснительной записке осуществляется сквозная нумерация страниц арабскими цифрами. Номер страницы проставляют в правом верхнем углу. Титульный лист включают в общую нумерацию. Лист "Содержание" является первым нумерованным листом.

Иллюстрации (рисунки, блок-схемы и т.д.) нумеруются в пределах каждого раздела арабскими цифрами, указывается также номер раздела, к которому иллюстрация относится (например "Рис.3.1", "Таблица 6.4"). Обозначение "Таблица..." ставится над соответствующим заголовком в правом верхнем углу. Все остальные иллюстрации обозначаются словом "Рис...", которое располагается под ними перед соответствующим названием.

Формулы нумеруются а пределах каждого раздела арабскими цифрами, также в нумерации указывается номер раздела, к которому данная формула относится. Номер указывается с правой стороны листа на уровне формулы в круглых скобках, например: (3.1) (означает первая формула из третьего раздела).

Приложения нумеруются (если их несколько) последовательно арабскими цифрами. Страницы в приложении нумеруются в соответствии со сквозной нумерацией, принятой в пояснительной записке и оговоренными выше правилами. В нумерации разделов, формул и иллюстраций ставится буква "П" (например "Рис.П.1.1." - первый рисунок первого приложения).

1.5.Иллюстрации.

Рисунки, блок-схемы, графики могут располагаться либо на странице непосредственно в тексте, либо на отдельных листах, в том числе и по несколько иллюстраций на одном листе. Каждая иллюстрация должна иметь наименование, а при необходимости и поясняющие данные, которые располагаются под ней.

2.Методические указания для различных типов задач

2.1.Решение систем линейных алгебраических уравнений.

2.1.1 Общие сведения.

Системы алгебраических уравнений (СЛАУ) имеют вид:

или, при записи в матричной форме:

4

A x =b ,x1

где x = x2 – вектор искомых неизвестных,

xn

В практике используют два типа методов численного решения СЛАУ – прямые и косвенные. При использовании прямых методов СЛАУ приводится к одной из специальных форм (диагональной, треугольной) позволяющих точно получить искомое решение (если таковое существует). Наиболее распространенным прямым методом решения СЛАУ является метод Гаусса. Итерационные методы служат для поиска приближенного решения СЛАУ с заданной точностью. Следует отметить, что итерационный процесс не всегда сходится к решению системы, а только тогда, когда последовательность получаемых при расчетах приближений стремиться к точному решению.

2.1.2 Метод простой итерации.

При решении СЛАУ методом простой итерации ее преобразуют к виду, когда в левой части находится только одна из искомых переменных:

Задав некоторые исходные приближения xi, i=1,2,…,n, подставляют их в правую часть выражений и вычисляют новые значения x. Процесс повторяют до тех пор, пока максимальная из невязок, определяемых по выражению:

n

ri =bi − ∑aij x j ,i =1,2,…, n

j =1

5

не станет меньше заданной точности ε. Если максимальная невязка при k-ой итерации окажется больше максимальной невязки при k-1-ой итерации, то процесс аварийно завершают, т.к. итерационный процесс расходится.

Для минимизации количества итераций новые значения x можно вычислять с использованием значением невязок на предыдущей итерации:

Невязки, в этом случае определяют по выражению: ri(k ) = −bi +∑n aij x(jk −1) , i =1,2,...,n .

j=1

2.1.3Метод ускоренной итерации.

Его отличие от метода простой итерации состоит в том, что при вычислении нового приближения переменной x2(k ) используется значение x1(k ) , а не значение x1(k −1) . Аналогично для вычисления всех последующих значений x, по возможности,

используют значения, полученные на данной итерации. Таким образом, алгоритм решения СЛАУ методом ускоренной итерации аналогичен алгоритму метода простой итерации, за исключением невязок, которые определяются по выражению:

2.1.3 Метод Гаусса.

Данный метод основан на упорядоченном исключении неизвестных из СЛАУ и приводит к решению за заранее известное количество операций (если матрица не является вырожденной).

Решение СЛАУ выполняется в два этапа. На первом этапе приводят систему к треугольной форме, пересчитывая значения матрицы A и вектора b. Данный этап называют прямым ходом. На втором этапе упрощенную систему решают методом подстановки. Этот этап называют обратным ходом.

Рассмотрим более подробно решение системы из n уравнений:

Прямой ход.

На первом шаге выразим из первого уравнения переменную x1:

6

Подставляя данное выражение в исходную СЛАУ, исключим из второго и последующих уравнений x1 и получим систему следующего вида:

где верхний индекс указывает номер шага прямого хода. На втором шаге из второго уравнения полученной системы выразим x2 и повторим преобразования описанные выше. Получим новую матрицу.

Аналогично выполнив n-1 шаг, получим преобразованную треугольную систему:

В приведенных выше выражениях через индекс k обозначен шаг преобразования матрицы. Необходимо отметить, что при равенстве нулю элемента akk следует найти элемент aik ≠ 0, при i>k и поменять местами i-ую и k-ую строки. Если такой элемент отсутствует, то вычисления аварийно прекращают и говорят, что матрица выраждена. Для повышения точности расчетов следует производить перестановку уравнений таким образом, чтобы главный элемент akk, на каждом шаге был максимальным.

7

Обратный ход.

Из последнего уравнения преобразованной системы находим

xn = bn

ann

и далее по выражению

bi − ∑n aij x j

где i=n-1, n-2,…,1; находим вектор искомых неизвестных.

2.2. Решение нелинейных уравнений.

2.2.1 Общие сведения.

Уравнение типа F(x)=0 или x=f(x) называется нелинейным. Решить уравнение это значит найти такое x, при котором уравнение превращается в тождество. В общем случае уравнение может иметь 0; 1; 2;...∞ корней. Рассмотренные ниже численные методы решения нелинейных уравнений позволяют находить один корень на заданном интервале [a,b]. При этом на интервале должен существовать только один корень.

Решение уравнения складывается из двух этапов:

1.отделения корня, т.е. грубой оценки значения корня, которое используется в качестве начального приближения при его последующем уточнении;

2.уточнения корня, т.е. доведения его численного значения до заданной степени точности.

Для отделения корня (определения начального приближения) следует пользоваться графическим методом. Уточнение корня может быть произведено одним из следующих методов.

2.2.2 Метод половинного деления.

При решении нелинейного уравнения методом половинного деления задаются интервал [a,b], на котором существует только одно решение, и желаемая точность ε. Затем определяется середина интервала с=(а+b)/2 и проверяется условие F(a)·F(c)<0. Если указанное условие выполняется, то правую границу интервала b переносим в среднюю точку с (b=c). Если условие не выполняется, то в среднюю точку переносим левую границу(a=c). Деление отрезка пополам продолжается пока |b-a|>ε.

2.2.3 Метод хорд.

При решении нелинейного уравнения методом хорд задаются интервал [a,b], на котором существует только одно решение, и точность ε. Затем через две точки с координатами (a,F(a)) и (b,F(b)) проводим отрезок прямой линии (хорду) и определяем точку пересечения этой линии с осью абсцисс (точка c). Если при этом F(a)·F(c)<0, то правую границу интервала переносим в точку с (b=c). Если

8

указанное условие не выполняется, то в точку c переносится левая граница интервала (а=с). Поиск решения прекращается при достижении заданной точности |F(c)|< ε. Для определения точки пересечения хорды с осью абсцисс воспользуемся следующей формулой

2.2.4 Метод касательных.

При решении нелинейного уравнения методом касательных задаются начальное значение аргумента x0 и точность ε. Затем в точке(x0,F(x0)) проводим касательную к графику F(x) и определяем точку пересечения касательной с осью абсцисс x1. В точке (x1,F(x1)) снова строим касательную, находим следующее приближение искомого решения x2 и т.д. Указанную процедуру повторяем пока |F(xi)| > ε. Для определения точки пересечения (i+1) касательной с осью абсцисс воспользуемся следующей формулой

xi+1 = xi − F′(xi ) F (xi )

Условие сходимости метода касательных F(x0)·F''(x0)>0.

2.2.5 Метод хорд-касательных.

Если в методе касательных производную функции F'(xi) заменить отношением конечных приращений, то получаем расчетную формулу для метода хорд-касательных

Порядок выполнения вычислений в данном методе аналогичен рассмотренному ранее.

2.3. Численное интегрирование.

2.3.1 Общие сведения.

Определенным интегралом функции f(x), взятом в интервале от a до b,

9

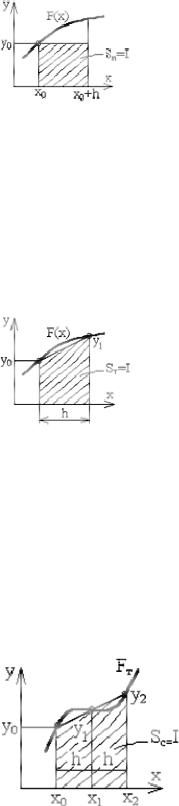
где Ii - элемент интегральной суммы. Заменяя подынтегральную функцию на каждом шаге отрезками линий нулевого, первого и второго порядков, получаем приближенные формулы для вычисления интеграла методами прямоугольников, трапеций и Симпсона соответственно.

2.3.2 Правило прямоугольников.

Заменяем график функции F(x) горизонтальной линией (линии нулевого порядка) и вычисляем значение элемента интегральной суммы как площадь прямоугольника

x0 +h

I = ∫ F (x)dx ≈ y0 h ,

x0

где h - шаг интегрирования, у0 - значение функции в точке х=х0 у(х0)=у0

2.3.3 Правило трапеций.

Заменяем график функции F(x) прямой, проходящей через две точки (х0,у0) и (х0+h,у1), и вычисляем значение элемента интегральной суммы как площадь трапеции

2.3.4 Правило Симпсона.

10