§2. Кинематика

2.1. Кинематика материальной точки

2.1.1. Способы описания движения материальной точки

Существуют различные способы описания движения материальной точки. Рассмотрим так называемые векторный и координатный способы.

Рис. 2.1

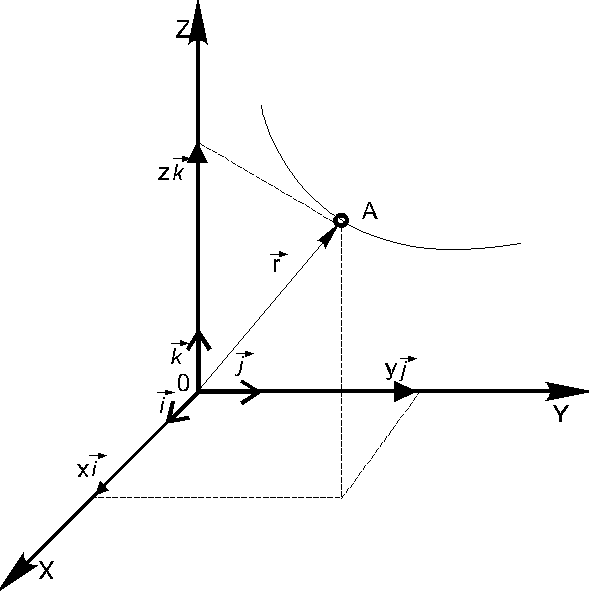
В векторном способе положение материальной точки А задают радиус-вектором , проведенным из начала выбранной системы координат (рис. 2.1) в точку А. При движении точки А ее радиус-вектор изменяется в общем случае как по модулю, так и по направлению, т.е. радиус-вектор зависит от времени t. Математически это записывается в виде векторного уравнения

. (2.1)

Вектор можно разложить по осям координат X, Y и Z с помощью соответствующих ортов (единичных векторов) ,и:

, (2.2)

где - составляющие вектора по осям системы координат;x, у и z - координаты точки А и одновременно проекции вектора на соответствующие оси.

В координатном способе описания движения материальной точки, основанном также на использовании какой-либо системы координат, составляются временные зависимости (уравнения) для координат данной точки. Например, для точки А в выше приведенном случае эти уравнения будут иметь вид:

, ,.(2.3)

Зная зависимость координат от времени - закон движения материальной точки, можно найти ее положение в любой момент времени.

Уравнения вида (2.1) и (2.3) называют кинематическими уравнениями движения материальной точки.

2.1.2. Кинематические характеристики материальной точки

К кинематическим характеристикам относятся траектория, длина пути, перемещение, скорость и ускорение.

Траекторией называется линия, описываемая в пространстве точкой в процессе движения.

Кинематические уравнения движения материальной точки задают уравнение ее траектории в параметрической форме (параметр - время t). В зависимости от формы траектории различают прямолинейное и криволинейное движение точки. Движение точки называется плоским, если ее траектория целиком лежит в одной плоскости.

Для описания криволинейных траекторий используются понятия радиуса кривизны и центра кривизны траектории.

Рис. 2.2

Радиус кривизны траектории в точке М представляет собой радиус окружности (рис. 2.2), которая сливается в данном месте с бесконечно малым участком траектории. Эта окружность проходит через три точки М₁, М и М₂, когда точки М₁ и М₂ неограниченно приближаются к точке М.

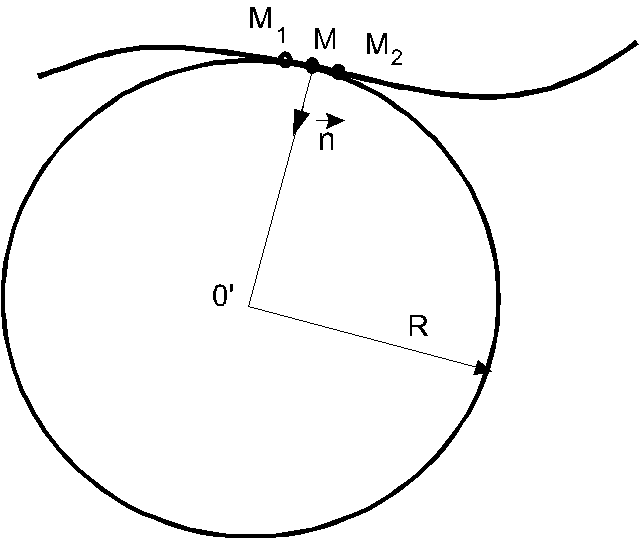
Центр О' такой окружности называется центром кривизны траектории в точке М. Единичный вектор , направленныйиз точкиМ к центру кривизны, называется главной нормалью к траектории в точке М.

Расстояние, отсчитанное вдоль траектории, называется длиной пройденного телом пути за рассматриваемый промежуток времени.

Рис. 2.3

Единица измерения длины пути в СИ - метр (м).

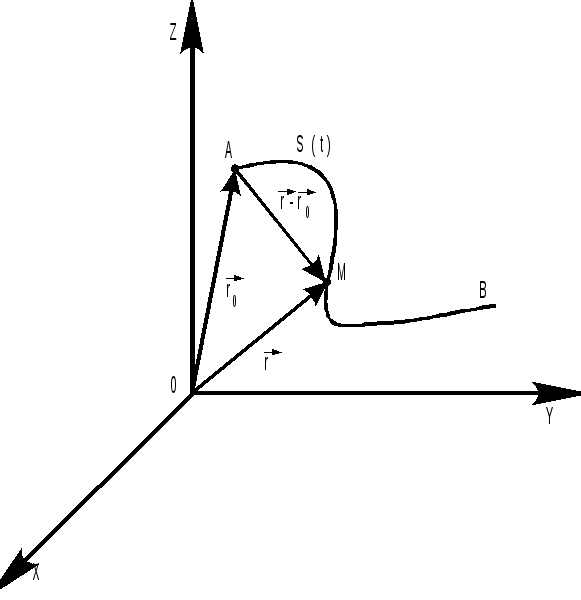
Момент времени t=t₀ , ранее которого движение точки не рассматривается, называется начальным моментом времени (часто выбирают t₀=0), а положение точки в этот момент (точка А на рис. 2.3) - начальным положением. Длина пути S является скалярной функцией времени: S=S(t), и не может быть отрицательной величиной. Если точка движется по дуге траектории AB все время в одном направлении и в момент времени t находится в точке М, то S(t)= AM. Если же точка движется по траектории более сложным образом, например перемещается из А в B, а затем, двигаясь в обратном направлении, возвращается в точку М, то S(t)= AB+BM (см. рис. 2.3).

Перемещением точки за время от t₁ до t₂ называется вектор, проведенный из положения точки в момент времени t₁ , в положение в момент t₂.

На рис. 2.3 показан вектор перемещения материальной точки за промежуток времени от t₀ до t₁, равный

. (2.4)

Для характеристики движения тел в механике вводится понятие скорости. Математическое содержание понятия скорости определим через среднюю скорость. Пусть материальная точка движется по криволинейной траектории MN (рис. 2.4) так, что в момент времени t она находится в точке М, а в момент времени (t+t) - в точке N.

Радиус-векторы точек М и N соответственно равны и, а длина дуги MN равна S.

Средней скоростью движущейся материальной точки в интервале времени от t до (t+t) называется вектор , равный отношению вектора перемещения точки к этому промежутку времени t:

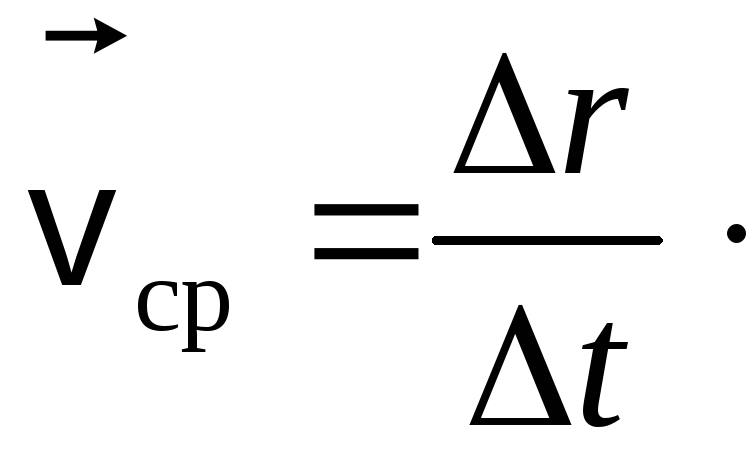
(2.5)

Вектор направлен так же, как , то есть вдоль хорды, стягивающей соответствующий участок траектории точки (см. рис. 2.4).

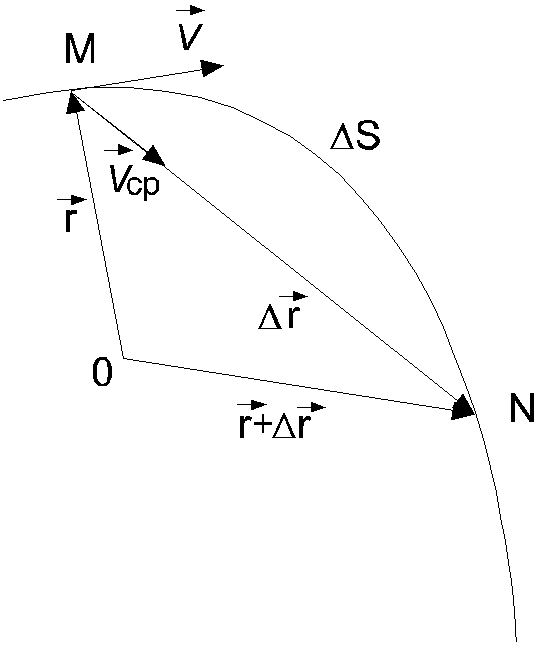
Если в выражении (2.5) перейти к пределу, устремляя t к нулю, то получим выражение для скорости (или мгновенной скорости) материальной точки в момент времени t прохождения ей через точку М

Рис. 2.4

траектории:

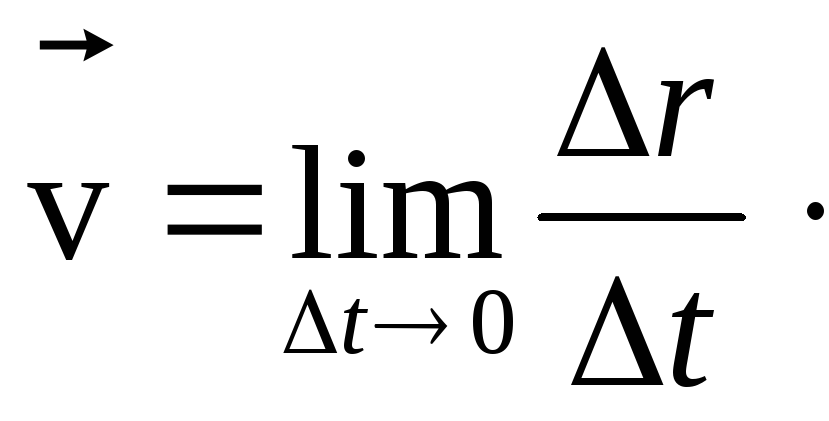
Полученное выражение может быть записано с помощью понятия производной.

Производной функции y = f(x) по независимой переменной х называется предел отношения приращения функции к соответствующему приращению независимой переменной, при условии, что приращение х стремится к нулю:

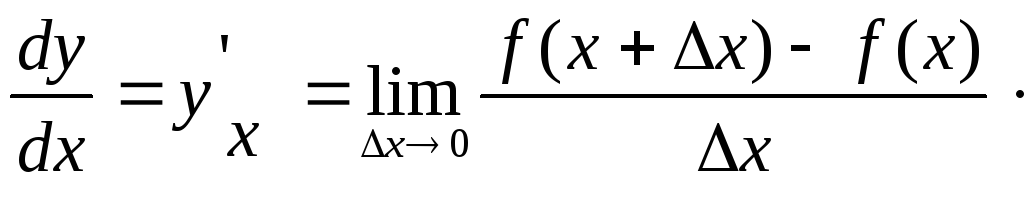
Таким образом, мгновенная скорость определяется выражением:

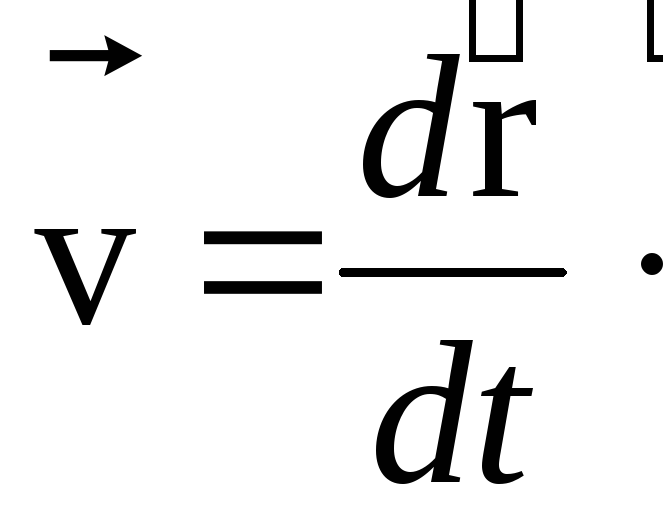(2.6)

Из этого выражения следует, что мгновенной скоростью материальной точки называется векторная величина, равная первой производной по времени от радиус-вектора рассматриваемой точки.

Единица измерения скорости в СИ - метр, деленный на секунду (м/с).

В процессе уменьшения величины t точка N приближается к точке М, и хорда MN в пределе совпадает по направлению с касательной к траектории в точке M. Таким образом, и вектор , и вектор мгновенной скоростидвижущейся точки направлены по касательной к траектории в сторону движения. Найдем модуль, т.е. численное значение, скорости:

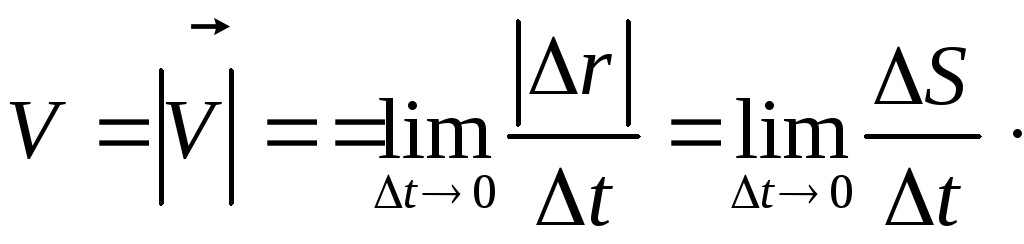(2.7)

Из математики известно, что предел отношения длины S дуги к длине, стягивающей ее хорды, равен единице при S0. Поэтому модуль малого (элементарного) приращения радиус-вектораравен длинеds, соответствующей дуги траектории:

^. (2.8)

Из этого равенства и выражения (2.7) следует, что

^. (2.9)

Скорость материальной точки можно разложить на три составляющие, направленные вдоль осей координат:

, (2.10)

где - проекции скорости на оси координат.

Подставив в (2.6) выражение (2.2) и выполнив дифференцирование, получим

^. (2.11)

Из сопоставления выражений (2.10) и (2.11) следует, что

, и^, (2.12)

то есть проекции скорости материальной точки на оси прямоугольной декартовой системы координат равны первым производным по времени от соответствующих координат точки. В этом случае модуль скорости определяется из выражения

^. (2.13)

Е

Рис 2.5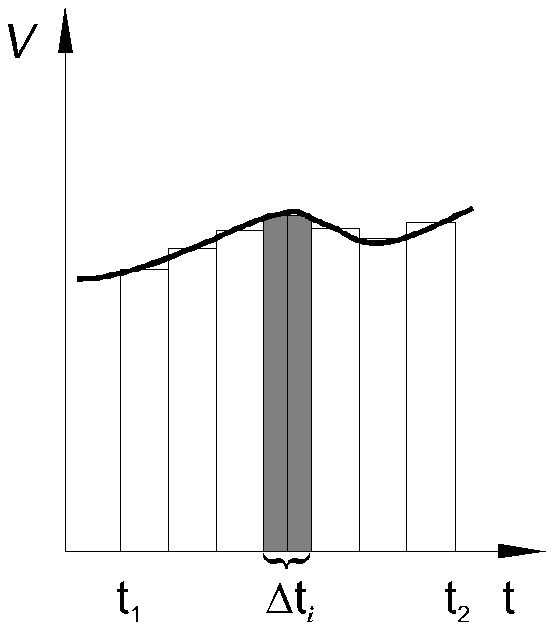

сли известен модуль скорости точки в каждый момент времени, то можно вычислить путь, пройденный ею за время от t₁ до t₂ (рис. 2.5). Для этого разобьем время t₂ - t₁ на n малых промежутков: t₁, t₂…t_n. Весь путь S можно представить как сумму путей:

S=S₁+S₂+…+S_n=, (2.14)

где i - любое из чисел от 1 до n, а символ использован для сокращенной записи n слагаемых одинакового вида. Каждое из слагаемыхS_i может быть представлено приближенным равенством, которое получается из выражения (2.7) при малых t:

S_iV_i(t) t_i, (2.15)

где V_i(t) - одно из значений скорости за время t_i.

Подставим равенство (2.15) в формулу (2.14), тогда получим

(2.16)

Равенство (2.16) выполняется тем точнее, чем меньше промежуток времени t_i. В пределе при стремлении всех t_i к нулю сумма в (2.16) станет точно равна S:

^. (2.17)

Правая часть выражения (2.17) в математике называется определенным интегралом от функции V(t)в пределах от t₁ до t₂ и записывается символически:

^.

Следовательно, путь, пройденный точкой за время от t₁ до t₂, равен:

^. (2.18)

Интеграл имеет простой геометрический смысл. На рис. 2.5 приведен график функции V=V(t). Произведение V_i(t)^.t_i равно площади заштрихованной i-ой полоски. Сумма таких произведений будет равна площади ступенчатой фигуры. При стремлении t_i к нулю в пределе площадь этой фигуры станет равна площади, ограниченной графиком V(t), осью t и прямыми t=t₁ и t=t₂.

В зависимости от того, как изменяется скорость, движение называют равномерным или ускоренным (замедленным), прямолинейным или криволинейным.

Если в процессе движения точки модуль ее скорости не изменяется (направление вектора скорости может изменяться), то есть , то такое движение называетсяравномерным. При этом, как следует из (2.18), длина пути, пройденного точкой, линейно зависит от времени:

^. (2.19)

Если модуль скорости точки увеличивается с течением времени (), то движение называется ускоренным, если же он убывает с течением времени (), то движение называется замедленным.

В случае, если направление скорости точки в процессе движения не изменяется (модуль скорости может оставаться постоянным или изменяться), то такое движение называется прямолинейным. Это означает, что траектория при таком движении представляет собой прямую линию или ее отрезок. Если же направление скорости со временем изменяется, то точка обязательно описывает криволинейную траекторию.

Рис. 2.6

Очень часто движение тел характеризуется переменным по модулю и направлению вектором скорости. Для характеристики изменения скорости вводится понятие ускорения. Как и в предыдущем случае, математическое содержание понятия ускорения введем через понятие среднего ускорения.

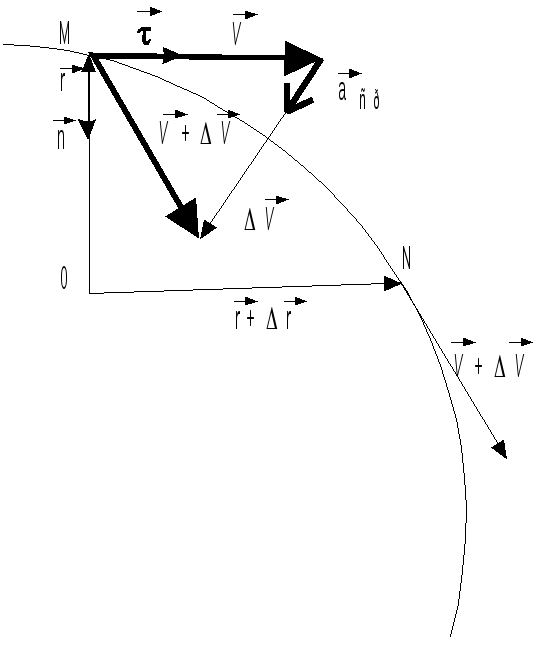
Пусть за время t материальная точка перешла из положения M в положение N (рис. 2.6), и ее скорость изменилась на. Перенесем вектор () из точкиN в точку М.

Средним ускорением материальной точки в интервале времени от t до t+t называется вектор , равный отношению приращения вектора скорости точки за этот промежуток времени к его продолжительности t:

^. (2.20)

Вектор совпадает по направлению с вектором изменения скорости .

При переходе в (2.20) к пределу при стремлении t к нулю получается выражение для ускорения (или мгновенного ускорения) материальной точки в момент времениt прохождения ее через точку M траектории:

(2.21)

или с учетом формулы (2.6)

^. (2.22)

Из этого выражения следует, что ускорением материальной точки называется векторная величина, характеризующая изменение скорости точки (по модулю и направлению) и равная первой производной по времени от скорости или, что то же самое, второй производной по времени от радиус-вектора этой точки.

Единица ускорения в СИ – метр, деленный на секунду в квадрате (м/с²).

Вектор ускорения материальной точки можно разложить на три составляющие, направленные вдоль осей координат:

, (2.18)

где - проекции ускорения на оси координат.

Подставив в (2.16) выражения (2.10) и (2.11) и выполнив дифференцирование, получим

^. (2.19)

Из сопоставления выражений (2.18) и (2.19) следует, что

, и, (2.20)

то есть проекции ускорения материальной точки на оси прямоугольной декартовой системы координат равны первым производным по времени от соответствующих проекций скорости этой точки или вторым производным по времени от соответствующих координат точки.