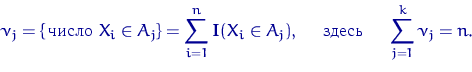Федеральное агентство связи

Федеральное государственное образовательное бюджетное учреждение

высшего профессионального образования

«Сибирский государственный университет телекоммуникаций и информатики»

Кафедра математического

моделирования бизнес-процессов

Курсовая работа по математической статистике

Выполнила: студентка

II курса, ИВТ, гр. ИБ-19

Баранова А. И.

Проверила: Чернова Н. И.

Новосибирск, 2012

1. Теоретическая часть

1.1 Выборка

Генеральная совокупность – это случайная величина X(ω), заданная на пространстве элементарных событий Ω с выделенным в нём классом подмножеств событий, для которых указаны их вероятности.

Выборочной совокупностью (выборкой) называется совокупность объектов, отобранных случайным образом из генеральной совокупности.

Выборка – это набор n независимых в совокупности и одинаково распределённых случайных величин (X₁, X₂, ..., X_n), где X_i соответствует i-му по счёту эксперименту, а число n называется объёмом выборки.

Совокупность чисел (x₁,x₂, …, x_n), полученных в результате n-кратного повторения опыта по измерению генеральной совокупности X, называется реализацией случайной выборки или просто выборкой объёма n.

1.2 Эмпирическая функция распределения

Эмпирической функцией распределения, построенной по выборке объема , называется случайная функция , при каждом равная

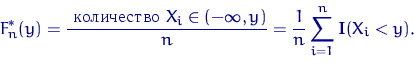
При любом значение , равное истинной вероятности случайной величине быть меньше , оценивается долей элементов выборки, меньших .

Эмпирическая функция распределения имеет скачки в точках выборки, величина скачка в точке равна , где — количество элементов выборки, совпадающих с .

1.3 Гистограмма

Гистограмма строится по группированным данным. Предполагаемую область значений случайной величины (или область выборочных данных) делят независимо от выборки на некоторое количество интервалов (не обязательно одинаковых). Пусть , , — интервалы на прямой, называемые интервалами группировки. Обозначим для через число элементов выборки, попавших в интервал :

На каждом из интервалов строят прямоугольник, площадь которого пропорциональна . Общая площадь всех прямоугольников должна равняться единице. Пусть — длина интервала . Высота прямоугольника над равна

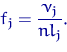
Полученная фигура называется гистограммой.

1.4 Выборочные моменты

Выборочным средним называется среднее арифметическое всех значений выборки:

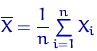
Выборочный-й момент:

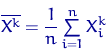
Выборочной дисперсией называется среднее арифметическое квадратов отклонений значений выборки от выборочного среднего:

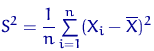
Несмещённая выборочная дисперсия:

1.5 Доверительные интервалы

Пусть . Интервал называется доверительным интервалом для параметра уровня доверия , если для любого

Доверительные интервалы для параметров нормального распределения:

• Для при неизвестном

),

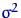
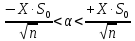где x такое, что .

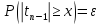• Для 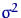при известном

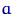
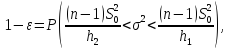
где h₁: P(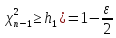 и h₂: P(.

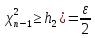1.6 Критерий хи-квадрат Пирсона

Критерий основывается на группированных данных. Область значений предполагаемого распределения  делят на некоторое число интервалов. После чего строят функцию отклонения  по разностям теоретических вероятностей попадания в интервалы группировки и эмпирических частот.

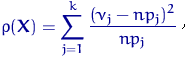
где - число элементов выборки в j-м интервале, p_j - теоретические вероятности попадания в j-й интервал случайной величины с распределением .

Пусть задан набор вероятностей такой, что .

Критерий предназначен для проверки сложной гипотезы

против сложной альтернативы , т.е.

Теорема Пирсона:

Если верна гипотеза , то при фиксированном и при

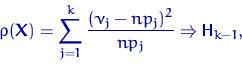
где есть -распределение с степенью свободы.

Пусть случайная величина имеет распределение . По таблице распределения найдем равное квантили уровня этого распределения. Тогда и критерий согласия выглядит как все критерии согласия:

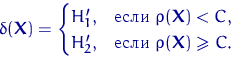
1.7 Критерий Фишера

Есть две независимые выборки из нормальных распределений: из и из , средние которых, вообще говоря, неизвестны. Критерий Фишера предназначен для проверки гипотезы .

Обозначим через и несмещенные выборочные дисперсии:

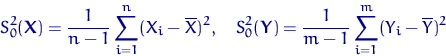
и зададим функцию отклонения как их отношение

Если гипотеза верна, то случайная величина имеет распределение Фишера с степенями свободы.

Возьмем квантили и распределения Фишера . Критерием Фишера называют критерий:

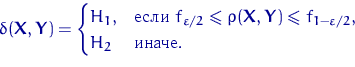
1.8 Критерий Стьюдента

Есть две независимые выборки: из и из , причем дисперсия одинакова для обоих распределений, но неизвестна. Проверяется сложная гипотеза.

Введём функцию

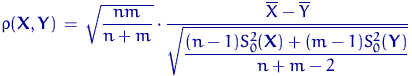
Если верна, то величина имеет распределение Стьюдента с степенями свободы.

Нужно по 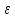найти - квантиль распределения . Для такого величина из распределения удовлетворяет равенству

Таким образом, Критерий Стьюдента:

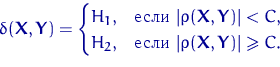
Выборка №3

-3.002	-1.155	-3.484	-2.017	-2.012	-1.783	-3.059	-3.488	-1.431	-3.104
-1.459	-2.284	-2.156	-2.238	-2.238	-1.616	-1.722	-2.053	-1.048	-1.070
-2.557	-1.787	-2.774	-3.401	-1.144	-2.926	-2.371	-1.907	-0.576	-1.832
-2.399	-2.331	-2.602	-2.687	-2.512	-1.480	-2.773	-1.319	-2.473	-3.196
-1.418	-2.454	-2.289	-1.939	-1.780	-2.792	-1.533	-3.945	-1.946	-2.025

Список литературы

1. Коршунов Д.А., Чернова Н.И. Сборник задач и упражнений по математической статистике. Учебное пособие. – 2-е изд., испр. - Новосибирск: Изд-во Института математики, 2004. – 128 с.

2. Письменный Д. Т. Конспект лекций по теории вероятностей и математической статистике и случайным процессам. - М.: Айрис-пресс, 2004. - 256 с.