4. Поиск минимального пути от источника к стоку сети.

4.1 Поиск минимального пути от источника к стоку сети в MatCad.

Если вес дуги трактовать, как стоимость перевозки по этой дуге, то можно поставить задачу по нахождению пути, который обеспечит минимальную стоимость перевозки по сети.

Вес, данный каждой дуге, будем трактовать, как длину дуги.

Будем считать, что весь поток, входящий в узел, равен потоку, исходящий из узла. Получим ограничение на отсутствие задержки потока в узлах:

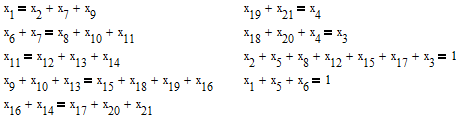
Длину можно вычислить как:

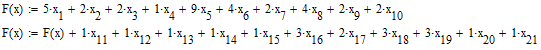
Получим задачу линейной оптимизации:

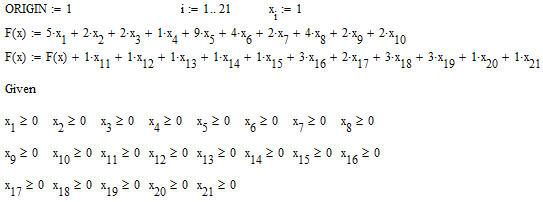
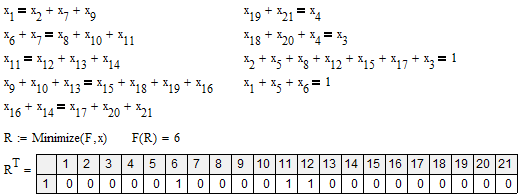
Вектор решения R определяет, какие дуги задействованы в минимальном пути. 1 – задействована, 0 – не задействована. При этом величина минимального пути = 6.

На приведенной ниже графической интерпретации видно, что найденный минимальный путь является единственным равным длине 6:

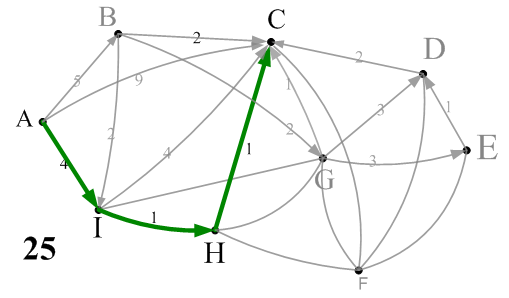
4.2 Поиск минимального пути от источника

к стоку сети в Excel

Подготовка бланка решения:

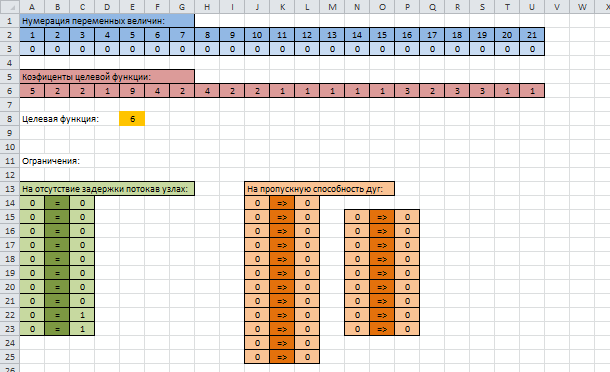
Подготовка бланка решения (в режиме формул):

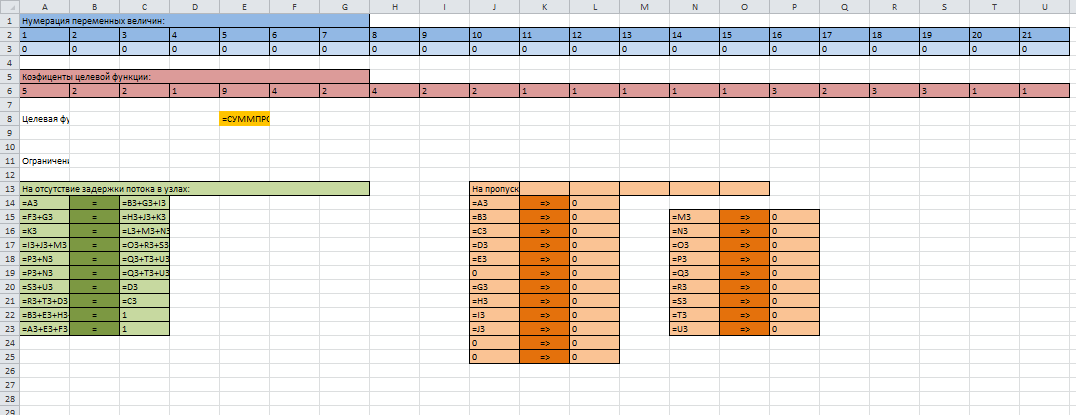
Заполнение параметров поиска решений:

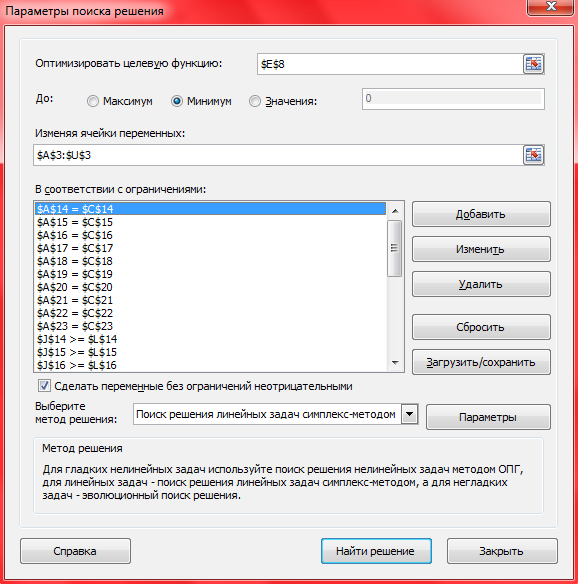
Устанавливаем параметры:

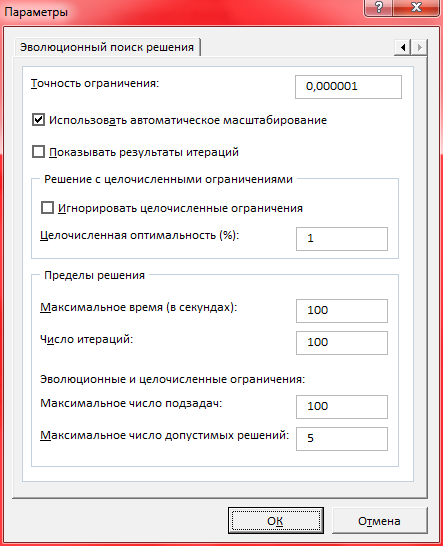
Нажимаем OK→ Выполнить → Сохранить найденное решение →OK

Результат:

5. Решение задачи о «Назначениях рабочих».

5.1 Решение задачи о

«Назначениях рабочих» в MathCad.

Так как условия задачи неоднозначны, имеется возможность в двух вариантах интерпретировать ответ. Воспользуемся матрицей из условий:

	Столб. 1	Столб. 2	Столб. 3	Столб. 4	Столб. 5	Столб. 6
Строк.1	3 x1	6 x2	4 x3	5 x4	4 x5	2 x6
Строк.2	1 x7	3 x8	2 x9	1 x10	3 x11	5 x12
Строк.3	5 x13	5 x14	5 x15	5 x16	1 x17	4 x18
Строк.4	4 x19	5 x20	6 x21	7 x22	1 x23	9 x24
Строк.5	2 x25	6 x26	6 x27	6 x28	1 x29	7 x30
Строк.6	5 x31	6 x32	4 x33	5 x34	1 x35	5 x36

Сумма всех элементов строки матрицы, должна быть равной1, так как сотрудников 6 и их всех примут на работу. Сумма всех элементов одного столбца матрицы тоже, должна бытьравной1, так как на одно рабочее место должен быть назначен один сотрудник.

Общее количество всех назначений можно вычислить как:

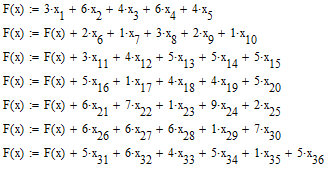
Учитываем ограничения:

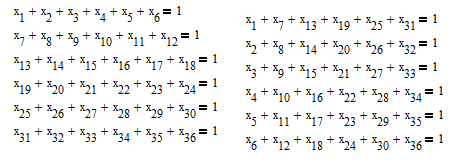
Получаем задачу оптимизации:

Для большей наглядности преобразуем транспонированный вектор в матрицу:

Матрица показывает, как будут распределены рабочие, например, вариант 1 показывает, что Раб. 1будет работать наМест. 5и т.д. При этом минимальные затраты на производство будут равны 15. Матрица не однозначна, так как дать имена строкам и столбцам можно по-разному:

Вариант 1:

	Раб. 1	Раб. 2	Раб. 3	Раб. 4	Раб. 5	Раб. 6
Мест. 1						+
Мест. 2				+
Мест. 3					+
Мест. 4		+
Мест. 5	+
Мест. 6			+

Вариант 2:

	Мест. 1	Мест. 2	Мест. 3	Мест. 4	Мест. 5	Мест. 6
Раб. 1					+
Раб. 2				+
Раб. 3						+
Раб. 4		+
Раб. 5			+
Раб. 6	+

Из обеих интерпретаций решений видно, что при разном распределении сотрудников на места, затраты на производство по-прежнему будут равны 15.