
ДМ_гл2_DO
.doc-
Треугольник Паскаля
Из второй формулы теоремы 2.4 следует удобный способ рекуррентного вычисления значений биномиальных коэффициентов, который можно представить в графической форме, известной как треугольник Паскаля.
|
В C(5,2) |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
2 |
|
1 |
|
|
|
|
2 |
|
|
|
|
|
1 |
|
3 |
|
3 |
|
1 |
|
|
|
3 |
|
|
|
|
1 |
|
4 |
|
6 |
|
4 |
|
1 |
|
|
4 |
|
|
|
1 |
|
5 |
|
10 |
|
10 |
|
5 |
|
1 |
|
5 |
|
|
… |
|
… |
|
… |
|
… |
|
… |
|
… |
|
… |
|
-
Контрольные вопросы
-
Запишите в виде многочлена (a+b)4, используя формулу бинома Ньютона.
-
Найдите значение выражения C(4,2)+C(4,0)+C(4,3)+C(4,1)+C(4,4).
-
Используя треугольник Паскаля, вычислите C(7,3). Проверьте полученное значение по формуле для числа сочетаний.
-
Найти n, если в разложении (1+x)n коэффициенты при x5 и x12 одинаковы.
-
Обобщенные перестановки и разбиения
-
Перестановки с повторениями
Пусть совокупность элементов X содержит n объектов k различных типов, причем имеется n1 неразличимых объектов типа 1, n2 неразличимых объектов типа 2, …, ni неразличимых объектов типа i. Обозначим количество различных размещений элементов множества X через P(n; n1, n2, …, nk). Тогда такие размещения называются перестановками с повторениями и их количество вычисляется по формуле
![]() (2.3)
(2.3)
-
Сколько разных слов можно образовать при перестановке букв слова «математика»? Здесь типы объектов – это различные буквы (число типов k=6), количество неразличимых объектов каждого из типов – это число повторений конкретной буквы. Если бы все буквы были различны, то таких слов = 10!. Количество перестановок, в которых меняются местами только k одинаковых букв, равно k! Очевидно, что такие перестановки не меняют полученного слова при подсчете нужно разделить 10! на k!, и выполнить это для всех повторяющихся элементов. В слове «математика» буква «м» встречается 2 раза, «а» – 3 раза, «т» – 2 раза, «е» – 1 раз, «и» – 1 раз, «к» – 1 раз. Поэтому число различных слов равно
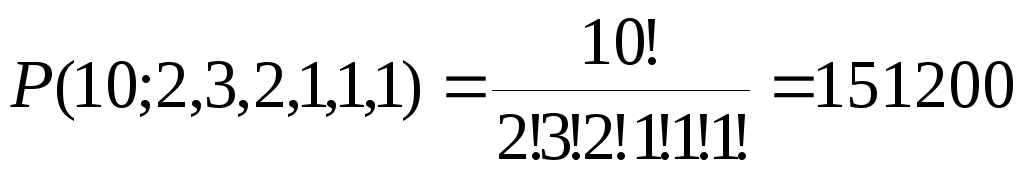 .
.
Аналогичную формулу можно получить при подсчете вариантов разбиений.
-
Разбиения и числа Стирлинга
Пусть B = {B1,…,Bk} есть разбиение множества X из n элементов на k подмножеств: i Bi X, Bi = X, Bi , Bi Bj = ij. |Bi | = ni, n1+…+nk = n. Тогда набор (B1,…,Bk) называется упорядоченным разбиением множества X, а подмножества Bi называются блоками разбиения.
Если B1 и B2 – два разбиения X, то разбиение B1 есть измельчение разбиения B2, если каждый блок B2 есть объединение блоков B1. Измельчение является частичным порядком на множестве разбиений.
Если k=2, то упорядоченное разбиение множества X на 2 подмножества, имеющие соответственно n1 и n2 элементов, определяется сочетанием (без повторений!) из n элементов по n1 и из n по n2 , n2 = n– n1. Значит, число разбиений R(n; n1, n2) равно биномиальному коэффициенту C(n, n1)=C(n, n2):
R(n;n1,n2) = ![]() .
.
-
Пусть множество X = {1,2,3,4,5,6}. B2 – разбиение его на четные и нечетные числа: B2 ={{1,3,5},{2,4,6}}, B1 = {{1,3},{5},{2},{4,6}} – измельчение разбиения B2. Теперь предположим, что X – 6 двоечников, которые 4-й раз идут сдавать физику (для удобства они идентифицированы порядковыми номерами). Преподаватель решил поделить их пополам случайным образом – блок A1 – поставить 3, блок А2 – поставить 2. Сколько различных вариантов возможно (упорядоченные разбиения множества X на 2 блока по три)? R(6;3,3)=6!/(3!·3!)=6·5·4/(3·2)=20. Выпишем все варианты: {{1,2,3},{4,5,6}}, {{1,2,4},{3,5,6}}, {{1,2,5},{3,4,6}}, {{1,2,6},{3,4,5}}, {{1,3,4},{2,5,6}}, {{1,3,5},{2,4,6}}, {{1,3,6},{2,4,5}}, {{1,4,5},{2,3,6}}, {{1,4,6},{2,3,5}}, {{1,5,6},{2,3,4}} 10 вариантов. Поскольку есть разница – попасть в А1 или в А2 (разбиения упорядоченные), то еще 10 вариантов получатся, если поменять местами первый и второй блоки разбиений. Видно, что для конкретного двоечника с номером 1 вероятность попасть в А1 или в А2 равна ½.
В общем случае, число R(n; n1,n2,
…,nk)
упорядоченных разбиений (B1, …, Bk),
для которых |Bi | = ni,
равно
![]() (сравнить с формулой 2.3):
(сравнить с формулой 2.3):
R(n; n1,n2,
…,nk)=
![]() (2.4)
(2.4)
Число
R(n,k)
упорядоченных разбиений на k
подмножеств вычисляется по формуле
R(n,k) =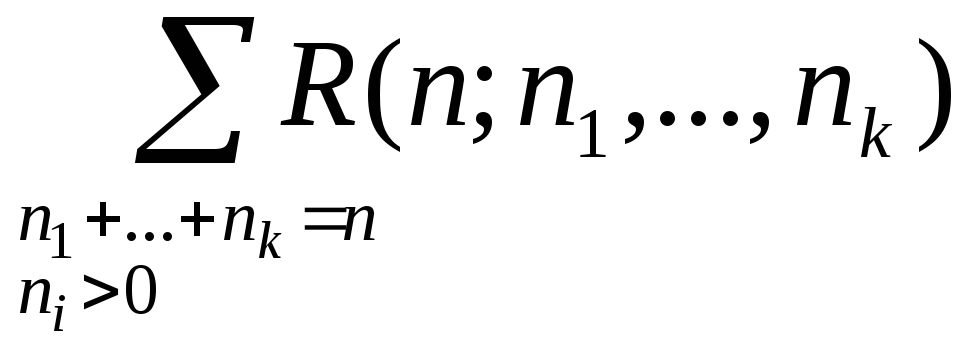 . (2.5)
. (2.5)
-
Пусть множество X = {1,2,3,4,5}. Определить количество упорядоченных разбиений его на 3 подмножества. Возможные варианты – множества по 1,1,3 элемента в разном порядке и множества по 1,2,2 (тоже в разном порядке). Их количество будет определяться согласно формулам (2.5) и (2.4): R(5,3) = R(5;1,1,3) + R(5;1,3,1) + R(5;3,1,1) + R(5;1,2,2)+ R(5;2,1,2)+ R(5;2,2,1)=(5!/3!)·3+(5!/(2!·2!))·3=3·20+3·30=150.
Числа R(n; n1, n2, …, nk) называются полиномиальными коэффициентами, поскольку для a1, a2, …, akR справедливо соотношение:
-
(Полиномиальная теорема)
(a1+a2+
…+ak )n =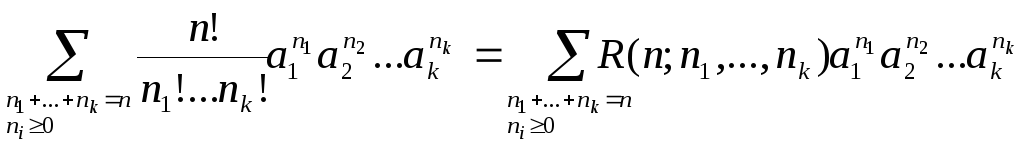 (2.6)
(2.6)
Если рассмотренный выше набор (B1,…,Bk) рассматривать без учета порядка его блоков, то он называется неупорядоченным разбиением множества X, или просто разбиением на k блоков.
-
Можно рассмотреть разбиение множества абитуриентов на несколько блоков в соответствии с количеством регистрационных столиков в приемной комиссии – все зарегистрированные за одним столиком относятся к одному блоку. Порядок безразличен разбиение является неупорядоченным.
Число разбиений n-элементного множества на k блоков называется числом Стирлинга второго рода и обозначается S(n,k). Определяются числа Стирлинга 2 рода рекурсивно следующим образом:
S(n,k)=S(n–1,k–1)+ k·S(n–1,k) (0<k<n) (2.7)
При этом S(n,0)=0 при n>0, S(n,k)=0 при n<k, S(n,n)=1, S(0,0)=1.
Из формулы 2.7 следует удобный способ рекуррентного вычисления значений чисел Стирлинга 2 рода, который можно представить в графической форме (в виде треугольника) следующим образом:
|
S(4,2) |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
|
1 |
|
1 |
|
|
|
|
2 |
|
|
|
|
|
0 |
|
1 |
|
3 |
|
1 |
|
|
|
3 |
|
|
|
|
0 |
|
1 |
|
7 |
|
6 |
|
1 |
|
|
4 |
|
|
|
0 |
|
1 |
|
15 |
|
25 |
|
10 |
|
1 |
|
5 |
-
Сколькими способами можно разбить множество {a,b,c,d} на 2 блока? Порядок значения не имеет. Тогда количество таких разбиений является числом Стирлинга 2 рода S(4,2)=S(3,1)+2·S(3,2)= 1+2·(S(2,1)+2·S(2,2))=1+2·(1+2·1) = 7. Если сравнить с приведенной таблицей, увидим тот же результат. Если выписать эти разбиения, то получим: {{a},{b,c,d}}, {{b},{a,c,d}}, {{c},{a,b,d}}, {{d},{a,b,c}}; {{a,b},{c,d}}, {{a,c},{b,d}}, {{a,d},{b,c}} – 7 подмножеств.
-
Контрольные вопросы
-
Сколько разных слов можно получить, переставляя буквы в слове «осколок»?
-
Дайте определение упорядоченного разбиения. Чем оно отличается от неупорядоченного? Имеет ли значение порядок элементов внутри блока разбиения?
-
Какую величину характеризуют числа Стирлинга второго рода?
-
Определите число неупорядоченных разбиений множества {1,2,3,4,5,6,7} на 4 блока двумя способами: используя формулу для R(7;4) и с помощью чисел Стирлинга 2 рода. Сравните результаты.
-
Чему равен коэффициент при x2y3z2 в выражении (x+y+z)7?
-
Используя полиномиальную теорему, запишите в виде многочлена выражение (3x+2y2+z3)4. Чему равен коэффициент при x2y2z3? А при y4z7?
-
Используя полиномиальную теорему, запишите в виде многочлена выражение (2x+3y2)3. Сделайте то же самое, используя формулу бинома Ньютона. Есть ли различия в результатах? Почему?
-
Найти коэффициенты при x17 и x18 в разложении (1+ x5+ x7) n.
-
Принцип включения и исключения
Рассмотренные ранее формулы и алгоритмы дают способы вычисления комбинаторных чисел для некоторых распространенных комбинаторных конфигураций. Практические задачи не всегда прямо сводятся к известным комбинаторным конфигурациям. В этом случае используются различные методы сведения одних комбинаторных конфигураций к другим.
Наиболее часто комбинаторная конфигурация является объединением других, число комбинаций в которых вычислить проще. В таком случае требуется уметь вычислять число комбинаций в объединении. В простых случаях формулы для вычисления очевидны:
-
(комбинаторный принцип сложения ):
Пусть множества A и B могут пересекаться. Тогда количество элементов, которые можно выбрать из A или B, определяется по формуле: |A B| = |A| + |B| – |A B|.
Доказательство: Множество C = AB = (A \ B) (B \ A) (AB), причем все множества в скобках являются попарно непересекающимися. Поэтому в соответствии с утверждением 2.1 |C| = |AB| = |A \ B| + |B \ A| + |AB|. Очевидно, что A = (A \ B) (AB), B = (B \ A) (AB) |A| = |A \ B| + |AB|, |B| = |B \ A| + |AB|. Значит, |A| + |B| = (|A \ B| + |AB|)+(|B \ A| + |AB|) . Правая часть утверждения теоремы имеет вид: |A| + |B| – |A B| = (|A \ B| + |AB|)+(|B \ A| + |AB|) – |A B| = |A \ B| + |AB| + |B \ A| = |AB| .
Очевидно, что рассмотренная теорема будет справедлива для произвольных множеств. Если перейти от двух множеств к большему количеству, в частности, к трем, и проиллюстрировать с помощью диаграмм Венна, то очевидным результатом явится следующая формула:
|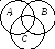 A B C| = |A| + |B| + |C| – |A B| – |A C| – |B C| + |A B C|,
т.е. для вычисления количества элементов
объединения трех множеств нужно
просуммировать мощности всех этих
множеств, вычесть мощности всех попарных
пересечений и добавить число элементов,
содержащихся в пересечении всех трех
множеств.
A B C| = |A| + |B| + |C| – |A B| – |A C| – |B C| + |A B C|,
т.е. для вычисления количества элементов
объединения трех множеств нужно
просуммировать мощности всех этих
множеств, вычесть мощности всех попарных
пересечений и добавить число элементов,
содержащихся в пересечении всех трех
множеств.
-
В месяце было 12 дождливых, 8 ветреных, 4 холодных дня, дождливых и ветреных – 5, дождливых и холодных – 3 , ветреных и холодных – 2, дождливых, ветреных и холодных – 1 день. Сколько дней была плохая погода? Пусть А – дождливые дни, В – ветреные дни, С – холодные, D – дни с плохой погодой. Тогда
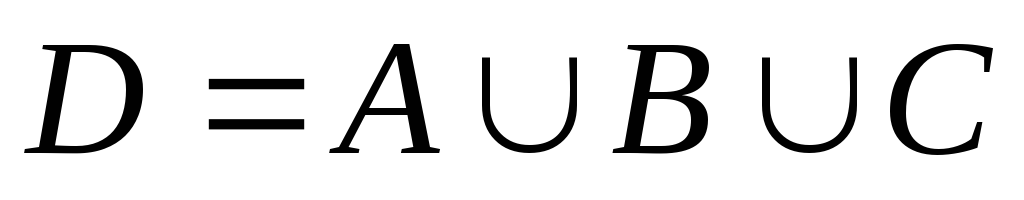 .
Количество дней с плохой погодой:
|D| = |ABC| = |A|+|B|+|C|–|AB|–|AC|–|BC|+|ABC| = 12+8+
+4–5–3–2+1 =15.
.
Количество дней с плохой погодой:
|D| = |ABC| = |A|+|B|+|C|–|AB|–|AC|–|BC|+|ABC| = 12+8+
+4–5–3–2+1 =15.
Более общая формула, известная как принцип включения и исключения, позволяет вычислить мощность объединения произвольного количества множеств, если известны их мощности и мощности всех пересечений.
-
(принцип включения и исключения):
![]()
Пусть множество А состоит из N
элементов и имеется m
одноместных отношений (свойств)
![]() .
Каждый элемент множества может обладать
или не обладать любым из этих свойств.
Обозначим через
.
Каждый элемент множества может обладать
или не обладать любым из этих свойств.
Обозначим через
![]() число элементов, обладающих свойствами
число элементов, обладающих свойствами
![]() и, может быть, некоторыми другими. Тогда
число N(0) элементов,
не обладающих ни одним из свойств
и, может быть, некоторыми другими. Тогда
число N(0) элементов,
не обладающих ни одним из свойств
![]() ,
вычисляется по следующей формуле:
,
вычисляется по следующей формуле:
![]() ,
где
,
где
![]()
Обобщая,
получаем формулу, позволяющую вычислить
число N(r)
элементов, обладающих ровно r
свойствами
![]() .
.
![]() (2.8)
(2.8)
Определим
функцию [x]
для вещественных чисел как наибольшее
целое число, не превосходящее x.
Число [x]
называется целой
частью числа
x.
Для положительных чисел а
и b
значение функции
![]() равно количеству чисел из множества
{1, 2,…, b},
которые делятся на а,
т.е. кратны а.
равно количеству чисел из множества
{1, 2,…, b},
которые делятся на а,
т.е. кратны а.
-
Сколько положительных трехзначных чисел делятся ровно на одно из чисел 3, 5 или 7? Обозначим P3 – свойство делимости на 3, P5 – на 5, P7 – на 7. Всего трехзначных чисел 9·10·10=900. Тогда
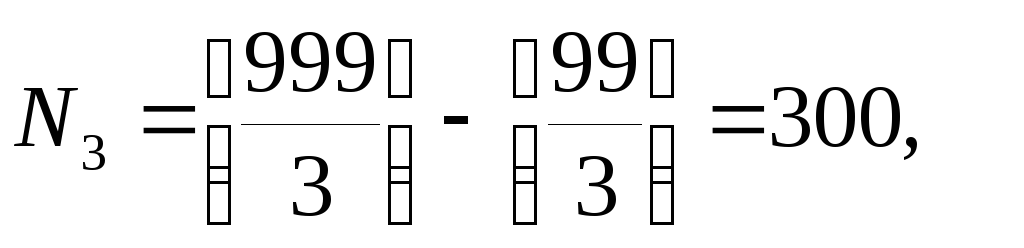
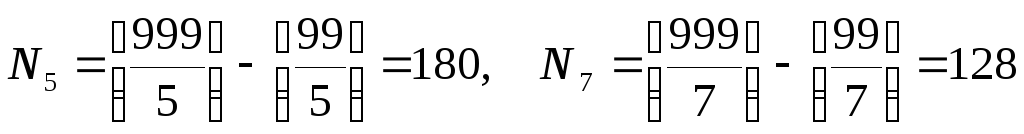 .
.
Так как N3,5
– число чисел, делящихся одновременно
на 3 и 5, а наименьшее общее кратное 3 и 5
равно 15, то
![]() .
Аналогично,
.
Аналогично,
![]()
![]() По формуле (2.8) находим искомое число:
По формуле (2.8) находим искомое число:
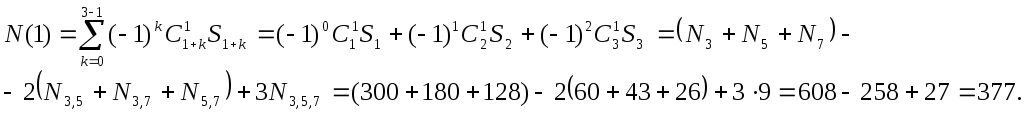
Контрольные вопросы
-
Подсчитайте, сколько чисел в диапазоне от 1 до 100 делятся на 3? На 3 или 5? На 6 или 9? Только на одно число из двух – или на 6, или на 9?
-
Рекуррентные функции
-
Понятие рекуррентного соотношения
Понятие последовательности было введено в разделе «специальные функции».
Рекуррентным
соотношением, рекуррентным уравнением
или рекуррентной формулой называется
соотношение вида
![]() ,
которое позволяет вычислить все члены
последовательности
,
которое позволяет вычислить все члены
последовательности
![]() ,
если заданы ее первые k
членов.
,
если заданы ее первые k
членов.
-
1. Формула an+1 = an+d задает арифметическую прогрессию. 2. Формула an+1 = qan задает геометрическую прогрессию. 3. Формула an+2 = an+1+an задает последовательность чисел Фибоначчи.
В случае, когда рекуррентное соотношение
линейно и однородно, т.е. для всех n
и некоторого k
выполняется
![]() (2.9)
где pi = const,
последовательность a0, a1,…
называется возвратной. Соотношение
(2.9) называется возвратным уравнением
порядка k.
(2.9)
где pi = const,
последовательность a0, a1,…
называется возвратной. Соотношение
(2.9) называется возвратным уравнением
порядка k.
-
Геометрическая прогрессия – это возвратная последовательность первого порядка, так как an+1 =qan an+1 –qan=0.
-
Арифметическая прогрессия задается рекуррентным соотношением an+1 =an + d an+1 – an = d Данное уравнение не является однородным, попробуем привести его к однородному виду. Выпишем an+2 –an+1 = d и приравняем левые части выражений. Получим an+2 – an+1 = an – an+1 an+2 –2 an+1 – an = 0 это возвратная последовательность второго порядка.
Если
переписать уравнение (2.9) в виде
![]() и задать n=0, то получим:
и задать n=0, то получим:
![]() действительно,
зная первые k членов,
можно из рекуррентного соотношения
получить любой член возвратной
последовательности. Поскольку эти
первые k членов можно
выбирать бесконечным числом различных
способов, то существует также бесконечное
множество последовательностей,
удовлетворяющих уравнению (2.9).
действительно,
зная первые k членов,
можно из рекуррентного соотношения
получить любой член возвратной
последовательности. Поскольку эти
первые k членов можно
выбирать бесконечным числом различных
способов, то существует также бесконечное
множество последовательностей,
удовлетворяющих уравнению (2.9).
-
Решение рекуррентного уравнения
Любая последовательность, удовлетворяющая возвратному уравнению, называется его решением.
-
Арифметические прогрессии 5,7,9,11,…; 2,6,10,14,… удовлетворяют возвратному уравнению an+2 –2 an+1 –an = 0 являются его решениями.
Произведением числа на последовательность {xi} называется последовательность {xi}, каждый член которой получен умножением соответствующего члена последовательности {xi} на .
Суммой последовательностей {xi} и {yi} называется последовательность, каждый член которой {xi + yi} равен сумме соответствующих членов последовательностей {xi} и {yi}.
Из определений суммы и произведения следует, что линейная комбинация последовательностей также является последовательностью.
Утверждение 2.4. Если возвратные
последовательности {ai(1)},
{ai(2)},
…,{ai(s)}
удовлетворяют уравнению
![]() то этому уравнению удовлетворяет также
последовательность {1ai(1)
+2ai(2)
+…+ sai(s)}.
то этому уравнению удовлетворяет также
последовательность {1ai(1)
+2ai(2)
+…+ sai(s)}.
Многочлен
P(x)=![]() (2.10)
называется характеристическим
для возвратной последовательности
{an}.
Корни многочлена P(x)
называются характеристическими
корнями.
(2.10)
называется характеристическим
для возвратной последовательности
{an}.
Корни многочлена P(x)
называются характеристическими
корнями.
Множество всех последовательностей, удовлетворяющих данному рекуррентному соотношению, называется общим решением.
Общее решение рекуррентного соотношения находится по аналогии с общим решением однородного дифференциального уравнения с постоянными коэффициентами.
-
(о корнях характеристического многочлена):
1. Пусть – корень характеристического многочлена (2.10). Тогда последовательность {cn}, где c – произвольная константа, удовлетворяет соотношению (2.9).
2. Если i
– простые корни (i = 1,…,k)
многочлена (2.10), то общее решение
соотношения (2.9) имеет вид
![]() где ci
= const (i=1,…,k).
где ci
= const (i=1,…,k).
3. Если i
– корень кратности ri
(i =1, …, s),
то общее решение имеет вид
![]() ,
где
,
где
![]() – произвольные константы (i=1,…,n,
j=1,…,ri).
– произвольные константы (i=1,…,n,
j=1,…,ri).
Зная
общее решение рекуррентного соотношения,
по начальным условиям a0
,a1,…
можно найти неопределенные постоянные
![]() и
тем самым получить частное решение
рекуррентного уравнения с данными
начальными условиями.
и
тем самым получить частное решение
рекуррентного уравнения с данными
начальными условиями.
-
Найти последовательность {an}, удовлетворяющую рекуррентному соотношению
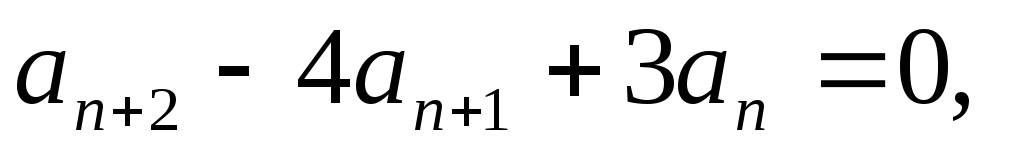 и
начальным условиям:
и
начальным условиям:
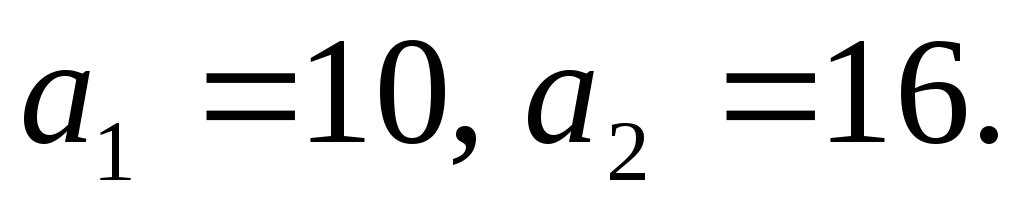 Составим
характеристический многочлен
Составим
характеристический многочлен
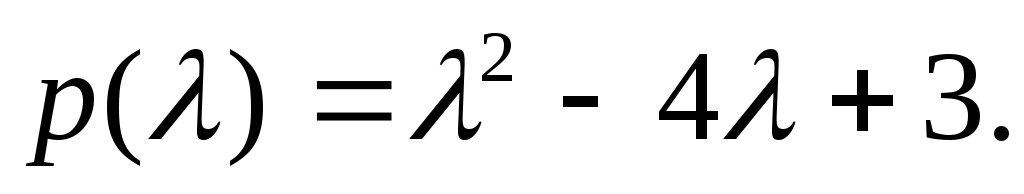 Его корнями являются числа
Его корнями являются числа
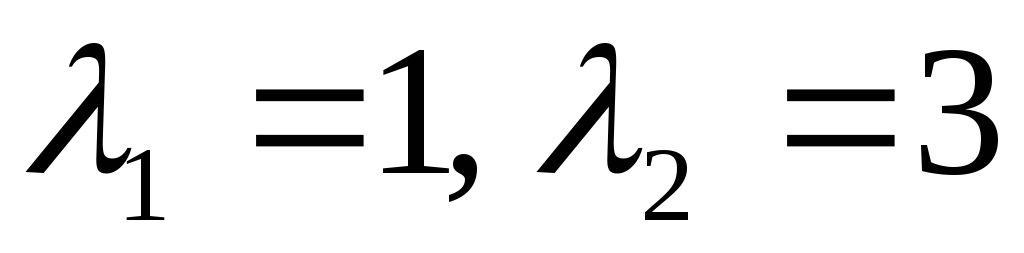 .
Следовательно, общее решение рекуррентного
соотношения имеет вид:
.
Следовательно, общее решение рекуррентного
соотношения имеет вид:
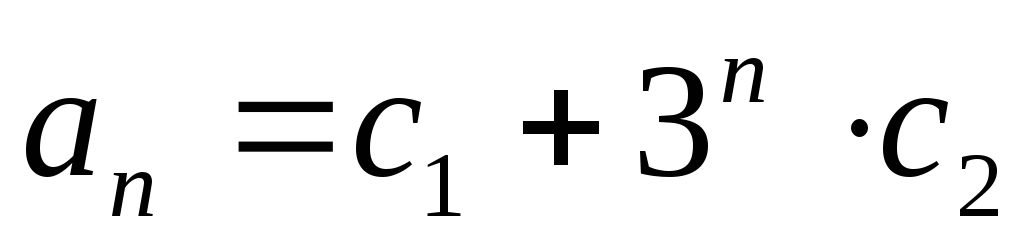 .
Используя начальные условия, получим
систему:
.
Используя начальные условия, получим
систему:
 из которой находим c1
=7, c2 =1
из которой находим c1
=7, c2 =1
 an
= 7+ 3n.
an
= 7+ 3n.
-
Найти последовательность {an}, удовлетворяющую рекуррентному соотношению
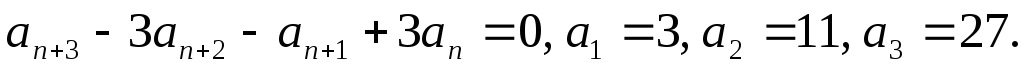 Составим
характеристический многочлен
Составим
характеристический многочлен
 Для нахождения корней сгруппируем
слагаемые
Для нахождения корней сгруппируем
слагаемые
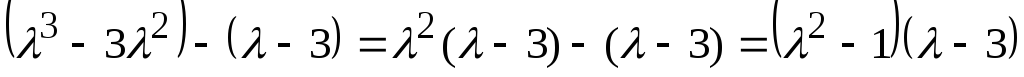 .
Составим характеристическое уравнение
.
Составим характеристическое уравнение
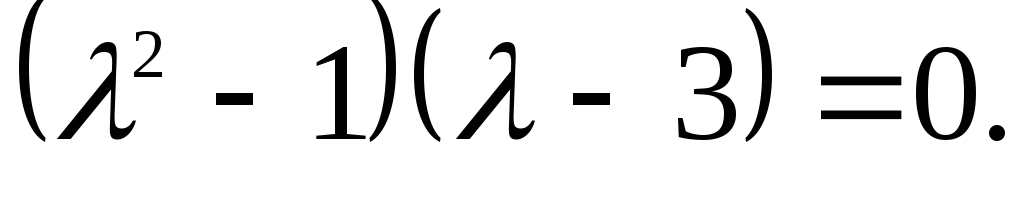 Его корнями являются числа
Его корнями являются числа
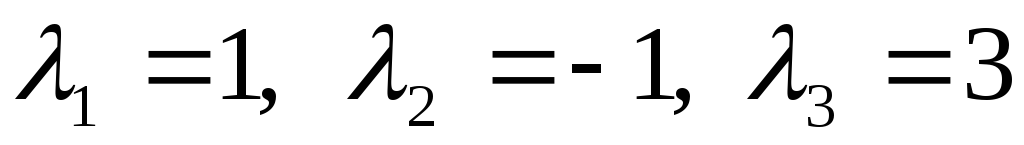 .
Все корни простые. Следовательно, общее
решение рекуррентного соотношения
имеет вид:
.
Все корни простые. Следовательно, общее
решение рекуррентного соотношения
имеет вид:
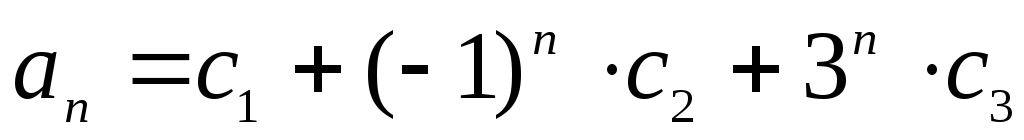 .
Используя начальные условия, получим
систему:
.
Используя начальные условия, получим
систему:
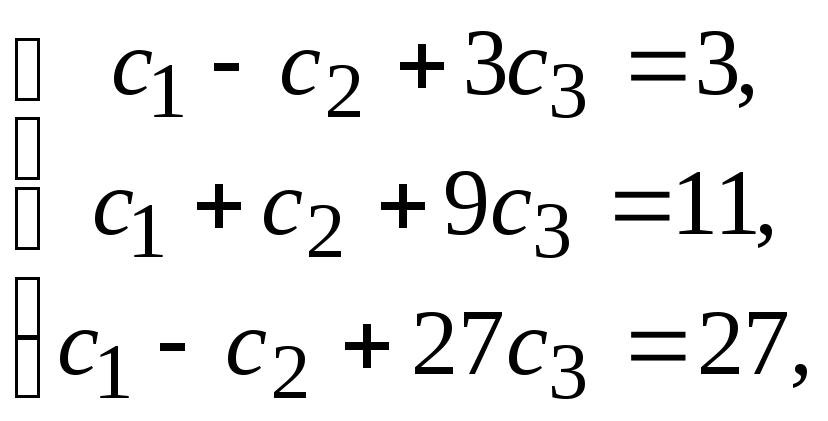 решая которую находим с1=1,
с2= 1, с3=1.
Таким образом,
решая которую находим с1=1,
с2= 1, с3=1.
Таким образом,
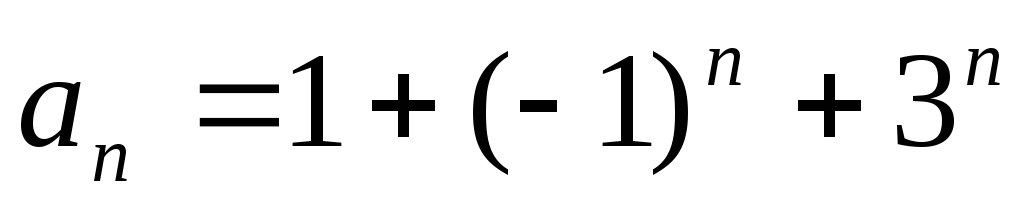 .
.

 этом равнобедренном треугольнике
каждое число (кроме боковых единиц)
является суммой двух стоящих над ним
чисел. Тогда число сочетаний C(n,k)
находится в (n+1)
ряду на (k+1)
месте.
этом равнобедренном треугольнике
каждое число (кроме боковых единиц)
является суммой двух стоящих над ним
чисел. Тогда число сочетаний C(n,k)
находится в (n+1)
ряду на (k+1)
месте. В
этом треугольнике каждое k-е
в ряду число является суммой левого
стоящего над ним числа с правым,
умноженным на k. Тогда
число Стирлинга S(n,k)
находится в n–м
ряду на k-м месте,
если начинать счет от 0.
В
этом треугольнике каждое k-е
в ряду число является суммой левого
стоящего над ним числа с правым,
умноженным на k. Тогда
число Стирлинга S(n,k)
находится в n–м
ряду на k-м месте,
если начинать счет от 0.