Функция распределения
Функцией распределения случайной величины Х называют вероятность того, что она примет значение меньше некоторого действительного числа х. Обозначают
Геометрически функцию распределения можно интерпретировать следующим образом: пусть значения случайной величины обозначаются точками М оси ОХ и точка N(x, 0) произвольная точка с абсциссой х. Тогда функция F(x) это вероятность того, что наудачу брошенная на числовую прямую точка М окажется левее точки N.
Пример 1. В условиях примера 2. предыдущего пункта построить функцию распределения случайной величины Х – числа попаданий в мишень обоими стрелками.
Решение: Будем пользоваться определением и геометрическим представлением функции распределения.
Пусть:
,
тогда
,
так как значений Х меньше числа 0 просто
нет.
Если
,
то меньше числах
принимается только одно значение
.
Значит
.
Если
,
то левее числах
лежит уже два значения
и
.
Следовательно,
.
Если
,
то
=
= 0,8 + 0,2 = 1, т.е. F(x) = 1. Итак:
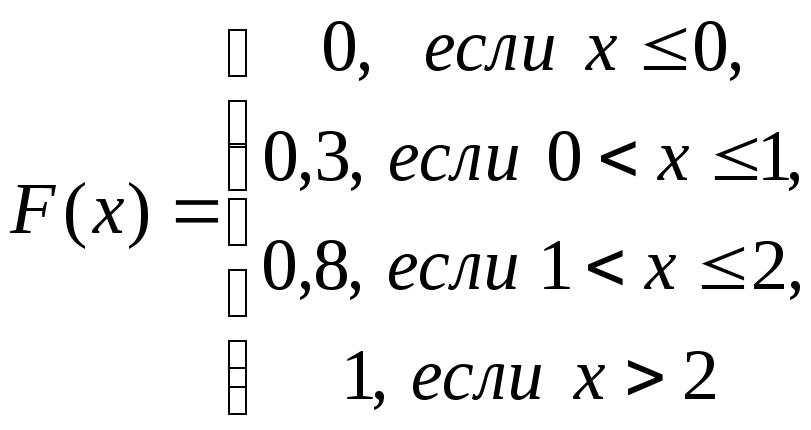
Свойства функции распределения
1. Функция распределения принимает значения на промежутке [0,1]
2. Функция F(x) – неубывающая функция:
Пусть
.
Рассмотрим следующие события
Тогда
и
.
Учитывая, что
,
получим
,
что и доказывает неравенство:
.
3. Справедливо
равенство:
4.
5. Функция распределения имеет не более счетного множества точек разрыва, причем только «скачков».
6. В каждой точке разрыва функция распределения непрерывна слева.
Замечание: каждая функция распределения удовлетворяет перечисленным свойствам. Верно и обратное, если функция удовлетворяет указанным свойствам, то она может рассматриваться как функция распределения некоторой случайной величины.
При этом надо иметь ввиду, что если случайная величина однозначно определяет свою функцию распределения, то существует сколь угодно случайных величин имеющих данную функцию распределения. Например, если случайная величина Х принимает два значения 1 или -1 с вероятностями 0,5, то случайная величина Y = -X, также принимает значения -1 и 1 с вероятностями 0,5. Однако, ясно, что Y всегда отлична от Х. Не трудно проверить, обе случайные величины имеют одну и туже функцию распределения
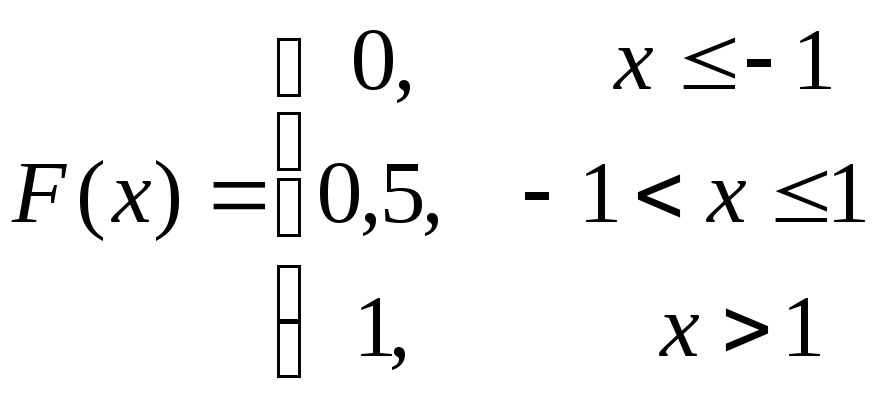
Из определения дискретной случайной величины следует, что её функция распределения имеет вид
.
Математическое ожидание и дисперсия дискретной случайной величины
Пусть дискретная случайная величина имеет распределение
-
Х
х1
х2
…
xn
Р
p1
p2
…
pn
Математическим ожиданием называют число равное сумме произведений значений случайной величины на соответствующие вероятности. Обозначают
Если случайная величина принимает счетное множество значений, то математическое ожидание есть сумма ряда
.
Прежде чем рассматривать свойства математического ожидания, определим операции над случайными величинами.
1. Произведением случайной величины Х на число k назовем новую случайную величину kX, значения которой равны значениям исходной случайной величины Х умноженные на число k и принимаются с теми же вероятностями.
2. Квадратом случайной величины Х называют новую случайную величину Х2, значения которой равны квадратам значений случайной величины Х и принимаются с теми же вероятностями.
При этом надо иметь в виду, что в результате возведения в квадрат некоторые значения становятся одинаковыми. В этом случае новое значение записывают один раз, а соответствующие вероятности складывают.
|
X2 |
0 |
4 |
16 |
|
P |
0,25 |
0,5 |
0,25 |
|
X |
-2 |
0 |
2 |
4 |
|
P |
0,15 |
0,25 |
0,35 |
0,25 |
3. Суммой двух случайных величин Х и Y называют новую случайную величину, значения которой равны всевозможным значениям величин Х и Y, а соответствующие вероятности перемножаются, если X и Y независимы. В случае зависимости случайных величин вероятность значения X умножается на условную вероятность значения Y. При этом так же новые значения могут повторяться. Их записывают один раз, а вероятности повторяющихся значений складывают.
Рассмотрим задачу: Два баскетболиста по очереди забрасывают мяч в корзину. Всего сделано пять бросков. Вероятность попадания при одном броске первым баскетболистом равна 0,8, вторым – 0,9.
Составить таблицу распределения числа попаданий в корзину обоими баскетболистами.
Решение: Обозначим число попаданий первым баскетболистом через Х, вторым – Y. Первый игрок, согласно условию задачи, сделает три броска, второй – 2. Поскольку результаты бросков не зависят друг от друга, то мы находимся в условиях схемы Бернулли, и вероятности значений случайных величин Х и Y будем подсчитывать по формуле Бернулли
После не сложных вычислений, получим следующие распределения случайных величин Х и Y:
|
Х |
0 |
1 |
2 |
|
P |
0,01 |
0,18 |
0,81 |
|
Х |
0 |
1 |
2 |
3 |
|
P |
0,008 |
0,096 |
0,384 |
0,512 |
Для построения суммы, составим таблицу:
|
X |
Y |
X+Y |
Pij |
|
X |
Y |
X+Y |
Pij |
|
0 |
0 |
0 |
0,00008 |
|
2 |
0 |
2 |
0,00384 |
|
0 |
1 |
1 |
0,00144 |
|
2 |
1 |
3 |
0,06912 |
|
0 |
2 |
2 |
0,00648 |
|
2 |
2 |
4 |
0,31104 |
|
1 |
0 |
1 |
0,00096 |
|
3 |
0 |
3 |
0,00512 |
|
1 |
1 |
2 |
0,01728 |
|
3 |
1 |
4 |
0,09216 |
|
1 |
2 |
3 |
0,07776 |
|
3 |
2 |
5 |
0,41472 |
Составим теперь новую таблицу распределения суммы, записывая каждое значение по одному разу. Вероятности повторяющихся значений будем складывать:
|
X+Y |
0 |
1 |
2 |
3 |
4 |
5 |
|
P |
0,00008 |
0,0024 |
0,0276 |
0,152 |
0,4032 |
0,41472 |
4. Произведением двух независимых случайных величин называется новая случайная величина, значения которой равны всевозможным значениям случайных величин X и Y, при этом соответствующие вероятности перемножаются.