L03-Динамика, законы сохранения

Величину

U

можно определять

с

al

точностью

до

неизвестной

аддитивной

постоянной

i

U0, поскольку

t

это никак не повлияет на результат вычисления силы.

n

Получим связь U

de

с силой. Мы знаем, что работа на

пути ds равна dA = Fds = Fxdx , если движение идет

i

f

вдоль оси Х. Приравняем эту работу убыли

потенциальной энергии

dA = Fxdx = −dU (см.

A12 =U1 −U2 )

C

Отсюда Fx

= − dU

on

dUy

dx

Если есть движение и по другим направлениям, то

F = − dU

,

F = −

dy

F = − dU

и

F = - dU e

- dU e

- dU e

z ,

x

dx

y

z

dz

dx

x

dy

xy

dz

что может быть переписано как

F=-ÑU(x,y,z) ,

где

m

Ñ = -

d

e

-

d

e -

d

e

- оператор набла – он выполняет

o

pan

dx

x

dy

y

dz

z

операцию градиента.

Итак, сила равна градиенту потенциальной энергии с

Cотрицательным знаком.

равна

A12 = mg(h1 − h2 ) = U1 −U2

al

Это означает, что U = mgh , где h отсчитывается от

произвольного уровня.

i

t

Пусть

на частицу

кроме

n

сил

консервативных

de

Тогда

действуют еще и неконсервативная сила F*.

работа

на

участке

i

1-2

равна

A =U −U

2

+ A

= T

−T

Поскольку

12

1

12

2

1

E2 − E1 =

on

−U1

и если T2 = T1 ,

T +U = E , то

A12

= U2

то работа неконсервативных сил идет на приращение

потенциальной энергии.

y

Если система состоитCиз N невзаимодействующих

частиц находящихся в поле консервативных сил, то

для каждой

частицы

Ti +Ui

= Ei = consti

и

после

суммирования

получаем E = const .

Это

означает

m

аддитивность полной механической энергии системы

невзаимодействующихpan

частиц в поле консервативных

o

сил и выражает закон сохранения энергии для

C

невзаимодействующих частиц.

(например, во внутреннюю, в тепло).

Такой процесс

al

называется диссипацией (рассеянием) энергии, а силы

i

к этому приводящие – диссипативны. Строго говоря,

t

все системы в природе являются диссипативными.

n

§ 24. Потенциальная энергия взаимодействия

Пусть

теперь

система

состоит

из

двух

f

F

= -F

взаимодействующих

частиц

i

по

с силойde12

21

третьему

закону

Ньютона. Расстояние между

частицами R12

C

r2

и r1 - радиусы-векторы

= r2 -r1

, где

частиц.

Пусть

силы

зависятonтолько

от

расстояния

y

между частицами и направлены вдоль прямой

соединяющей

частицы

(гравитационное

или

pan

кулоновское взаимодействие).

Тогда F12

= f (R12 )e12

и F21 = − f (R12 )e12

Если система замкнута и нет внешних сил, то

уравнения движения

C

m v&

= F

m v&

= F

1m1

12

и

2

2

21

o

на

dr = v dt

и

dr = v

dt

,

Умножаем их

1

1

2

2

Подставим

силы

и

получим

dAвнутр = F12dr1 + F21dr2

= f (R12 )e12dr1 − f (R12 )e12dr2

= − f (R12 )e12dR12

al

В результате получаем, что приращение кинетической

i

энергии dT равно работе внутренних сил dAвнутр

за это

n

время или dT= - dU.

t

Последнее означает, что d(T+ U)= dE=0 или

E=T+U для рассматриваемой системы

сохраняется.

f

Здесь функция U (R12 ) - потенциальная энергия

взаимодействия частиц и она зависитideот расстояния

между частицами.

on

§ 25. Закон сохранения энергии

y

Cведем все результатыCвместе и получим закон

pan

сохранения энергии. Для этого рассмотрим систему

из N материальных точек c массами m1, m2, …mN,

движущихся со скоростями v1, v2, … vN. Пусть

частицы взаимодействуют друг с другом с силами Fik,

m

модули которых зависят только от расстояния Rik

между частицами. Такие силы консервативны. Кроме

o

внутренних сил на каждую частицу i действует

C

и внешняя

внешняя консервативная сила Fi

неконсервативная сила Fi*. Тогда уравнение движения

i частицы имеет вид уравнения второго закона

Ньютона:

dvi

N

mi

= å Fik + Fi + F*i

dt

k =1(k ¹i)

åmi vidvi = å

N

( å Fik )dri + åFi dsi + åF*i dsi

i

i

k =1(k ¹i)

i

i

Левая часть

–

приращение

кинетической энергии

m v 2

al

системы

åmi vidvi = då

i i

= dT

i

i

i

2

n

Первый

член

правой

части

–

равенtубыли

de

потенциальной энергии взаимодействия частиц

N

N

i

N

å (

å

Fik )dri

= − å Fik dRik

= −

å Uik (Rik ) = −dUвзаим

i

k=1(k¹i)

k=1(k¹i)

f

=1(k¹i)

on

k

Второй член правой части – равен убыли

потенциальной

энергии

системы

во

внешнем поле

i

i

C

консервативных сил

åFidsi = d åUi

(ri ) = −dU

внешн

y

pan

Третий член правой части – работа неконсервативных

внешних сил

åF idsi

= ådA i = dA внешн

i

i

o

d(T +U +U ) = dA

C

m

взаим

внешн

внешн

Таким образом

где

T +Uвзаим +Uвнешн = E

есть полная

механическая

механическая энергия системы, на которую

действуют только консервативные силы, остается

постоянной.

ial

Для замкнутой системы T +Uвзаим

t

= E = co st

n

При движении тела в замкнутой консервативной

системе

происходит

непрерывное

превращение

i

de

и обратно

кинетической его энергии в потенциальнуюf

в эквивалентных количествах, так что полная энергия

остается

неизменной.

Закон

сохранения

и

превращения

энергии

- фундаментальный закон

природы,

он

on

для

систем

справедлив как

C

микроскопических тел, так и для систем микротел.

y

В замкнутой системе, в которой действуют силы

трения, полная механическая энергия системы при

движении убывает. Следовательно, в этих случаях

закон

сохранения

механической

энергии

pan

Однако

при

«исчезновении»

несправедлив.

механическойm

энергии

всегда

возникает

oэквивалентное количество энергии другого вида.

C

§ 26. Энергия упругой деформации

В случае отдельно взятого упруго деформированного

тела потенциальной энергией обладают ее части. Эта

энергия

зависит

от взаимного

расположения

отдельных ее частей.

al

i

t

Для деформирования пружины необходимо затратить

2

2

n

работу

A = kx

,

которая идет

de

на увеличение

i

f

потенциальной энергии пружины U = kx2 .

on

2

C

y

pan

m

o

C

системы может быть определено с помощью только

одной величины, например координаты х. В качестве

al

примера можно привести шарик, скользящий без

i

трения по укрепленной неподвижно изогнутой

проволоке

(рис.

а). На

шарик

действует

консервативная сила тяжести

n

de

t

i

f

on

C

y

pan

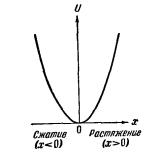
График потенциальной энергии как функции U(x)

показан на рис. б.

Поскольку шарик движется без трения, то сила,

C

на него со стороны

проволоки,

действующаяm

oперпендикулярна к

скорости

шарика и

работы не

Кинетическая энергия может возрасти только за счет

убыли потенциальной. Поэтому если скорость шарика

равна нулю, а потенциальная энергия минимальна, то

он будет находиться в состоянии равновесия – без

воздействия со

стороны он не сможет

прийти в

движение.

al

dU

i

t

Минимумам U соответствуют значения х, равные х0 .

В этом случае dx

= 0

n

, что равнозначно Fx

=

0 .

Таким

образом,

de

системы,

f

конфигурация

соответствующая минимуму потенциальнойi

энергии,

обладает тем свойством, что силы, действующие на

тела системы, равны нулю. Этот результат остается

C

справедливым и в общем случае, когда U является

функцией нескольких переменныхon .

y

В случае, изображенном на рис. условие равенства

нулю потенциальной энергии также для х, равного х0’

(т. е. для максимума). Определяемое этим значением

х положение шарика также будет равновесным.

m

Однако это равновесие в отличие от равновесия при х

= х0 будетpanнеустойчивым: достаточно слегка вывести

o

C

шарик из этого положения, как возникает сила,

Если полная энергия системы

имеет

значение,

соответствующее

проведенной

на

al

графике

i

горизонтальной черте, то система может совершать

движение либо в пределах от х0 до x2 или в пределах

n

от х3 до бесконечности. В область х < x1 и tх2 < х < х3

de

система проникнуть не может, так как потенциальная

энергия не может стать больше полной энергии (если

бы это случилось, то кинетическая энергия стала бы

f

отрицательной).

i

Таким образом, область х2< х <х3 представляет собой

C

потенциальный барьер, через который система не

может проникнуть, имеяonданный запас полной

энергии.

y

§ 28. Закон сохранения количества движения

m

(импульса)

Найдем еще одну аддитивную сохраняющуюся

величинуpanдля замкнутой механической системы.

o

Рассмотрим механическую систему, состоящую из N

C

частиц, масса и скорость

взаимодействующих