
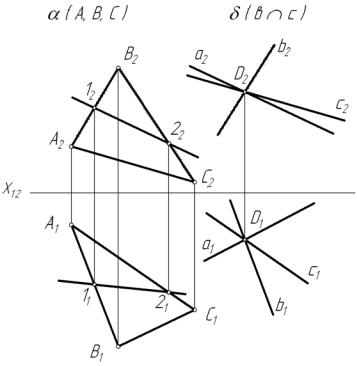
На рис. 40 задана плоскость общего положения α (А1 |
,В1 ,С1 ; А2 , В2 |
, С2 |
) |
|
и точка D (D1 , D2 ), не принадлежащая плоскости. Через |
точку |
D (D1 |
, D2 |
) |
построена прямая а (а1 , а2 ). Требуется проверить: параллельна ли |
прямая |
|||
а плоскости α; построить инцидентную точке D прямую b (b1 b2), парал- |
||||
лельную α .
Рис. 40
Для решения задачи применяем условие параллельности прямой
плоскости. В пло скости строим прямую 1, 2 (12 , 22 ; 11 , 21 ). При этом обеспечиваем условие (12 ; 22 ) || а2 . Остается проверить соблюдение условия (11 ; 21 ) || а1 . Если условие соблюдено, то прямая а || α (А, В, С ), и нет в противном случае. На рис. 40 прямая а не параллельна α .
Для построения прямой, параллельной α, строим ее проекции параллельными какой-либо прямой, инцидентной α . На рис. 40 построена прямая с || АС. Кроме того, построена прямая b || АВ. Пересекающиеся прямые
b и с задают плоскость δ (b с), параллельную плоскости α (А, В, С ).
4.1. Способы преобразования чертежа
Рассмотрим способы преобразования чертежа. Речь идёт о чертежах, состоящих из ортогональных проекций, которые мы будем называть исходными. Исходные чертежи не всегда содержат проекции, удобные для решения конкретной задачи. Сравним, например, рис. 39 и рис. 38, в. Решается одна и та же задача построения истинного расстояния от точки
45
до плоскости. На рис. 38, в задана проецирующая плоскость, и этот чертеж очень удобен для решения задачи. Чертеж на рис. 39 той же задачи требует применения многих приёмов и операций. Нельзя ли задать преобразование, которое бы изменяло исходный чертеж в направлении увеличения простоты и эффективности решения конкретной задачи?
Под преобразованием чертежа будем понимать построение допол-
нительных к исходному чертежу проекций того же оригинала, на которых решение поставленной задачи либо упрощается, либо содержит решение в явном виде.
Здесь весьма существенным является условие неизмененности на дополнительных проекциях исходного для них оригинала. Другими словами исходное и преобразованное изображение должны быть изображениями одного и того же оригинала. Оригинал характеризуется параметрами формы и величины, независимыми от его положения в пространстве. Представляется очевидным, что форма и величина оригинала не изменится, если останутся постоянными расстояния между любыми парами точек оригинала. Другими словами не изменится метрика.
Переходя к чертежу, можно применить способ прямоугольного треугольника, устанавливающий метрику трехмерного пространства на чертеже.
Пусть задан оригинал, в котором имеются поименованные пары точек, характеризующие параметры формы и величины оригинала. Истинные расстояния между парами этих точек после проецирования оригинала в чертеж устанавливаются с помощью построения прямоугольных треугольников. Катеты этих треугольников являются основой для их построения. Если построить проекции этого оригинала, то можно определить истинные расстояния между любыми точками оригинала, используя его проекции. Если необходимо построить другую проекцию того же оригинала, то эти расстояния не должны измениться. При этом оригинал может перемещаться в пространстве относительно плоскости проекций. Либо плоскость проекций может изменять положение относительно оригинала.
Приведем простейшие примеры преобразования исходного чертежа. Пусть на рис. 41, а задан исходный чертеж отрезка прямой общего положения АВ (А1 , В1 ; А2 , В2 ). Требуется построить преобразованную проекцию, содержащую истинную длину отрезка АВ.
На рис. 41, а задача решена путем перемещения исходного отрезка в положение параллельного плоскости П2 . При этом сохранены параметры формы горизонтальной проекции отрезка и расстояния от концов фронтальной проекции до оси 0х, то есть величины катетов прямоугольного
46
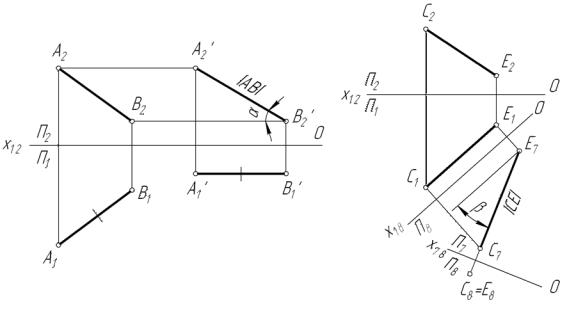
треугольника, гипотенуза которого равна длине исходного отрезка. В новом положении отрезок проецируется на плоскость П2 без искажения. Задача решена.
а |
б |
|
Рис. 41 |
На рис. 41, б аналогичная задача относительно отрезка СЕ решена методом проецирования неподвижного исходного отрезка на новые плоскости проекций П 7 и П 8 . Первая из них выбирается параллельной проекции С1 Е1 отрезка. Проекция С7 Е7 строится из расчёта сохранения расстояний проекции С2 Е2 до оси 0х.
Легко заметить, что и в этом случае катеты прямоугольного треугольника сохраняются, и новая проекция С7 , Е7 является изображением того же исходного отрезка СЕ.
Плоскость П8 выбрана перпендикулярной исходному отрезку, т.к. ось х7 перпендикулярна С7 , Е7 (соблюдено условие теоремы). В результате отрезок спроецировался на П8 в точку.
На рис. 42 решена задача построения истинной фигуры треугольника АВС двумя приведёнными выше методами, а именно: на рис. 42, а – методом плоско-параллельного перемещения, а на рис. 42, б – методом замены плоскостей проекций. Легко заметить, что в обоих случаях при построении преобразованного чертежа одна из проекций сохраняет свою форму и величину. От другой проекции берутся расстояния от точек до осей проекций, разделяющих соответствующие пары проекций.
47

а б
Рис. 42
На рис. 43 показано решение аналогичной задачи вращением исходной фигуры треугольника около оси, в качестве которой взята горизонталь А1 ,11 . При вращении треугольника АВС около горизонтали точки В и С описывают окружности, которые на горизонтальной плоскости П2 проецируются в прямые, перпендикулярные горизонтальной проекции горизонтали А1 ,11 .
Проекция радиуса вращения точки В есть отрезок В2 К2 . При повороте треугольника в положение параллельного плоскости П1 этот отрезок превращается в истинный радиус вращения
B 1 К1 . Истинная величина этого радиуса построена методом прямоугольного треугольника. Поскольку точки А и 1 остаются при вращении на месте как принад-
лежащие оси вращения, точка C находится из условия, что точки В1 ,11 и С1 лежат на одной прямой. Это условие при вращении не из-
Рис. 43 меняется.
48
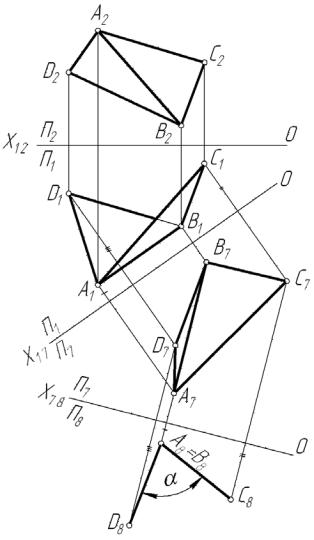
На рис. 44 показана задача построения линейного угла, измеряющего двугранный угол А, В, С, D с ребром АВ. Введены плоскости проекций П7 и П8 , при проецировании на которые ребро двугранного угла, отрезок АВ, проецируется в точку (см. чертеж рис. 41, б). В этом положении линейный угол проецируется в истинную величину α.
Рис. 44
Наконец, рис. 45, 46 и 47 демонстрируют решение задач на определение истинных расстояний между фигурами.
49
|
|
|
|
|
|
|
|
|
|
|
|
|
|
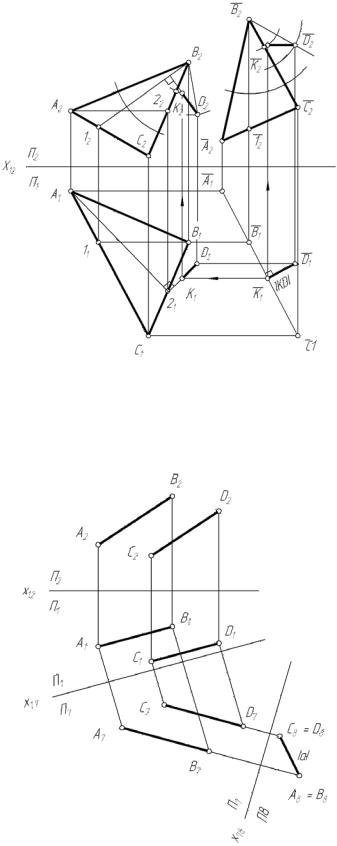
На рис. 45 исходными |
|||||||
|
|
|
|
|
|
|
|
|
|
являются |
плоскость |
общего |
|||||||||
|
|
|
|
|
|
|
|
|
|
положения γ (А,В,С) |
|
и |
точка |
||||||||
|
|
|
|
|
|
|
|
|
|
D. Требуется определить ис- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
тинное расстояние от точки D |
|||||||||||
|
|
|
|
|
|
|
|
|
|
до плоскости γ. Для решения |
|||||||||||
|
|
|
|
|
|
|
|
|
|
задачи в плоскости построе- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
на |
горизонталь |
|
А, 2 и |
||||||||
|
|
|
|
|
|
|
|
|
|
фронталь В, 1 . Произведено |
|||||||||||
|
|
|
|
|
|
|
|
|
|
преобразование |
чертежа ме- |
||||||||||
|
|
|
|
|
|
|
|
|
|
тодом перемещения. Конфи- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
гурация А, |
В, С, D перемещена |
||||||||||
|
|
|
|
|
|
|
|
|
|
в новое положение так, что |
|||||||||||
|
|
|
|
|
|
|
|
|
|
фронтальная проекция В2 , 12 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
фронтали в новом положе- |
|||||||||||
|
|
|
|
|
|
|
|
|
Рис. 45 |
нии стала перпендикулярной |
|||||||||||
|
|
|
|
|
|
|
|
|
оси x12 . В результате плос- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
кость |
|
|
γ (А, В, С) стала горизонтально-проецирующей |
и |
ее |
|
проекция |
||||||||||||||
|
|
( |
|
|
, |
|
1 , |
|
1 ) стала прямой линией. Опустив перпендикуляр из |
|
1 на эту |
||||||||||
|
γ |
А |
1 |
В |
С |
D |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
прямую, получаем истин- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
ное расстояние от D до |
|||||||||||
|
|
|
|
|
|
|
|
|
|
плоскости γ (А, В, С), отрезок |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 , |
|
1 . Используя построе- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
K |
D |
|||||||||
|
|
|
|
|
|
|
|
|
|
ния, показанные стрелками, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
находим проекции искомого |
|||||||||||
|
|
|
|
|
|
|
|
|
|
расстояния на исходном чер- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
теже. |
На |
рис. |
46 |
|
показана |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
задача на определение рас- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
стояния между двумя парал- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
лельными |
прямыми |
общего |
|||||||||
|
|
|
|
|
|
|
|
|
|
положения. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Методом введения но- |
|||||||
|
|
|
|
|
|
|
|
|
|
вых |
плоскостей |
проекций |
|||||||||
|
|
|
|
|
|
|
|
|
|
добиваемся |
вырождения |
||||||||||
|
|
|
|
|
|
|
|
|
Рис. 46 |
проекций прямых в точки. |
|||||||||||
|
|
|
|
|
|
|
|
|
Расстояние между |
этими |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
точками является искомым.
50
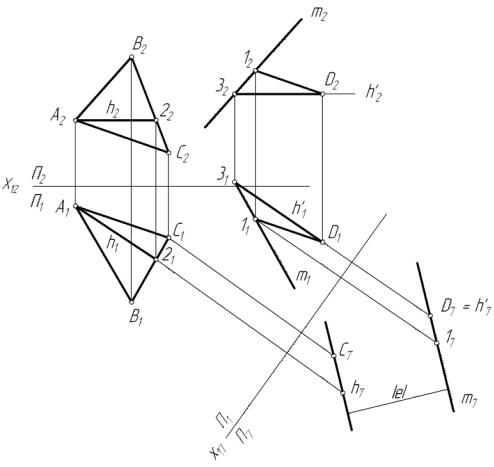
Наконец, на рис. 47 показана задача на определение истинного расстояния между параллельными плоскостями общего положения. Плоскости заданы: одна – тремя точками А, В, С , а другая – прямой m и точкой D. Параллельность исходных плоскостей подтверждается параллельностью пересекающихся прямых АВ ∩ АС одной плоскости, пересекающимся прямым m ∩ ( D, 1 ) другой плоскости. Для решения задачи выбираем новую плоскость проекций П7 , перпендикулярную исходным плоскостям. Для этого выбираем ось Х17 , перпендикулярную горизонтальной проекции А1 , 21 горизонтали плоскости А, В, С. В результате проецирования исходных плоскостей на плоскость П7 они, являясь проецирующими по отношению к этой плоскости проекций, вырождаются в прямые линии. Расстояние между этими прямыми, измеряемое общим к ним перпендикуляром, является искомым расстоянием /е / между исходными плоскостями.
Рис. 47
Во всех приведенных задачах мы занимались восстановлением величин параметров формы и положения исходных фигур, которые на исходных чертежах были заданы с искажением либо не заданы вообще.
Однако имеются задачи, которые мы условно назовём комплексными. Эти задачи часто имеют как метрические, так и позиционные разделы в процессах решений. Они отличаются тем, что параметры формы и поло-
51
жения фигур заданы в исходных данных и требуется построить соответствующие этим параметрам и геометрическим условиям проекции фигур.
На рис. 48-50 приведены примеры таких задач.
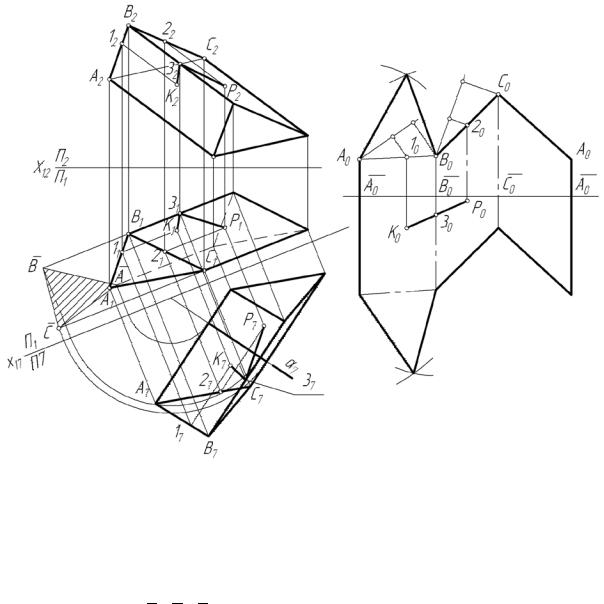
На рис. 48 задана треугольная призма проекциями на плоскостях П1 и П2 . На гранях А В В’ А’ и В С С’ В’ призмы заданы точки К и Р соответственно. Требуется построить кратчайший путь между точками К и Р по граням призмы. Известно, что кратчайшее расстояние между точками измеряется по прямой. Такую прямую, которая соединит точки К и Р, мы можем построить на развертке призмы, поскольку грани призмы будут лежать в одной плоскости. Кратчайший путь, в нашем случае, будет задан тремя точками: К, Р и точкой на ребре, разделяющем грани, в которых заданы точки.
Рис. 48
Для построения развертки призмы построена её проекция на плоскость П7 , параллельную ребрам призмы. На дополнительной плоскости задана горизонтально проецирующая плоскость α своим следом α7 , перпендикулярная ребрам призмы (нормальное сечение призмы). Вращением α7 до совмещения с плоскостью П 1 (как показано на рис. 48) получена ис-
тинная величина А , В , С нормального сечения. При построении развертки строится развернутое нормальное сечение, которое используется как ось
52

координат для построения ребер призмы. Истинная величина ребер берется с проекции призмы на П 7 . К 0 и Р 0 точки К и Р на развертке. Точка 3 0 построена при соединении точек К0 и Р0 прямой. Переносим точку 3 0 на проекции призмы, получим проекции 3 1 и 3 2 . Соединяя их на исходном чертеже с проекциями точек К и Р, получим проекции кратчайшего пути между точками К и Р.
Продолжая тему разверток, заметим, что, как было указано выше, поверхности, состоящие из эллиптических либо гиперболических точек, развернуть нельзя. На практике строят условные развертки таких поверхностей. Для этого неразвертывающуюся поверхность замещают кусками развертывающихся поверхностей. Затем каждый кусок (отсек) развертывающейся поверхности заменяют гранной поверхностью. Последнюю развертывают как было указано на рис. 48.
Рис. 49
На рис. 49 приведены исходные проекции полусферы. Для построения условной развертки исходная поверхность заменяется (аппроксимируется) кусками цилиндра вращения, касающегося полусферы. Показан один из восьми отсеков аппроксимирующего цилиндра (одна из образующих отсека – l касается очерковой окружности горизонтальной проекции полусферы). Отсек цилиндра аппроксимируется поверхностью призмы, ребра которой 0, 1, 2, 3, 4 показаны на рис. 49. В правой части рис. 49 показана развертка призмы по информации, взятой с исходных проекций отсека. Та-
53

ким образом, в условную развертку полусферы войдут восемь отсеков аппроксимирующих фигур, что и указано на рис. 49.
На рис. 50 даны исходные проекции фигуры, в состав которой вошли: сфера, цилиндры вращения и конус вращения. Задана также плоскость α общего положения (тремя точками А, В, С ), пересекающая фигуру. Требуется построить истинную величину сечения фигуры. Исходный чертёж задан по схеме внутренней параметризации фигуры. В ходе решения построена вспомогательная проекция, на которой плоскость сечения вырождается в след α7 . Для этого на исходном чертеже задаём горизонталь (А, 1 ) и положение системы координат, параметризующей исходную фигуру, выбираем из условия: 07 , Х7 А1 , 11 , как показано на рис. 50.
Для построения истинной величины фигуры сечения выбираем в
плоскости α вспомогательную систему параметризации X 0 Y , в которой измеряются параметры формы сечения. На рис. 50 достаточно построить горизонтальную Х1 , 01 , Y1 и вспомогательную Х7 , 07 , Y7 проекции вспомогательной системы параметризации. Теперь истинное по форме и величине сечение можно построить, выбирая ординаты со следа α7 , а соот-
Рис. 50
54
