Горизонтальные проекции этих точек построены из условия инцидентности горизонтальным проекциям горизонталей.

Рис. 26

3.1. Задачи на построение пересечений фигур

Рассмотрим теперь задачи на построение пересечений фигур. Эти задачи являются, по сути, некоторым обобщением задач на построение инциденций. Фигуры, получающиеся в результате пересечения двух исходных фигур, можно считать инцидентными одновременно двум исходным фигурам. Критерием разрешимости задачи на пересечение фигур является наличие двух проекций исходных фигур. Эта задача является позиционной. Здесь также можно сформулировать две основные задачи: построения фигур пересечения и распознавание факта пересечения исходных фигур.

Признак пересечения двух прямых на чертеже прост: одноимённые проекции прямых должны пересекаться в точках, лежащих на одной линии связи.

На рис. 27, а решена задача построения проекций прямой в, инцидентной точке В (В1 , В2 ) и пересекающей прямую а (а1 , а2 ). Для решения задачи через одну из проекций заданной точки В, например, через фронтальную, проведена произвольная прямая, пересекающая фронтальную проекцию а2 в точке 12 . Затем через точку 12 построена линия связи до

31

пересечения с проекцией а1 прямой а. Горизонтальная проекция искомой прямой определена точками В1 и 11 .

На рис. 27, в показаны скрещивающиеся прямые а и в, проекции которых пересекаются. Точки пересечения проекций реализуются в пространстве парами конкурирующих точек: 1, 2 и 3, 4. Поэтому прямые а и в скрещиваются. Невидимые на проекциях точки в этих парах показаны в скобках.

Наконец, на рис. 27, г показаны пересекающиеся линии, из которых одна линия − кривая. Признак пересечения линий действует и в тех случаях, когда линии кривые.

Включим теперь в рассмотрение плоскости. Здесь наиболее распространенными являются задачи на построение проекции пересечения прямой и плоскости, а также пересечения двух плоскостей.

На рис. 28 показаны различные случаи пересечения прямой с плоскостью. На рис. 28, а задана фронтально-проецирующая плоскость α своим фронтальным следом α2 и пересекающая её прямая а (а1 , а2 ). В данном случае решение является явным, поскольку фронтальная точка пересечения прямой с плоскостью совпадает со следом плоскости. Вторая проекция точки пересечения строится в пересечении линии связи из точки К2 с горизонтальной проекцией прямой а .

На рис. 28, б задана прямая а (а 1 , а 2 ) и построены проекции пересечения этой прямой с плоскостями проекций П1 и П2 (следы прямой). Для решения задачи проекции прямой продолжены до пересечения с осью 0Х в точках M2 и N1 , из которых восстановлены линии связи до пересечения с

32

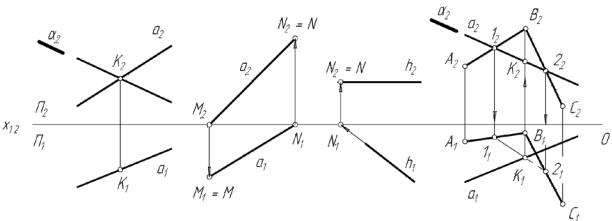
проекциями прямой в точках M1 = М и N2 = N. Знак равенства в этих выражениях означает, что с точкой М1 совпадает горизонтальный след М, а с точкой

N2 − фронтальный след прямой N.

На рис. 28, в показано построение фронтального следа горизонтали

h (h1 , h2 ), горизонтальный след отсутствует вследствие параллельности горизонтали плоскости x0y. Подобным образом может быть построен след фронтали.

Наконец, на рис. 28, г показан общий случай построения проекций точки пересечения прямой с плоскостью общего положения. Плоскость задана проекциями своего определителя: тремя точками А, В, C. С целью р е- шения задачи введём фронтально-проецирующую плоскость α (α2 ). Соединим точки А, В и В, С в исходной плоскости отрезками прямых. Построим проекции линии пересечения плоскости α и АВС. В этом случае решение

Рис. 28

Изложенная последовательность операций отличается тем, что она действительна и в тех случаях, когда вместо плоскостей задаются кривые поверхности. Введенная плоскость α называется посредником.

На рис. 29 показаны задачи, связанные с построением на чертеже проекций линии пересечения плоскостей. На рис. 29, а плоскость задана пересекающимися прямыми а и h, из которых h является горизонталью плоскости. Требуется построить линии пересечения плоскости с плоскостями координат хОу и xОz. Для решения построены следы прямых а и h, через которые очевидно пройдут искомые следы плоскости. Эти следы α1

33

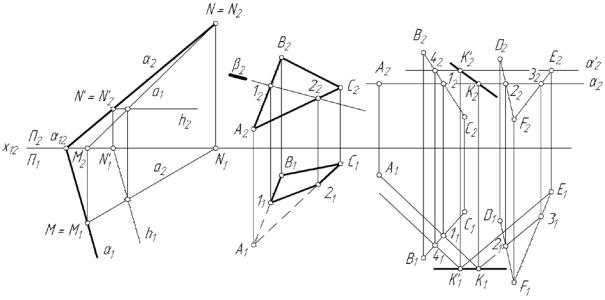
и α2 пересекаются на оси Ох в точке α 1 2 , называемой точкой схода сле-

дов. Проекция горизонтали h1 || α1 . Все сказанное нетрудно доказать, рассматривая ситуацию в пространстве. Вместо прямой общего положения можно было бы задать фронталь f плоскости и тогда f2 α2 .

На рис. 29, б показана задача построения проекций линии пересече-

ния двух плоскостей, из которых одна − проецирующая. Подобную задачу мы решали, рассматривая рис. 28.

Рис. 29

Наконец, на рис. 29, в решена задача на построение проекций линии пересечения двух плоскостей общего положения. Плоскости заданы определителями, в которые входят тройки точек: АВС в одной и DЕF в другой плоскости. Для решения задачи годится последовательность операций, которую мы применили для построения проекций точки пересечения прямой с плоскостью общего положения. Во-первых, вводим посредник − горизонтальную плоскость α (α2 ). Во-вторых, построим проекции линий пересечения А, 1 и 2, 3 исходных плоскостей с плоскостьюпосредником. Поскольку эти линии лежат в одной плоскости α, то они пересекаются в точке К (К1 , К2 ). Эта точка лежит на линии пересечения плоскостей АВС и EDF. Для построения второй точки линии пересечения повторяем все операции, начиная с введения второй плоскости-посредника α'

(α'2 ). Полученная вторая точка К' (K'1 , K'2 ) позволяет определить искомую линию пересечения двух плоскостей. На рис. 29, в проекции этой линии показаны утолщённой линией.

Изложенный способ решения позиционной задачи называют спосо-

бом введения посредника.

34

Рассмотрим применение этого способа в задачах с участием поверхностей. После введения посредника приходится строить пересечения его с исходными фигурами. В случае прямых и плоскостей такие пересечения ограничивались точками либо прямыми. Если же в задаче исходными являются кривые поверхности, то выбор посредника не всегда прост. Желательно выбрать такой посредник, линии пересечения которого с исходными поверхностями просты для построения.

Примеры решения задачи на построение линии пересечения плоскости с поверхностью приведены на рис. 30. Здесь в качестве исходных выбраны проецирующие плоскости. Общие случаи сводятся к этим путем применения преобразований проекций. Эти случаи разобраны в разделе «методы преобразования чертежей».

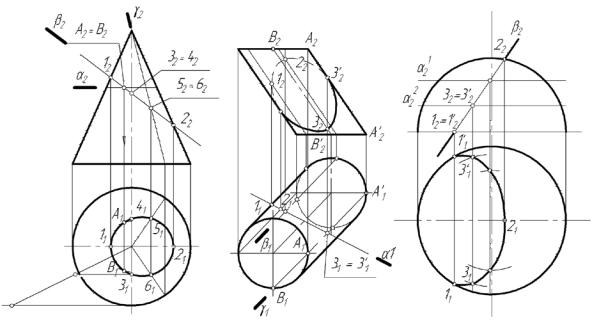
На рис. 30, а фронтально-проецирующая плоскость β, заданная сле-

дом β2 , пересекает конус вращения. В качестве плоскостей-посредников можно выбрать плоскости, перпендикулярные оси поверхности, пересекающие поверхность по окружностям. На рис. 30, а показан след α2 такой плоскости. Результат пересечения: точки А и В лежат на искомой линии, для построения которой необходимо ввести ряд плоскостей-посредников, параллельных α .

Рис. 30

В рассматриваемом примере возможно также применение плоско- стей-посредников, проходящих через вершину конуса. На рис. 30, а показан след γ2 такой фронтально-проецирующей плоскости, пересекающей ко-

35

нус по двум образующим. В результате пересечения исходной плоскости β и посредника γ получены проекции точек 5 и 6.

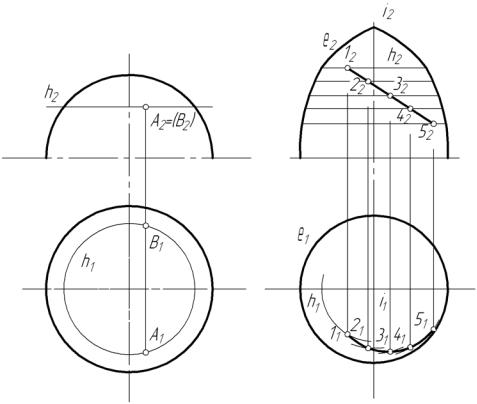
Важно отметить, что при рассмотрении исходных данных можно отметить точки, для построения которых не нужны операции с посредником. Примером являются точки 1 и 2 на чертеже рис. 30, а. Эти точки инцидентны фронтальным очерковым образующим конуса, поэтому на фронтальной проекции их надо только поименовать: 12 и 22 . Горизонтальные проекции этих точек лежат на соответствующих проекциях очерковых образующих, которые совпадают с центровой горизонтальной линией конуса. Точки 3 и 4, лежащие в плоскости γ, проходящей через ось конуса, могут быть построены пропорциональным делением соответствующей образующей на горизонтальной проекции конуса в том же отношении, в котором проекции точек 3 и 4 делят фронтальную проекцию образующей. На рис. 30, а таким построением найдена проекция 31 точки 3. Проекция точки 4 построена из соображений симметричности 41 относительно горизонтальной центровой линии с точкой 31 .

Таким же способом на рис. 30, б построены проекции линии пересечения наклонного кругового цилиндра с плоскостью α, заданной своим горизонтальным следом. Здесь плоскостями-посредниками выбраны гори- зонтально-проецирующие плоскости γ, β ,…, заданные своими горизонтальными следами γ1 , β1 , ... . Эти следы пересекают проекции оснований цилиндра, например, в точках А1 и В1 , через которые проходят образующие, являющиеся результатом пересечения плоскости-посредника с цилиндром. Образующие пересекают след исходной плоскости в точках

же, как и в предыдущем примере, можно отметить точки, которые строятся непосредственно.

В дальнейшем точки, которые в задачах на пересечение строятся непосредственно, будем называть опорными. В ряде случаев с них полезно начинать решение задачи.

На рис. 30, в показаны проекции половины сферы и задана фрон- тально-проецирующая плоскость β фронтальным следом β2 . В этой задаче

опорными точками искомой линии пересечения полусферы с плоскостью β являются точки, инцидентные плоскости, которая отсекает половину сферы, это точки 1 и 1′. Их проекции отмечаются без всяких построений – непосредственно. Опорной является также точка 2, её фронтальная проекция инцидентна фронтальному очерку полусферы. Проекции этой точки находятся также непосредственно.

36

Произвольная точка искомой линии пересечения строится с помощью фронтально-проецирующих и параллельных плоскости xОy плоско- стей-посредников α . Две такие плоскости показаны на рис. 30, в. Построение с помощью этих плоскостей точек, инцидентных искомой линии пересечения, понятно из чертежа.

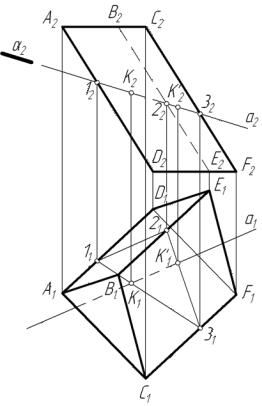
На рис. 31-33 рассмотрены задачи на построение точек пересечения

щий проекцию а1 в точках К1 и К'1 .

Эти точки являются горизонтальными проекциями искомых точек пересечения прямой а с поверхностью исходной призмы. Фронтальные проекции К2 , К'2 находятся с помощью линий связи.

На рис. 32-33 показаны задачи на построение пересечений прямых с поверхностями конуса и наклонного цилиндра. Эти задачи можно решать также с помощью плоскостей-посредников, проведенных через исходные прямые, пересекающие поверхность. Однако в этом случае приходится строить достаточно сложные проекции линий пересечения посредников с исходными поверхностями (см. рис. 30).

37

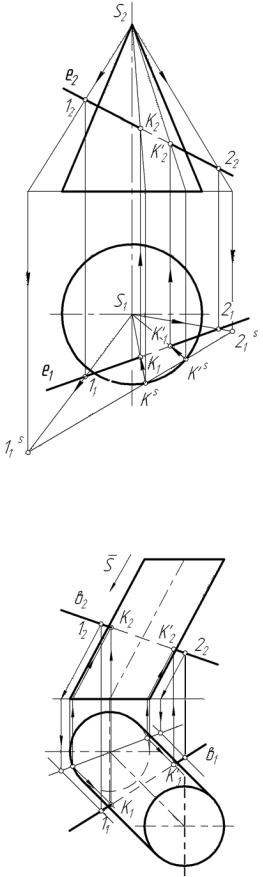
Поэтому эти задачи целесообразно решать с помощью построения дополнительных проекций исходных фигур на специально выбранную плоскость. В случае исходного конуса выбирается центральное вспомогательное проецирование на плоскость основания конуса с центром проекций в точке S (S1 , S2 ) − вершине конуса. Центральной проекцией конуса на плоскость его основания является окружность основания, имеющаяся на исходном чертеже. Для построения центральной проекции исходной прямой ℓ (ℓ1 , ℓ2) выбираем на ней две произвольные точки 1 и 2 . Эти точки проецируем из центра S на плоскость основания конуса. На рис. 32 и рис. 33 эти построения показаны стрелками. Проекция прямой 11 S , 21 S является

Рис. 32 вспомогательной проекцией исходной прямой на плоскость основания конуса. Точки K S и К' S являются центральными проекциями искомых точек.

Горизонтальные и фронтальные проекций этих точек получены обратным по направлению проецированием точек K S и К' S. Эти построения показаны стрелками.

На рис. 33 показана задача на построение пересечения прямой в (в1, в2) c поверхностью наклонного цилиндра.

Отличием примененного здесь метода является параллельное проецирование исходных фигур на плос-

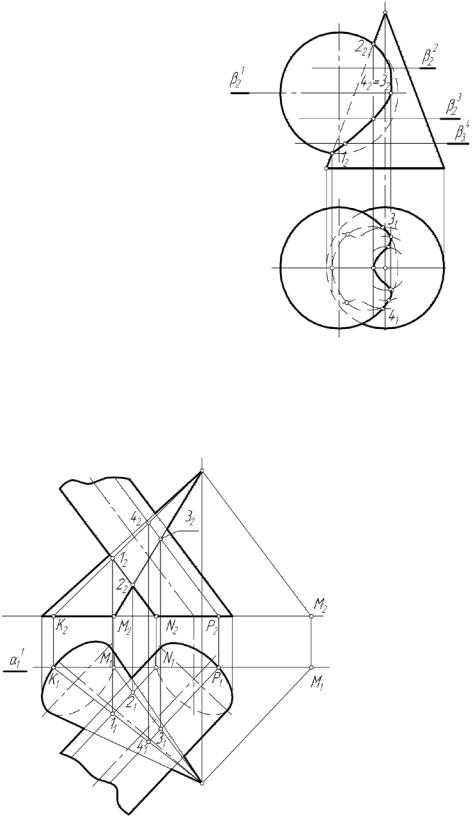
стью цилиндра.

На рис. 34-36 показаны примеры решения задач на построение проекций линий пересечения поверхностей с применением различных посредников.

На рис. 34 выбран посредник в виде горизонтальной фронтально про-

формы оснований цилиндра и конуса эти плоскости пересекают исходные поверхности по парам образующих прямых линий. На схематическом чертеже (рис. 35) показано построение одной из плоскостей-посредников. Для

Рис. 35

39

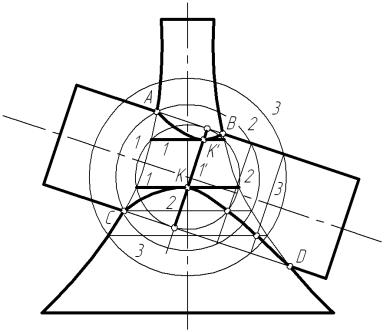
этого через вершину конуса проведена прямая, параллельная образующим цилиндра. Построен горизонтальный след М (М1 , М2 ) этой прямой. Все остальные плоскости-посредники будут иметь горизонтальные следы, проходящие через точку М1 . На рис. 35 показана одна такая плоскость α 1. Её след α 11 пересекает основания исходных фигур в точках К1 , М'1 , N1 и Р1

. Точки пересечения образующих цилиндра и конуса, проходящих через эти точки, образуют четверку точек 1, 2, 3, 4, принадлежащих искомой линии пересечения.

Обратим внимание на высокую эффективность этого способа: введение одного посредника влечёт за собой получение четырех точек, принадлежащих линии пересечения. В случае, показанном на рис. 34, мы получали пару точек.

Наконец, на рис. 36 приведен пример применения в качестве посредника концентрических сфер. Применение этого способа ограничено случаями, когда пересекаются поверхности вращения с пересекающимися осями. Причем плоскость пересекающихся осей параллельна плоскости проекций. При этих ограничениях сфера пересекается с поверхностью вращения по окружности, которая проецируется на упомянутую плоскость проекций в виде прямой. Сферы посредники задаются с центром в точке пересечения осей поверхностей. Строятся линии пересечения сферы с исходными поверхностями. Пересечение этих линий дают проекции искомых точек, лежащих на линии пересечения. Например, на рис. 36 сфера 1 дает пересечения 1, 1 ', которые дают точки К и К ’. При введенных в этой задаче ограничениях горизонтальная проекция может отсутствовать.

Рис. 36

40