
- •Глава 3. Теория пределов
- •§ 3.1. Предел последовательности. Предел функции
- •§ 3.2. Бесконечно малые величины
- •§ 3.3. Арифметические свойства предела
- •§ 3.4. Предельный переход в неравенствах
- •§ 3.5. Односторонние пределы. Пределы при стремлении к бесконечности
- •§ 3.6.Первый замечательный предел
- •§ 3.7. Предел монотонной ограниченной функции
- •§ 3.8. Число e Теорема 3.8.1. Существует предел последовательности .
- •§ 3.9. Критерий Коши существования предела последовательности, предела функции
§ 3.2. Бесконечно малые величины
Определение
3.2.1. Последовательность
 называется
бесконечно
малой,
если
называется
бесконечно
малой,
если
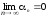 .
Аналогично, функция
.
Аналогично, функция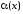 -
бесконечно
малая
при
-
бесконечно
малая
при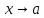 ,
если
,
если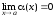 .
.
Теорема
3.2.1. Предел
последовательности
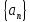 существует и равен числу А
тогда
и только тогда, когда
существует и равен числу А
тогда
и только тогда, когда
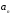 можно
представить в виде
можно
представить в виде
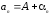 ,
где
,
где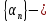 бесконечно малая последовательность.
бесконечно малая последовательность.
Аналогично,
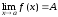 тогда и только тогда, когда
тогда и только тогда, когда
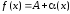 ,
где
,
где
 -
бесконечно малая при
-
бесконечно малая при
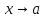 функция.
функция.
Доказательство.
Проведем его для случая функций. Для
предела последовательности оно вполне
аналогично. Итак, обозначим
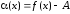 .
Условие
.
Условие
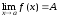 равносильно тому, что
равносильно тому, что
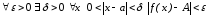 ,
что равносильно условию
,
что равносильно условию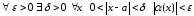 ,
что, в свою очередь, означает, что
,
что, в свою очередь, означает, что
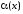 -
бесконечно малая при
-
бесконечно малая при
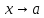 .
.
Определение
3.2.2. Функция
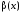 называется ограниченной
при
называется ограниченной
при
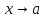 ,
если она ограничена в некоторой проколотой
окрестности
,
если она ограничена в некоторой проколотой
окрестности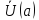 , т.е. если существует такое число
, т.е. если существует такое число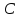 , что для всех из окрестности
, что для всех из окрестности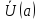 выполнено
неравенство
выполнено
неравенство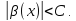 В
виде логических формул это выглядит
так:
В
виде логических формул это выглядит
так: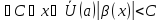 .
.
Теорема 3.2.2. (Свойства бесконечно малых)
Если
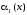 и
и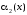 -
бесконечно малые при
-
бесконечно малые при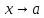 ,
то алгебраическая сумма -
,
то алгебраическая сумма -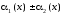 тоже
бесконечно малая при
тоже
бесконечно малая при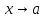 ;
;
Если
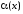 -
бесконечно малая и
-
бесконечно малая и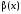 -
ограниченная при
-
ограниченная при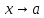 ,
то произведение
,
то произведение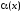
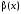 есть бесконечно малая при
есть бесконечно малая при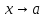 ;
;
Если
 и
и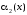 - бесконечно малые при
- бесконечно малые при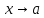 ,
то произведение
,
то произведение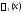
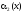 -
тоже бесконечно малая при
-
тоже бесконечно малая при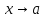 .
.
Бесконечно малые последовательности обладают вполне аналогичными свойствами:
Если
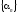 и
и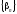 -
бесконечно малые последовательности,
то алгебраическая сумма -
-
бесконечно малые последовательности,
то алгебраическая сумма -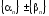 тоже
бесконечно малая последовательность;
тоже
бесконечно малая последовательность;
Если
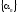 -
бесконечно малая последовательность,
а
-
бесконечно малая последовательность,
а - ограниченная последовательность
(т.е.
- ограниченная последовательность
(т.е.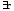 :
:
 ), то
), то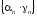 - бесконечно малая последовательность;
- бесконечно малая последовательность;Если
 и
и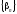 -
бесконечно малые последовательности,
то произведение
-
бесконечно малые последовательности,
то произведение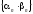 -
бесконечно малая последовательность.
-
бесконечно малая последовательность.
Доказательство проводим для случая бесконечно малых функций.
Зафиксируем произвольное
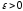 и рассмотрим
число
и рассмотрим
число
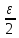 .
Тогда, по определению предела, справедливы
утверждения: существует число
.
Тогда, по определению предела, справедливы
утверждения: существует число
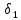 такое, что из неравенств
такое, что из неравенств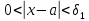 следует неравенство
следует неравенство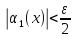 и существует число
и существует число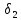 такое, что из неравенств
такое, что из неравенств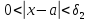 следует неравенство
следует неравенство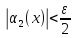 .
Пусть
.
Пусть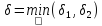 .
Тогда из неравенств
.
Тогда из неравенств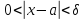 вытекают неравенства
вытекают неравенства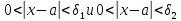 ,
из которых следуют неравенства
,
из которых следуют неравенства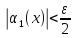 и
и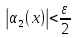 .Следовательно,
при
.Следовательно,
при
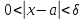 имеют место неравенства
имеют место неравенства
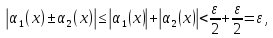
означающие справедливость первого утверждения теоремы.
Пусть
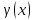 ограничена
при
ограничена
при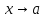 ,
т.е. в некоторой проколотой окрестности
,
т.е. в некоторой проколотой окрестности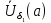 с некоторой постоянной
с некоторой постоянной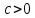 для любого
для любого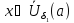 выполняется неравенство
выполняется неравенство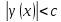 .
Зафиксируем произвольное
.
Зафиксируем произвольное
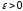 и рассмотрим
число
и рассмотрим
число
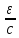 .
Тогда существует такое число
.
Тогда существует такое число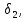 что из неравенств
что из неравенств
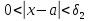 вытекает неравенство
вытекает неравенство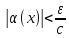 . Пусть
. Пусть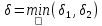 .
Тогда из неравенств
.
Тогда из неравенств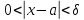 вытекают неравенства
вытекают неравенства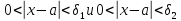 ,
из которых следуют неравенства
,
из которых следуют неравенства и
и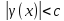 .
Следовательно, при
.
Следовательно, при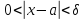 имеем:
имеем: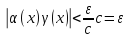 .
.Сначала докажем лемму.
Лемма
3.2.1. Если
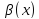 -
бесконечно малая при
-
бесконечно малая при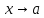 ,
то она
,
то она
ограничена
при
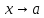 .
(Обратное
утверждение неверно!).
.
(Обратное
утверждение неверно!).
Доказательство:
возьмем
 и
получим, чтосуществует
число
и
получим, чтосуществует
число такое, что для всех
такое, что для всех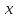 из
из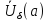 выполнено
неравенство
выполнено
неравенство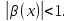 . Это означает, что
. Это означает, что
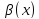 ограничена
при
ограничена
при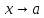 .
Лемма доказана.
.
Лемма доказана.
Вернёмся
к теореме. По доказанной лемме
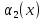 ограничена при
ограничена при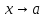 .
Осталось применить свойство 2) бесконечно
малых, доказанное выше.
.
Осталось применить свойство 2) бесконечно
малых, доказанное выше.
§ 3.3. Арифметические свойства предела
Теорема 3.3.1. (Арифметические свойства предела)
Пусть
две функции
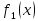 и
и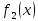 ,
имеют при
,
имеют при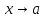 ,
соответственно, пределы
,
соответственно, пределы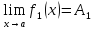 и
и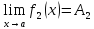 .
Тогда предел суммы, разности, произведения,
и, если
.
Тогда предел суммы, разности, произведения,
и, если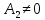 ,
частного этих функций равны соответственно
сумме, разности, произведению и частному
значений этих пределов, т.е.
,
частного этих функций равны соответственно
сумме, разности, произведению и частному
значений этих пределов, т.е.
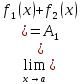
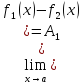
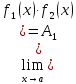
а
если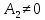 , то
, то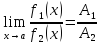 .
.
Аналогичная
теорема верна и для последовательностей.
Если
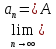 ,
,
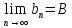 ,
то
,
то
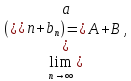
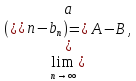
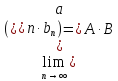 ,
,
а
если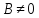 ,
то и
,
то и

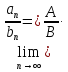
Доказательство. По теореме 3.2.1 из условия следует, что
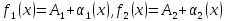 ,
,
где
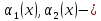 бесконечно малые при
бесконечно малые при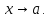 Тогда
Тогда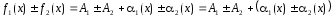 .
.
По
теореме 3.2.2
алгебраическая сумма бесконечно малых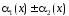 - бесконечно малая, т.е.
- бесконечно малая, т.е.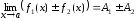 ,
по теореме 3.2.1.
,
по теореме 3.2.1.
Перейдем к произведению
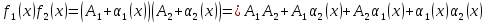
Последние
три слагаемых - бесконечно малая величина
при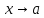 по свойствам 2 и 3 бесконечно малых. По
свойству 1 их сумма – бесконечно малая
при
по свойствам 2 и 3 бесконечно малых. По
свойству 1 их сумма – бесконечно малая
при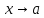 . По теореме3.2.1,
. По теореме3.2.1,
 .
.
Перейдем к пределу частного и докажем сначала лемму:
Лемма
3.3.1. Если
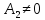 ,
то существует число
,
то существует число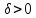 такое,
что для всех
такое,
что для всех
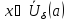 выполняется
неравенство
выполняется
неравенство
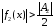 .
.
Доказательство.
Выберем
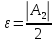 .
Тогда, так как
.
Тогда, так как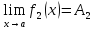 ,
существует
число
,
существует
число
 такое,
что для всех
такое,
что для всех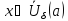 выполняется
неравенство
выполняется
неравенство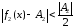 .
Следовательно,
.
Следовательно,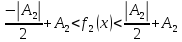
и
при любом знаке числа
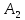 выполняется неравенство
выполняется неравенство
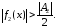
Лемма доказана.
Теперь докажем следующее утверждение:
Лемма
3.3.2. Если
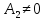 , то
, то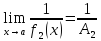 .
.
Доказательство. Имеет место равенство
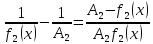 =
=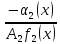 .
.
По
лемме 3.3.1 в
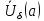 выполняется
неравенство
выполняется
неравенство
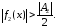 Следовательно,
Следовательно,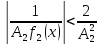 . Значит, функция
. Значит, функция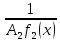 ограничена
при
ограничена
при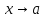 ,
и
,
и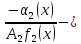 бесконечно малая при
бесконечно малая при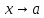 .
Таким образом,разность
.
Таким образом,разность
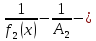 бесконечно
малая, т.е.
бесконечно
малая, т.е.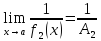 . Лемма доказана.
. Лемма доказана.
Для
доказательства равенства
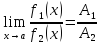 применим
лемму 3.3.2 и часть теоремы 3.3.1 о пределе
произведения функций..
применим
лемму 3.3.2 и часть теоремы 3.3.1 о пределе
произведения функций..
