10. Экстремальные задачи теории графов: задача о кратчайшем пути, алгоритм Дейкстры.

Определение. Графом G называется пара (V, E), где 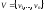– непустое множество вершин графа, а– множество ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.

Определение. Если задача состоит в том, чтобы найти экстремум (максимум или минимум) определенной функции от этих значений, то её принято называть экстремальной задачей.

Задача о кратчайшем пути - поиск кратчайшего пути между двумя вершинами в предположении, что каждое ребро графа имеет определенную длину. Например, пусть имеется сеть до­рог, соединяющих несколько населенных пунктов. Часто возникает задача найти такой путь для перевозки груза из пункта А в пункт В через другие промежуточные пункты, чтобы суммарная длина дорог, составляющих этот путь, была минимальна. Иногда требуется, чтобы такой путь обеспечивал минимальное время или минимальные затраты на перевозку груза из А в В. Всё это разные варианты задачи о крат­чайшем пути. Схема алгоритма Дейкстры для решения задачи о кратчайшем пути такова:

1. найти вершину и₁, ближайшую к вершине и₀ (выбирается кратчайшее ребро, инцидентное вершине и₀);

2. пусть уже найдены k самых близких к и₀ вершин и₁, и₂,…, и_k и известны величины d(и₁), d(и₂),…, d(и_k) – их удаленности от вершины и₀ (причем d(и₁) ≤ d(и₂) ≤ … ≤ d(и_k)); тогда для каждой вершины и из множества V \{и₀, и₁, и₂,…, и_k} вычислить параметр D(и), задаваемый равенством D(и) = min{d(и_i) + l (u_i, u)},

3. где минимум берется по i = 0, 1, 2,…, k, а l (u_i, u) – длина ребра [u_i, u];

4. следующая вершина и_k+1 – ближайшая к и₀ среди всех вершин из множества V \{и₀, и₁, и₂,…, и_k} – находится из условия D(и_k+1) = min{D(и)}, где минимум ищется по всем вершинам и из множества V \{и₀, и₁, и₂,…, и_k};

5. положить d(и_k+1) = D(и_k+1).

Шаги 2 – 4 повторяются в цикле по k = 1, 2, 3,…, n – 1.

11. Изоморфизм и гомеоморфизм графов, методы доказательства изоморфности и неизоморфности графов.

Определение. Графом G называется пара (V, E), где 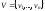– непустое множество вершин графа, а– множество ребер графа, причем каждое ребро – это неупорядоченная пара различных вершин.

Всякий граф можно изобразить на плоскости в виде точек и непрерывных линий, соединяющих эти точки. При этом один и тот же граф может иметь бесконечно много различных изображений (укладок графа на плоскости).

Определение. Говорят, что взаимно однозначное соответствие между множествами вершин двух графов сохраняет смежность вершин, если любой паре смежных вершин первого графа соответствует пара смежных вершин второго.

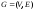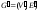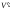Определение. Два графа иназываютсяизо­морфными, если существует взаимно однозначное соответствие между множествами вершин и, которое сохраняет смежность вершин.

Чтобы доказать, что два графа не изоморфны, надо найти какую-либо характеристику этих графов, по которой они различаются. Для графов сложной структуры с большим количеством вершин и ребер подобрать такую характеристику иногда бывает очень трудно. Поэтому проблема изоморфизма считается одной из самых сложных в теории графов.

Также установить изоморфизм двух графов можно и с помощью их матриц смежности. Для этого надо одну матрицу преобразовать в другую одновременной перестановкой некоторых её строк и столбцов. Однако если заранее не известно, изоморфны ли данные графы, такой способ проверки изоморфизма, так же как и перебор всех возможных вариантов взаимно однозначного соответствия между вершинами графов, требует большого объема вычислений.

Определение. Два графа называются гомеоморфными, если их можно получить из одного графа с помощью однократного или многократного применения операции подразбиения ребра.