
- •1. Основные понятия теории графов, удаленность вершины, центр, радиус и диаметр графа.
- •2. Способы задания графов, свойства матриц смежности и инциденций, теорема о рукопожатиях.
- •3. Основные операции над графами, неравенства для числа вершин, ребер и компонент связности графа.
- •4. Типы графов, дополнительные графы, двудольные графы, критерий двудольности.
- •5. Обходы графов: эйлеровы цепи и циклы, необходимые и достаточные условия их существования, алгоритм Флери.
- •6. Обходы графов: гамильтоновы цепи и циклы, достаточные условия их существования.
- •7. Деревья, их свойства, кодирование деревьев, остовные деревья.
- •8. Экстремальные задачи теории графов: минимальное остовное дерево, алгоритмы Прима и Краскала.
- •9. Экстремальные задачи теории графов: задача коммивояжера, «жадный» алгоритм
- •10. Экстремальные задачи теории графов: задача о кратчайшем пути, алгоритм Дейкстры.
- •11. Изоморфизм и гомеоморфизм графов, методы доказательства изоморфности и неизоморфности графов.
- •12. Плоские укладки графов, планарные графы, критерий Понтрягина-Куратовского.
- •13. Необходимые условия планарности, формула Эйлера для планарных графов.
- •14. Правильные вершинные раскраски графов, хроматическое число, неравенства для хроматического числа.
- •15. Теорема о пяти красках, гипотеза четырех красок, «жадный» алгоритм.
- •16. Хроматический многочлен, его нахождение и свойства.
- •17. Задача о поиске выхода из лабиринта, реберная раскраска графа.
- •18. Ориентированные графы, источники и стоки, топологическая сортировка, алгоритм Демукрона.
- •19. Составление расписания выполнения комплекса работ в кратчайшие сроки методами теории графов.
- •20. Элементарные булевы функции и способы их задания (табличный, векторный, формульный, графический, карта Карно).
- •21. Существенные и фиктивные переменные булевых функций, основные тождества, эквивалентные преобразования формул.
- •22. Линейные и нелинейные полиномы Жегалкина, разложение булевых функций в полином Жегалкина методом неопределенных коэффициентов.
- •23. Линейные и нелинейные полиномы Жегалкина, разложение булевых функций в полином Жегалкина методом эквивалентных преобразований.
- •24. Разложение булевых функций в сднф и скнф.
- •25. Минимизация днф и кнф методом эквивалентных преобразований.
- •26. Минимизация днф и кнф с помощью карт Карно.
- •27. Замкнутые классы булевых функций т0, т1, l, лемма о нелинейной функции.
- •28. Замкнутые классы булевых функций s и м, леммы о несамодвойственной и немонотонной функции.
- •29. Полная система функций, теорема о двух системах булевых функций.
- •30. Теорема Поста о полноте системы булевых функций, алгоритм проверки системы на полноту, базис.
- •31. Схемы из функциональных элементов, правила построения и функционирования, метод синтеза сфэ, основанный на сднф и скнф.
- •32. Метод синтеза сфэ, основанный на компактной реализации всех конъюнкций с помощью универсального многополюсника, сложность получаемых схем.
- •33. Основные комбинаторные операции, сочетания и размещения (с возвращением и без возвращения элементов).
- •34. Комбинаторные принципы сложения, умножения, дополнения, включения-исключения.
- •35. Биномиальные коэффициенты, их свойства, бином Ньютона.
- •36. Треугольник Паскаля, полиномиальная формула.
- •37. Алфавитное кодирование: необходимое и достаточные условия однозначности декодирования.
- •38. Алфавитное кодирование: теорема Маркова, алгоритм Маркова.
- •39. Коды с минимальной избыточностью (коды Хаффмана), метод построения.
- •40. Линейные коды, порождающая матрица, двойственный код.
- •41. Самокорректирующиеся коды (коды Хэмминга), метод построения.
- •42. Определение, схема и функционирование абстрактного автомата, способы задания автоматов.
- •43. Типы конечных автоматов, автоматы Мили и Мура, автоматы-генераторы.
- •44. Слова и языки, операции над ними, их свойства.
- •45. Регулярные выражения и регулярные языки, теорема Клини.
- •46. Задача анализа автоматов-распознавателей.
- •47. Задача синтеза автоматов-распознавателей.
- •48. Эквивалентные состояния автомата-распознавателя, эквивалентные автоматы-распознаватели, минимизация автоматов-распознавателей, алгоритм Мили.
- •49. Эквивалентные состояния автомата-преобразователя, эквивалентные автоматы- преобразователи, минимизация автоматов- преобразователей, алгоритм Мили.
- •50. Детерминированные и недетерминированные функции, примеры, способы задания.
- •51. Ограниченно-детерминированные (автоматные) функции, способы их задания.
- •52. Логические автоматы, способы их задания, синтез двоичного сумматора.
- •53. Операции над логическими автоматами: суперпозиция и введение обратной связи.
39. Коды с минимальной избыточностью (коды Хаффмана), метод построения.
Пусть
р1, р2,…, рr– частоты (вероятности), с которыми
буквы алфавита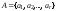 встречаются в исходных сообщениях.
Частоты неотрицательны и удовлетворяют
равенству
встречаются в исходных сообщениях.
Частоты неотрицательны и удовлетворяют
равенству .
.
Определение.
Избыточностью схемы алфавитного
кодирования Σ с длинами кодовых словl1,l2,…,lr
при заданных частотах р1,
р2,…, рrназывается число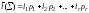 .
.
Избыточность
схемы согласно определению равна
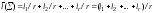 .
.
Пример 1. При заданных частотах р1= 0.4, р2= 0.25, р3= 0.2, р4= 0.15 сравнить избыточность двух схем Σ1и Σ2, где
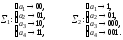
Заметим,
что Σ1– равномерная схема, а Σ2– префиксная, поэтому обе эти схемы
однозначно декодируемы. В схеме Σ1длины кодовых словl1
=l2 =l3
=l4= 2, следовательно,
её избыточность равна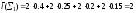 .
.
В
схеме Σ2длины кодовых словl1
= 1,l2 = 2,l3
=l4= 3, поэтому
её избыточность равна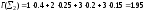 .
.
Пример
2. Для набора частот р1 = 0.4,
р2 = 0.25, р3 = 0.2, р4 =
0.1, р5 = 0.05 требуется построить
суффиксный код Хафмана с исходным
алфавитом и кодирующим алфавитом
и кодирующим алфавитом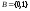 .
.
|
| |||
|
0.4 |
0.4 |
0.4 |
0.6 |
|
0.25 |
0.25 |
0.35 |
0.4 |
|
0.2 |
0.2 |
0.25 |
|
|
0.1 |
0.15 |
|
|
|
0.05 |
|
|
|
Теперь построим бинарное дерево, корень которого располагается в самом верхнем ярусе. Каждая вершина, кроме корня, помечается числом из таблицы. Построение дерева и расстановка пометок его вершин выполняется рекурсивно. Сначала к единственной вершине – корню дерева – добавляются две смежные с ней вершины, которые помечаются числами из последнего столбца таблицы..
Около
каждой концевой вершины дерева указана
частота, а в скобках - соответствующее
ей кодовое слово кода Хафмана. В итоге
получаем префиксную схему Σпкода Хафмана
Однако
по условию задачи требовалось построить
суффиксную схему кодирования. Она легко
получается «зеркальным отражением»
префиксной схемы Σп.Следовательно, искомый суффиксный код
Хафмана задается схемой Σс,
где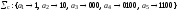 .
.
Избыточность
построенного кода равна
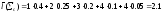
40. Линейные коды, порождающая матрица, двойственный код.
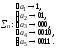
Определение. Коды с кодирующим алфавитом В = {0,1} называются двоичными кодами.
Определение. Булева функция f (x1,x2,…,xn) называется характеристической функцией двоичного кода, если она обращается в единицу на тех и только тех наборах, которые являются кодовыми словами этого кода.
Утверждение.Пусть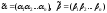 − два кодовых слова двоичного кода Σ.
Через
− два кодовых слова двоичного кода Σ.
Через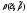 обозначается расстояние Хэмминга между
двумя кодовыми словами
обозначается расстояние Хэмминга между
двумя кодовыми словами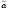 и
и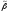 ,
которое вычисляется по формуле
,
которое вычисляется по формуле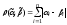 .
Формула означает, что расстояние Хэмминга
между двумя кодовыми словами равно
числу позиций, в которых эти слова
различаются.
.
Формула означает, что расстояние Хэмминга
между двумя кодовыми словами равно
числу позиций, в которых эти слова
различаются.
Определение. Кодовым расстоянием двоичного кода называется минимальное расстояние Хэмминга между двумя его кодовыми словами. Кодовое расстояние схемы Σ – это минимальное число позиций, в которых могут отличаться два её кодовых слова. Геометрическая интерпретация кодового расстояния − это длина кратчайшей цепи, которая соединяет две вершины n-мерного единичного куба, отвечающие кодовым словам данной схемы.
Утверждение.Говорят, что кодовые слова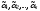 линейно зависимы, если хотя бы одно из
них является линейной комбинацией
остальных слов из этого набора. Если же
ни одно из них не является линейной
комбинацией остальных слов, то они
считаются линейно независимыми.
линейно зависимы, если хотя бы одно из
них является линейной комбинацией
остальных слов из этого набора. Если же
ни одно из них не является линейной
комбинацией остальных слов, то они
считаются линейно независимыми.
Определение. Двоичный код называется линейным кодом, если любая линейная комбинация его кодовых слов также является кодовым словом этого кода.
Из определения линейного кода можно получить следующие его свойства:
Любой линейный код содержит нулевое кодовое слово, т.е. слово, состоящее только из нулей.
Кодовые слова линейного кода обязательно линейно зависимы, так как линейный код всегда содержит нулевое слово, а оно выражается через другие кодовые слова с помощью линейной комбинации вида
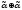 .
.Если линейный код не состоит из одного только нулевого слова, то можно так выбрать несколько его линейно независимых кодовых слов, чтобы все кодовые слова являлись линейными комбинациями выбранных слов.
Линейный код размерности rимеет мощность 2r, т.е. содержит ровно 2rкодовых слов.
Кодовое расстояние линейного кода равно минимальному числу единиц в ненулевом кодовом слове этого кода.
Определение. Порождающей матрицей линейного кода размерности r с длинами кодовых слов, равными n, называется матрица размера r на n, в строках которой стоят базисные кодовые слова этого кода.
Определение.
Кодовые слова
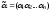 и
и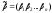 называютсяортогональными,
если
называютсяортогональными,
если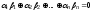 .
Каждое слово ортогонально нулевому
слову. Кроме того, оно может быть
ортогонально и самому себе. Например,
слово (0101) ортогонально словам (0000),
(0010), (1000), (1010), (0101), (0111), (1101) и (1111). Обратим
внимание на то, что эти восемь слов
образуют линейный код.
.
Каждое слово ортогонально нулевому
слову. Кроме того, оно может быть
ортогонально и самому себе. Например,
слово (0101) ортогонально словам (0000),
(0010), (1000), (1010), (0101), (0111), (1101) и (1111). Обратим
внимание на то, что эти восемь слов
образуют линейный код.
Определение. Двойственным кодом к линейному коду Σ называется двоичный код, каждое кодовое слово которого ортогонально любому кодовому слову кода Σ. Двойственный код обладает рядом свойств. Наиболее важное из них состоит в том, что двойственный код к линейному коду размерности r сам является линейным кодом размерности (n – r) , где n – длина кодового слова.
